Download transformer

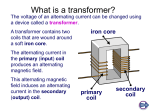
CIRCUITS and
SYSTEMS – part I
Prof. dr hab. Stanisław Osowski
Electrical Engineering (B.Sc.)
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego. Publikacja dystrybuowana jest bezpłatnie
Lecture 5
Magnetically coupled circuits
Phenomena of magnetically coupled coils
A magnetically (inductively) coupled inductor circuit consists of
more than one coil of inductive wire wound on the same magnetic
core.
The flux linkage of the z-turn coil is defined as flux Φ times the
number of turns z. Each coils has its own flux linkage. The total
flux linking each coil is the sum or difference of two compounds:
the leakage flux ψii produced by current through the coil itself and
the mutual flux ψij produced by the current through the other coil j.
For two magnetically coupled coils we have
1  11  12
2  22  21
Self- and mutual inductance
For magnetically coupled coils we have
 1  L1i1  M 12i2
 2   M 21i1  L2 i2
.
• Self-inductances L1, L2
L1 
11
,
i1
L2 
22
i2
• Mutual inductance (M12=M21=M)
M 12 
12

, M 21  21
i2
i1
•Coefficient of coupling k
k
M
L1 L2
Voltage on magnetically coupled coils
The voltage of magnetically coupled coils
d1
di1
di2
u1 
 L1
M
dt
dt
dt
d2
di
di
u2 
 L2 2  M 1
dt
dt
dt
Dot (marking convention)
The self-induced voltage and the mutually induced are additive
(positive coupling) , i.e. have the same polarity if both coil
current enter/leave the dotted or undotted ends of the coils. They
are subtractive (negative coupling), i.e. opposite to each other, if
one coil current enters/leaves the dotted end of the coil while the
other coil current enters/leaves the undotted end of the other coil.
Positive and negative coupling
• Positive coupling
• Negative coupling
Symbolic representation of
magnetically coupled coils
At sinusoidal excitation the symbolic complex form equations are of the
form
U1  jL1 I1  jMI 2
U 2  jL2 I 2  jMI
Sign plus for positive coupling and minus for negative one.
Self inductive reactance of the coil
X L  L
Mutual inductive reactance
X M  M
Voltage over magnetically coupled coils
RMS complex values of voltages across the magnetically coupled
coils
U1  Z L1 I1  Z M I 2  jL1 I1  jMI 2
U 2  Z L 2 I 2  Z M I1  jL2 I 2  jMI 1
ZL1=jω L1, ZL2=jω L2 – the complex self-impedances of the coils
ZM= jω M – the complex mutual inductance of the coils
Elimination of magnetic coupling
Elimination of magnetic couplings is done directly by inspection of
circuits and takes into account only the dot points of coupled coils
(the direction of coil currents has no influence on the elimination).
We recognize two types of couplings:
• coils of identical positions of dots with respect to common node
• coils of reverse positions of dots with respect to common node
Elimination of magnetic coupling (cont.)
• Dots identically situated to the common node
• Dots differently situated to the common node
Rules of elimination of coupling
:
Dots identically situated with respect to the common node
Dots situated in a reverse way with respect to the common node
Example 1
The original circuit with magnetic coupling (a) and after elimination of
couplings (b)
The circuit after elimination of magnetic coupling is
equivalent to the original circuit only with respect to the
currents! The voltages inside the circuits may change.
Example 2
Calculate the currents and voltages of the circuit with magnetic
coupling. Assume: R=5Ω, L1=2H, L2=2H, M=1H, i(t)=5 sin(t+45o)
The circuit after elimination of
coupling
The succeding steps of calculations
• Symbolic values of the circuit elements
5 j 45o
I
e
2
Z1  j L1  M   j1
Z 2  j L2  M   0
Z M  jM  j1
• Input impedance of the circuit
RZ M
1 j 45o
Z

e
R  ZM
2
The succeding steps of calculations (cont.)
• Voltage UAB
U AB  ZI  j5
• Currents
U AB
 j5
R
I1  0
IR 
I2  I3 
U AB
5
ZM
• Voltages of the coupled coils
U L1  jL1 I1  jMI 2  j5
U L2  jL2 I 2  jMI 1  j5
Transformer – principle of operation
A transformer is a device that transfers electrical enegy from
one circuit to another through inductively coupled conductors—
the transformer's coils. A varying current in the first or primary
winding creates a varying magentic flux in the transformer's
core, and thus a varying magnetic field through the secondary
winding. This varying magnetic field induces a varying
electromotive force or voltage in the secondary winding.
The main role of transformer is change the value of voltage
from one level to another one. Change of voltages change also
the levels of currents in both coils.
Transformer – principle of operation
(cont.)
Transmission of energy from primary coil to the secondary one is
done through the magnetic field.
Primary windings
Secondary windings
Illustration of transformer performance
Ideal transformer
Assumptions:
• No losses of power
• Perfect coupling of coils (k=1)
• Turn ratio=voltage ratio
Graphical symbol of ideal transformer
Mathematical relations for ideal
transformer
• Voltage ratio (U1/U2) is equal to the turn ratio (z1/z2)
U1 z1
z

 n  U1  1 U 2  nU 2
U2 z2
z2
• Because of lossless operation we have
U1I1*  U 2 I 2*  I1 
z2
I2
z1
• Matrix description of ideal transformer
U1  n
 I   0
 1  
0  U 
1  2 
I
n   2 
Practical realization of transformer
Practical implementation of transformer is
ferromagnetic core, for which we have (k≈1).
made by using
Electrical model of transformer applying magnetically coupled coils
Mathematical description
• Equations for 2 magnetically coupled coils
U1  jX L1 I1  jX M I 2
U 2   jX L 2 I 2  jX M I1 
• Output voltage
2
XM
 X L1 X L 2  X M
U 2  
U1  jI 2 
X L1
 X L1

• At ideal coupling (k≈1)
2
k 1  XM
 X L1 X L 2
• Output voltage of transformer
XM
U2  
U1
X L1




Voltage and current relations at ideality
Reactances of coils are approximately depending on the number of
turns according to relations
X L1  Kz12 , X L 2  Kz22 , X M  Kz1 z2
K- construction coefficient
At ideal coupling the secondary (output) voltage of transformer is
dependent only on turn ratio.
U 2 I1
z
1

 2 
U1 I 2
z1
n
The minus sign is a result of the assumed directions of voltages and
dot convention.
Example
Calculate the currents in the circuit with ideal transformer at n=2.
Assume: e(t)=14.1sin(t), R=5Ω, C=0.2F.
Solution
Symbolic values of parameters
E  10
j
ZC  
  j5
C
RZ C
Z RC 
 2,5  j 2,5
R  ZC
Circuit description
E  RI 1  U1
U1  nU 2
1
I1  I 2
n
U 2  I 2 Z RC
The numerical results
After subsituting the numerical values we get
I1  0,45  j 0,30
I 2  2 I1  0,90  j 0,60
U 2  Z RC I 2  3,79  j 0,75
U1  2U 2  7,58  j1,5
U2
 0,75  j 0,15
R
U2
I4 
 0,15  j 0,76
ZC
I3 
It is easy to show that
U1
I1 1
 2,

U2
I2 2