* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Class2_7_8_9_frequency_domain
Transmission line loudspeaker wikipedia , lookup
Buck converter wikipedia , lookup
Mains electricity wikipedia , lookup
Opto-isolator wikipedia , lookup
Alternating current wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
History of electric power transmission wikipedia , lookup
Distribution management system wikipedia , lookup
Nominal impedance wikipedia , lookup
Power dividers and directional couplers wikipedia , lookup
Zobel network wikipedia , lookup
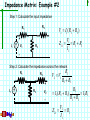
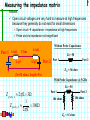
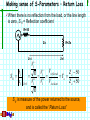
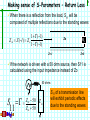
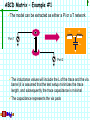
1 Instructor: Richard Mellitz Introduction to Frequency Domain Analysis (3 Classes) Many thanks to Steve Hall, Intel for the use of his slides Reference Reading: Posar Ch 4.5 http://cp.literature.agilent.com/litweb/pdf/5952-1087.pdf Slide content from Stephen Hall Differential Signaling Outline 2 Motivation: Why Use Frequency Domain Analysis 2-Port Network Analysis Theory Impedance and Admittance Matrix Scattering Matrix Transmission (ABCD) Matrix Mason’s Rule Cascading S-Matrices and Voltage Transfer Function Differential (4-port) Scattering Matrix Differential Signaling Motivation: Why Frequency Domain Analysis? Time Domain signals on T-lines lines are hard to analyze Many properties, which can dominate performance, are frequency dependent, and difficult to directly observe in the time domain • Skin effect, Dielectric losses, dispersion, resonance Frequency Domain Analysis allows discrete characterization of a linear network at each frequency Characterization at a single frequency is much easier Frequency Analysis is beneficial for Three reasons Ease and accuracy of measurement at high frequencies Simplified mathematics Allows separation of electrical phenomena (loss, resonance … etc) Differential Signaling 3 Key Concepts 4 Here are the key concepts that you should retain from this class The input impedance & the input reflection coefficient of a transmission line is dependent on: Termination and characteristic impedance Delay Frequency S-Parameters are used to extract electrical parameters Transmission line parameters (R,L,C,G, TD and Zo) can be extracted from S parameters Vias, connectors, socket s-parameters can be used to create equivalent circuits= The behavior of S-parameters can be used to gain intuition of signal integrity problems Differential Signaling Review – Important Concepts The impedance looking into a terminated transmission line changes with frequency and line length The input reflection coefficient looking into a terminated transmission line also changes with frequency and line length If the input reflection of a transmission line is known, then the line length can be determined by observing the periodicity of the reflection The peak of the input reflection can be used to determine line and load impedance values Differential Signaling 5 Two Port Network Theory Network theory is based on the property that a linear system can be completely characterized by parameters measured ONLY at the input & output ports without regard to the content of the system Networks can have any number of ports, however, consideration of a 2-port network is sufficient to explain the theory A 2-port network has 1 input and 1 output port. The ports can be characterized with many parameters, each parameter has a specific advantage Each Parameter set is related to 4 variables 2 independent variables for excitation 2 dependent variables for response Differential Signaling 6 Network characterized with Port Impedance Measuring the port impedance is network is the most simplistic and intuitive method of characterizing a network I1 Port 1 I2 V1 + - 2- port 2-port Networ Network k + V 2 - Port 2 Case 1: Inject current I1 into port 1 and measure the open circuit voltage at port 2 and calculate the resultant impedance from port 1 to port 2 Z 21 Vopen, port2 I port1 Case 2: Inject current I1 into port 1 and measure the voltage at port 1 and calculate the resultant input impedance Z11 Vopen, port1 I 1 Differentialport Signaling 7 Impedance Matrix 8 A set of linear equations can be written to describe the network in terms of its port impedances V1 Z11I1 Z12 I 2 V2 Z 21I1 Z 22 I 2 Or V1 Z11 Z12 I1 V2 Z 21 Z 22 I 2 Where: Vi Z ij Ij Open Circuit Voltage measured at Port i Current Injected at Port j Zii the impedance looking into port i Zij the impedance between port i and j If the impedance matrix is known, the response of the system can be predicted for any input Differential Signaling Impedance Matrix: Example #2 Calculate the impedance matrix for the following circuit: R2 R1 Port 1 R3 Differential Signaling Port 2 9 Impedance Matrix: Example #2 10 Step 1: Calculate the input impedance R2 R1 + I1 V1 V1 I1 ( R1 R3 ) V1 Z11 R1 R3 I1 R3 Step 2: Calculate the impedance across the network R1 R2 + I1 R3 V2 - R3 V2 V1 R1 R3 R3 I1 ( R3 R1 ) I1 R3 R1 R3 V2 Z R3 Differential Signaling 21 I1 Impedance Matrix: Example #2 Step 3: Calculate the Impedance matrix Assume: R1 = R2 = 30 ohms R3=150 ohms Z11 R1 R3 180 Z 21 30 180 30 Z Matrix 30 180 Differential Signaling 11 Measuring the impedance matrix Question: What obstacles are expected when measuring the impedance matrix of the following transmission line structure assuming that the micro-probes have the following parasitics? Lprobe=0.1nH Cprobe=0.3pF Assume F=5 GHz Port 1 T-line 0.1nH 0.3pF 0.1nH 0.3pF Zo=50 ohms, length=5 in Differential Signaling Port 2 12 Measuring the impedance matrix 13 Answer: Open circuit voltages are very hard to measure at high frequencies because they generally do not exist for small dimensions Open circuit capacitance = impedance at high frequencies Probe and via impedance not insignificant Without Probe Capacitance Port 1 0.1nH 0.3pF 0.1nH 0.1nH T-line T-line Zo = 50 Port 2 Port 0.3pF Port 1 Port 2 Z21 = 50 ohms Zo=50 ohms, length=5 in With Probe Capacitance @ 5 GHz Zo = 50 Z probe_ L 2fL 3 1 Z probe_ C 106 2fC Port 2 Port 1 106 ohms Differential Signaling 106 ohms Z21 = 63 ohms Advantages/Disadvantages of Impedance Matrix 14 Advantages: The impedance matrix is very intuitive Relates all ports to an impedance Easy to calculate Disadvantages: Requires open circuit voltage measurements Difficult to measure Open circuit reflections cause measurement noise Open circuit capacitance not trivial at high frequencies Note: The Admittance Matrix is very similar, however, it is characterized with short circuit currents instead of open circuit voltages Differential Signaling 15 Scattering Matrix (S-parameters) Measuring the “power” at each port across a well characterized impedance circumvents the problems measuring high frequency “opens” & “shorts” The scattering matrix, or (S-parameters), characterizes the network by observing transmitted & reflected power waves a2 a1 Port 1 2-port Network R R Port 2 b2 b1 ai represents the square root of the power wave injected into port i Vi V2 P P ai R R bj represents the power wave coming out of port j Differential Signaling bj Vj R Scattering Matrix 16 A set of linear equations can be written to describe the network in terms of injected and transmitted power waves b1 S11a1 S12a2 b2 S 21a1 S 22a2 b1 S11 S12 a1 b2 S 21 S 22 a2 Where: bi Sij aj Power measured at port i Power injected at port j Sii = the ratio of the reflected power to the injected power at port i Sij = the ratio of the power measured at port j to the power injected at port i Differential Signaling Making sense of S-Parameters – Return Loss When there is no reflection from the load, or the line length is zero, S11 = Reflection coefficient R=50 Zo Z=-l b1 S11 a1 a 20 R=Zo Z=0 V1 Vreflected Z o 50 V1 R o Vincident Z o 50 V1 V1 R S11 is measure of the power returned to the source, and is called the “Return Loss” Differential Signaling 17 Making sense of S-Parameters – Return Loss 18 When there is a reflection from the load, S11 will be composed of multiple reflections due to the standing waves 1 (l ) Z in Z (l ) Z o 1 (l ) Zo Z=-l RL Z=0 If the network is driven with a 50 ohm source, then S11 is calculated using the input impedance instead of Zo 50 ohms S 11 Z in 50 Z in Z in 50 S11 of a transmission line will exhibit periodic effects due to the standing waves Differential Signaling Example #3 – Interpreting the return loss Based on the S11 plot shown below, calculate both the impedance and dielectric constant R=50 Zo R=50 L=5 inches 0.45 S11, Magnitude 0.4 0.35 0.3 0.25 0.2 0.15 0.1 0.05 0 1.0 1.5 2.0 2.5 3..0 3.5 Differential Signaling Frequency, GHz 4.0 4.5 5.0 19 Example – Interpreting the return loss 0.45 1.76GHz 2.94GHz 0.4 S11, Magnitude 20 Peak=0.384 0.35 0.3 0.25 0.2 0.15 0.1 0.05 0 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 Frequency, GHz Step 1: Calculate the time delay Step 2: Calculate Er using the velocity of the t-line using the peaks 1 c 3 108 m / s v 1 f peaks 2.94GHz 1.76GHz TD Er Er 2TD 1 TD 423.7 ps TD / inch 84.7 ps / inch 39.37inch / m) TD / inch 423.7 ps / 5" 84.7 ps / inch Differential Signaling Er 1.0 Example – Interpreting the return loss Step 3: Calculate the input impedance to the transmission line based on the peak S11 at 1.76GHz S11 21 Z in 50 0.384 Z in 50 Z in 112.33 Note: The phase of the 50 Z o j 4fl LC reflection should be either ( x) o e 2l e 50 Z o +1 or -1 at 1.76 GHz because it is aligned with the e j 4 fl LC e j 4 1.76GHz( 5)84.7 ps e j 9.366 1 incident Step 4: Calculate the characteristic impedance based on the input impedance for x=-5 inches 50 Z o (1) 50 Z o 1 ( x 5) Z in Z o 112.33 Z o 50 Z o 1 ( x 5) 1 (1) 50 Z o 1 Z o 74.9 Er=1.0 and Zo=75 ohms Differential Signaling Making sense of S-Parameters – Insertion Loss When power is injected into Port 1 with source impedance Z0 and measured at Port 2 with measurement load impedance Z0, the power ratio reduces to a voltage ratio b2 S 21 a1 a 20 a1 V1 Zo V2 Z o V2 Vtransmitted Vincident V1 V1 a =0 Zo 2 2-port Network Zo V2 b2 b1 S21 is measure of the power transmitted from port 1 to port 2, and is called the “Insertion Loss” Differential Signaling 22 Loss free networks 23 For a loss free network, the total power exiting the N ports must equal the total incident power Pincident Pexit If there is no loss in the network, the total power leaving the network must be accounted for in the power reflected from the incident port and the power transmitted through network Preflected _ port1 Pincident Ptransmitted _ port1 port2 Pincident 1 Since s-parameters are the square root of power ratios, the following is true for loss-free networks S11 S21 2 2 1 If the above relationship does not equal 1, then there is loss in the network, and the difference is proportional to the power dissipated by the network Differential Signaling Insertion loss example 24 Question: What percentage of the total power is dissipated by the transmission line? Estimate the magnitude of Zo (bound it) S-parameters; 5 inch microstrip 1.2 1 Magnitude 0.8 S(1,1) S(1,2) 0.6 0.4 0.2 0 0.E+00 2.E+09 4.E+09 6.E+09 8.E+09 Frequency, Hz Differential Signaling 1.E+10 1.E+10 Insertion loss example 25 What percentage of the total power is dissipated by the transmission line ? What is the approximate Zo? How much amplitude degradation will this t-line contribute to a 8 GT/s signal? If the transmission line is placed in a 28 ohm system (such as Rambus), will the amplitude degradation estimated above remain constant? Estimate alpha for 8 GT/s signal S-parameters; 5 inch microstrip; 1.2 1 S(1,1) Magnitude 0.8 S(1,2) 0.6 0.4 0.2 0 0.E+00 2.E+09 4.E+09 6.E+09 Differential Signaling Frequency, Hz 8.E+09 1.E+10 Insertion loss example Answer: Since there are minimal reflections on this line, alpha can be estimated directly from the insertion loss S21~0.75 at 4 GHz (8 GT/s) When the reflections are minimal, alpha can be estimated S21 el 0.75 e (5) 0.057 If S11 < ~ 0.2 (-14 dB), then the above approximation is valid If the reflections are NOT small, alpha must be extracted with ABCD parameters (which are reviewed later) The loss parameter is “1/A” for ABCD parameters ABCE will be discussed later. Differential Signaling 26 Important concepts demonstrated The impedance can be determined by the magnitude of S11 The electrical delay can be determined by the phase, or periodicity of S11 The magnitude of the signal degradation can be determined by observing S21 The total power dissipated by the network can be determined by adding the square of the insertion and return losses Differential Signaling 27 A note about the term “Loss” 28 True losses come from physical energy losses Ohmic (I.e., skin effect) Field dampening effects (Loss Tangent) Radiation (EMI) Insertion and Return losses include effects such as impedance discontinuities and resonance effects, which are not true losses Loss free networks can still exhibit significant insertion and return losses due to impedance discontinuities Differential Signaling Advantages/Disadvantages of S-parameters Advantages: Ease of measurement Much easier to measure power at high frequencies than open/short current and voltage S-parameters can be used to extract the transmission line parameters n parameters and n Unknowns Disadvantages: Most digital circuit operate using voltage thresholds. This suggest that analysis should ultimately be related to the time domain. Many silicon loads are non-linear which make the job of converting s-parameters back into time domain non-trivial. Conversion between time and frequency domain introduces errors Differential Signaling 29 Cascading S parameter 30 3 cascaded s parameter blocks a11 a21 b12 b22 a13 s111 s121 s113 s123 s211 s221 b11 a13 s213 s223 s11 s12 s112 s122 b21 a12 s212 s222 a22 b13 s21 s22 b13 While it is possible to cascade s-parameters, it gets messy. Graphically we just flip every other matrix. Mathematically there is a better way… ABCD parameters We will analyzed this later with signal flow graphs Differential Signaling ABCD Parameters 31 The transmission matrix describes the network in terms of both voltage and current waves I1 V1 V1 AV2 BI 2 I2 2-port Network V2 The coefficients can be defined using superposition V1 A V2 I 2 0 V1 I1 B C I 2 V 0 V2 2 Differential Signaling I1 CV2 DI 2 V1 A B V2 I1 C D I 2 I 2 0 I1 D I2 V2 0 Transmission (ABCD) Matrix 32 Since the ABCD matrix represents the ports in terms of currents and voltages, it is well suited for cascading elements I3 I2 I1 A B C D1 V1 V2 A B C D2 V3 The matrices can be cascaded by multiplication V1 I1 V2 I2 V2 A B C D 1 I2 A V3 D 2 I3 C B V1 A B A B V3 I1 C D 1 C D 2 I 3 This is the best way to cascade elements in the frequency domain. Differential Signaling It is accurate, intuitive and simplistic. Relating the ABCD Matrix to Common Circuits Z Port 1 Y Port 1 Z1 Port 1 A 1 B Z C 0 D 1 Port 2 A 1 C Y Port 2 Z2 Z3 Port 2 Y3 Port 1 Y1 Port 1 Y2 Zo , l Port 2 Port 2 Assignment 6: Convert these to s-parameters B0 D 1 A 1 Z1 / Z 3 B Z1 Z 2 Z1Z 2 / Z 3 C 1 / Z3 D 1 Z 2 / Z3 A 1 Y2 / Y3 B 1 / Y3 C Y1 Y2 Y1Y2 / Y3 D 1 Y1 / Y3 A cosh( l ) B Z o sinh( l ) C (1 / Z o ) sinh( l ) D cosh( l ) Differential Signaling 33 Converting to and from the S-Matrix The S-parameters can be measured with a VNA, and converted back and forth into ABCD the Matrix Allows conversion into a more intuitive matrix Allows conversion to ABCD for cascading ABCD matrix can be directly related to several useful circuit topologies (1 S11 )(1 S 22 ) S12 S 21 A 2 S 21 S11 A B / Z o CZ o D A B / Z o CZ o D (1 S11 )(1 S 22 ) S12 S 21 B Zo 2 S 21 2( AD BC ) S12 A B / Z o CZ o D 1 (1 S11 )(1 S 22 ) S12 S 21 C 2S 21 Zo 2 S 21 A B / Z o CZ o D (1 S11 )(1 S 22 ) S12 S 21 D 2S 21 S11 Differential Signaling A B / Z o CZ o D A B / Z o CZ o D 34 ABCD Matrix – Example #1 35 Create a model of a via from the measured s-parameters Port 1 Port 2 S11 S12 0.110 j 0.153 0.798 j 0.572 S 21 S 22 0.798 j 0.572 0.110 j 0.153 Differential Signaling ABCD Matrix – Example #1 36 The model can be extracted as either a Pi or a T network L1 L2 Port 1 CVIA Port 2 The inductance values will include the L of the trace and the via barrel (it is assumed that the test setup minimizes the trace length, and subsequently the trace capacitance is minimal The capacitance represents the via pads Differential Signaling ABCD Matrix – Example #1 Assume the following s-matrix measured at 5 GHz S11 S12 0.110 j 0.153 0.798 j 0.572 S 21 S 22 0.798 j 0.572 0.110 j 0.153 Differential Signaling 37 ABCD Matrix – Example #1 Assume the following s-matrix measured at 5 GHz S11 S12 0.110 j 0.153 0.798 j 0.572 S 21 S 22 0.798 j 0.572 0.110 j 0.153 Convert to ABCD parameters A B 0.827 C D j 0.0157 j 20.08 0.827 Differential Signaling 38 ABCD Matrix – Example #1 39 Assume the following s-matrix measured at 5 GHz S11 S12 0.110 j 0.153 0.798 j 0.572 S 21 S 22 0.798 j 0.572 0.110 j 0.153 Convert to ABCD parameters A B 0.827 C D j 0.0157 j 20.08 0.827 Relating the ABCD parameters to the T circuit topology, the capacitance and inductance is extracted from C & A Z1 Port 1 Z2 Z3 C j 0.0157 Port 2 1 Z3 1 CVIA 0.5 pF 1 j 2fCVIA Z1 j 2fL 0.827 1 L1 L2 0.35nH Z3 1 /( j 2fCVIA ) Differential Signaling A 1 ABCD Matrix – Example #2 40 Calculate the resulting s-parameter matrix if the two circuits shown below are cascaded Port 1 Port 2 2-port Network X Network 50 Port 1 50 Port 2 2-port Network Y Network 50 50 Port 1 50 S X 11 S X 12 SX S X 21 S X 22 SY 11 SY 12 SY SY 21 SY 22 2-port Network Y Network 2-port Network X Network S XY ? Differential Signaling 50 Port 2 ABCD Matrix – Example #2 41 Step 1: Convert each measured S-Matrix to ABCD Parameters using the conversions presented earlier AX S X TX CX BX DX AY SY TY CY BY DY Step 2: Multiply the converted T-matrices TXY AX TX TY CX BX AY DX CY BY AXY DY C XY BXY DXY Step 3: Convert the resulting Matrix back into Sparameters using thee conversions presented earlier TXY S XY S X 11 S X 12 S X 21 S X 22 Differential Signaling Advantages/Disadvantages of ABCD Matrix Advantages: The ABCD matrix is very intuitive Describes all ports with voltages and currents Allows easy cascading of networks Easy conversion to and from S-parameters Easy to relate to common circuit topologies Disadvantages: Difficult to directly measure Must convert from measured scattering matrix Differential Signaling 42 Signal flow graphs – Start with 2 port first The wave functions (a,b) used to define s-parameters for a two-port network are shown below. The incident waves is a1, a2 on port 1 and port 2 respectively. The reflected waves b1 and b2 are on port 1 and port 2. We will use a’s and b’s in the s-parameter follow slides Differential Signaling 43 Signal Flow Graphs of S Parameters “In a signal flow graph, each port is represented by two nodes. Node an represents the wave coming into the device from another device at port n, and node bn represents the wave leaving the device at port n. The complex scattering coefficients are then represented as multipliers (gains) on branches connecting the nodes within the network and in adjacent networks.”* Example a1 s21 b2 S s22 s11 L s12 b1 a2 s11 a1 S L 0 b1 a2 0 Measurement equipment strives to be match i.e. reflection coefficient is 0 See: http://cp.literature.agilent.com/litweb/pdf/5952-1087.pdf Differential Signaling 44 Mason’s Rule ~ Non-Touching Loop Rule T (1 (1) T (1 (1) mk k k L(mk ) (k ) 45 ) mk mk L(mk )) mk T is the transfer function (often called gain) Tk is the transfer function of the kth forward path L(mk) is the product of non touching loop gains on path k taken mk at time. L(mk)|(k) is the product of non touching loop gains on path k taken mk at a time but not touching path k. mk=1 means all individual loops Differential Signaling Voltage Transfer function 46 What is really of most relevance to time domain analysis is the voltage transfer function. It includes the effect of non-perfect loads. We will show how the voltage transfer functions for a 2 port network is given by the following equation. s21 2 L 1 1 s 1 s11 s s22 L s21 s12 L s s11 s22 L s Notice it is not S21 Differential Signaling Forward Wave Path 47 Z0 Vs ( ZS Z0) S a1 s21 b2 s22 s11 L s12 b1 b2 Vs s21 a2 Z0 ( ZS Z0) 1 s11 s s22 L s21 s12 L s s11 s22 L s Differential Signaling Reflected Wave Path 48 Z0 Vs ( ZS Z0) S a1 s21 b2 s22 s11 L s12 b1 a2 Vs s21 L a2 Z0 ( ZS Z0) 1 s11 s s22 L s21 s12 L s s11 s22 L s Differential Signaling Combine b2 and a2 s21 b2 Vs 49 ( ZS Z0) 1 s11 s s22 L s21 s12 L s s11 s22 L s Vs b2 Z0 a2 Vs s21 1 L Z0 ( ZS Z0) 1 s11 s s22 L s21 s12 L s s11 s22 L s Differential Signaling Convert Wave to Voltage - Multiply by sqrt(Z0) s Vo Vs s21 1 L Vo Vs 50 Z0 ( ZS Z0) 1 s11 s s22 L s21 s12 L s s11 s22 L s ZS Z0 ZS Z0 1 s 1 ZS Z0 ZS Z0 s21 1 L 1 s 2 Z0 ( ZS Z0) 1 s 2 1 s11 s s22 L s21 s12 L s s11 s22 L s Differential Signaling Voltage transfer function using ABCD Let’s see if we can get this results another way ( 1 s11) ( 1 s22) s12 s21 [ ( 1 s11) ( 1 s22) s12 s21] Z0 2 s21 2 s21 ABCD_CHANNEL ( 1 s11) ( 1 s22) s12 s21 ( 1 s11) ( 1 s22) s12 s21 2 s21 Z0 2 s21 ABCD_SOURCE ZL Z0 1 L 1 L 1 Zs 0 1 1 0 ABCD_LOAD 1 1 ZL Zs Z0 1 s 1 s Differential Signaling 51 Cascade [ABCD] to determine system [ABCD] VOLTAGE_TRANSFER_FUNCTION 1 s 1 Z0 1 s 1 0 52 ABCD_SOURCE ABCD_CHANNEL ABCD_LOAD 1 0 ( 1 s11) ( 1 s22) s12 s21 [ ( 1 s11) ( 1 s22) s12 s21] Z0 2 s21 2 s21 1 1 ( 1 s11) ( 1 s22) s12 s21 ( 1 s11) ( 1 s22) s12 s21 Z0 1 L 2 s21 Z0 2 s21 1 L Simplify 1 s22 s11 s s11 s22 s s12 s21 s 1 s11 s s22 L s11 s22 s L s12 s21 s L 2 Z0 1 s s21 1 L 1 s s21 1 s22 L s11 s11 s22 L s12 s21 L 1 1 s22 s11 s11 s22 s12 s21 2 s21 s21 Z0 1 L Differential Signaling Extract the voltage transfer function "A" parameter which input over output transfer. We are looking for "1/A" which is output over input 1 s11 s s22 L s11 s22 s L s12 s21 s L 2 1 s s21 1 L 1 Simplify and re-arange s21 1 L 1 s 2 1 s11 s s22 L s12 s21 s L s11 s22 s L Same as with flow graph analysis Differential Signaling 53 Cascading S-Parameter 54 As promised we will now look at how to cascade sparameters and solve with Mason’s rule The problem we will use is what was presented earlier The assertion is that the loss of cascade channel can be determine just by adding up the losses in dB. We will show how we can gain insight about this assertion from the equation and graphic form of a solution. a11 a21 b12 b22 a13 s111 s121 s113 s123 s211 s221 s213 s223 s112 s122 b11 a13 b21 a12 s212 s222 a22 b13 Differential Signaling s11 s12 s21 s22 b13 Creating the signal flow graph a11 a21 b12 b22 a13 s113 s123 s211 s221 s213 s223 b11 s212 s222 b21 a12 s211 B21 1 s221 B11 a13 s111 s121 s112 s122 A11 55 s121 A21 A12 s212 a22 b13 B22 1 s11 s12 s21 s22 s213 A13 s112 s222 1 B12 s122 A22 B23 s113 1 s223 s123 B13 We map output a to input b and visa versa. Next we define all the loops Loop “A” and “B” do not touch each other Differential Signaling b13 A23 Use Mason’s rule A11 s211 B21 1 56 A12 s221 B11 b6 a1 s121 s212 s213 1 B22 A13 s112 s222 A21 1 B12 s122 s113 B13 s21 s21 s21 2 1 3 2 3 1 3 2 s221s112s222s113 2 There is only one forward path a11 to b23. There are 2 non touching looks Differential Signaling A23 Mason’s Rule 1 s22 s11 s22 s11 s11 s22 s12 s21 2 s223 s123 1 A22 1 B23 Evaluate the nature of the transfer function 57 Assumption is that these are ~ 0 b6 a1 s21 s21 s21 1 2 3 1 s22 s11 s22 s11 s11 s22 s12 s21 s22 s11 s22 s11 2 1 3 2 3 1 2 2 2 1 • If response is relatively flat and reflection is relatively low – Response through a channel is s211*s212*213… Differential Signaling 3 4 Jitter and dB Budgeting S211 e j 211 S21 e j 211 2 S21 S21 1 Smag e S Change s21 into a phasor 58 2 j j 213 S213 e j 211 21 =2 213 s21 e 3 Insertion loss in db 20 log S21 S21 1 2 20 log s21 s21 3 = 20logs212 20logs213 1 i.e. For a budget just add up the db’s and jitter db sys dbi i1 delay n i i1 n Differential Signaling Differential S-Parameters 59 Differential S-Parameters are derived from a 4-port measurement a2 a1 b1 4-port b2 b1 S11 S12 S13 S14 b2 S21 S22 S23 S24 S31 S32 S33 S34 S41 S42 S43 S44 a3 a4 b3 b3 b4 b4 = a1 a2 a3 a4 Traditional 4-port measurements are taken by driving each port, and recording the response at all other ports while terminated in 50 ohms Although, it is perfectly adequate to describe a differential pair with 4-port single ended s-parameters, it is more useful to convert to a multi-mode port Differential Signaling 60 Differential S-Parameters It is useful to specify the differential S-parameters in terms of differential and common mode responses Differential stimulus, differential response Common mode stimulus, Common mode response Differential stimulus, common mode response (aka ACCM Noise) Common mode stimulus, differential response This can be done either by driving the network with differential and common mode stimulus, or by converting the traditional 4-port s-matrix adm2 bdm1 acm1 bcm1 Multi-Mode Port bdm2 acm2 Multi-Mode Port 2 Multi-Mode Port 1 adm1 bdm1 DS11 DS12 DCS11 DCS12 adm1 bdm2 DS21 DS 22 DCS21 DCS22 adm2 CDS11 CDS12 CS11 CS12 acm1 CS21 CS 22 acm2 bcm1 bcm2 = CDS21 CDS 22 bcm2 Matrix assumes differential and common mode stimulus Differential Signaling Explanation of the Multi-Mode Port Differential Matrix: Differential Stimulus, differential response i.e., DS21 = differential signal [(D+)-(D-)] inserted at port 1 and diff signal measured at port 2 Common mode conversion Matrix: Differential Stimulus, Common mode response. i.e., DCS21 = differential signal [(D+)-(D-)] inserted at port 1 and common mode signal [(D+)+(D-)] measured at port 2 bdm1 DS11 DS12 DCS11 DCS12 adm1 bdm2 DS21 DS 22 DCS21 DCS22 adm2 CDS11 CDS12 CS11 CS12 acm1 CS21 CS 22 acm2 bcm1 bcm2 = CDS21 CDS 22 61 differential mode conversion Matrix: Common mode Matrix: Common mode Stimulus, differential Common mode stimulus, common mode mode response. i.e., DCS21 = common Response. i.e., CS21 = Com. mode signal mode signal [(D+)+(D-)] inserted at port [(D+)+(D-)] inserted at port 1 and Com. mode 1 and differential mode signal [(D+)-(D-)] Differential Signaling signal measured at port 2 measured at port 2 Differential S-Parameters 62 Converting the S-parameters into the multi-mode requires just a little algebra Example Calculation, Differential Return Loss The stimulus is equal, but opposite, therefore: a3 a1 ; a4 a2 b DS11 dm1 adm1 adm2 0;acm 0 b b 1 3 a1 a3 1 a2 a4 0 b1 S11a1 S12a2 S13a3 S14a4 4-port 2-port Network 3 2 4 b3 S31a1 S32a2 S33a3 S34a4 b1 b3 a1 ( S11 S31 ) a2 ( S12 S32 ) a3 ( S13 S33 ) a4 ( S14 S34 ) Assume a symmetrical network and substitute DS11 a3 a1 ; a4 a2 S12 S34 ; S32 S14 1 S11 S31 S13 S33 2 Other conversions that are useful for a differential bus are shown Differential Insertion Loss: DS 21 1 S 21 S 41 S 23 S 43 2 Differential to Common Mode Conversion (ACCM): CDS 21 1 S21 S43 S23 S41 2 Similar techniquesDifferential can be used for all multi-mode Parameters Signaling Next class we will develop more differential concepts Differential Signaling 63 backup review 64 Differential Signaling Advantages/Disadvantages of Multi-Mode Matrix over Traditional 4-port Advantages: Describes 4-port network in terms of 4 two port matrices Differential Common mode Differential to common mode Common mode to differential Easier to relate to system specifications ACCM noise, differential impedance Disadvantages: Must convert from measured 4-port scattering matrix Differential Signaling 65 High Frequency Electromagnetic Waves In order to understand the frequency domain analysis, it is necessary to explore how high frequency sinusoid signals behave on transmission lines The equations that govern signals propagating on a transmission line can be derived from Amperes and Faradays laws assumimng a uniform plane wave The fields are constrained so that there is no variation in the X and Y axis and the propagation is in the Z direction This assumption holds true for transmission lines as long as the wavelength of the signal is much greater than the trace width X Direction of propagation Z m in 3 108 39.4 s m1 W f r For typical PCBs at 10 GHz with 5 mil traces (W=0.005”) Y 0.59" 0.005" Differential Signaling 66 High Frequency Electromagnetic Waves For sinusoidal time varying uniform plane waves, Amperes and Faradays laws reduce to: Amperes Law: A magnetic Field will be induced by an electric current or a time varying electric field By z Faradays Law: An electric field will be generated by a time varying magnetic flux jE x E x j B y z Note that the electric (Ex) field and the magnetic (By) are orthogonal Differential Signaling 67 High Frequency Electromagnetic Waves If Amperes and Faradays laws are differentiated with respect to z and the equations are written in terms of the E field, the transmission line wave equation is derived B y B y 2 Ex 2 Ex 1 j 2 jE x 2 z z z z j 2 Ex 2 2 j E x 0 2 z This differential equation is easily solvable for Ex: Ex ( z ) C1e j ( ) z C2e Differential Signaling j ( ) z 68 High Frequency Electromagnetic Waves 69 The equation describes the sinusoidal E field for a plane wave in free space Note the positive exponent j ( ) z M Ex ( z ) E e Portion of wave traveling In the +z direction j ( ) z M E e is because the wave is traveling in the opposite direction Portion of wave traveling In the -z direction = permittivity in Farads/meter (8.85 pF/m for free space) (determines the speed of light in a material) permeability in Henries/meter (1.256 uH/m for free space = and non-magnetic materials) Since inductance is proportional to & capacitance is proportional to , then is analogous to LC in a transmission line, which is the propagation delay Differential Signaling High Frequency Voltage and Current Waves 70 The same equation applies to voltage and current waves on a transmission line Incident sinusoid Reflected sinusoid z=-l RL z=0 If a sinusoid is injected onto a transmission line, the resulting voltage is a function of time and distance from the load (z). It is the sum of the incident and reflected values z V ( z, t ) Vine e Voltage wave traveling towards the load jt z Vref e e jt j t Note: is added to specifically represent the time varying Sinusoid, which was implied in the previous derivation Voltage wave reflecting off the Load and traveling towards the source Differential Signaling e High Frequency Voltage and Current Waves 71 The parameters in this equation completely describe the voltage on a typical transmission line z V ( z, t ) Vine e j j LC jt z Vref e e jt = Complex propagation constant – includes all the transmission line parameters (R, L C and G) (For the loss free case) ( R jL)(G jC ) (lossy case) = Attenuation Constant (attenuation of the signal due to transmission line losses) 1 C L (For good conductors) R G 2 L C = Phase Constant (related to the propagation delay across the transmission line) LC (For good conductors and good dielectrics) Differential Signaling High Frequency Voltage and Current Waves The voltage wave equation can be put into more intuitive terms by applying the following identity: j e cos( ) j sin( ) V ( z , t ) Vine ( j ) z e jt Vref e ( j ) z e jt Subsequently: z z e Vin cos (t ) j sin (t ) z z ezVref cos (t ) j sin (t ) z The amplitude is degraded by z e The waveform is dependent on the driving function (cos t j sin t ) & the delay of the line LC Differential Signaling 72 Interaction: transmission line and a load 73 The reflection coefficient is now a function of the Zo discontinuities AND line length Influenced by constructive & destructive combinations of the forward & reverse waveforms Zo (l ) Zl (Assume a line length of l (z=-l)) Z=-l Z=0 V (l ) Vinel Vref el Vin el oel Vinel 1 (l ) (l ) Vref el Vine l o e 2l Z l Z o 2l e Zl Zo This is the reflection coefficient looking into a t-line of length l Differential Signaling Interaction: transmission line and a load 74 If the reflection coefficient is a function of line length, then the input impedance must also be a function of length Zin RL Z=-l Z=0 V (l ) Vine l Vref el Vin e l o el Vine l 1 (l ) 1 1 l l I (l ) Vine Vref e Vine l 1 (l ) Zo Zo Vine l 1 (l ) V (l ) 1 (l ) Z in Z (l ) Zo 1 I (l ) 1 (l ) Vine l 1 (l ) Zo Note: (l ) is dependent on and l This is the input impedance looking into a t-line of length l Differential Signaling Line & load interactions In chapter 2, you learned how to calculate waveforms in a multi-reflective system using lattice diagrams Period of transmission line “ringing” proportional to the line delay Remember, the line delay is proportional to the phase constant In frequency domain analysis, the same principles apply, however, it is more useful to calculate the frequency when the reflection coefficient is either maximum or minimum This will become more evident as the class progresses To demonstrate, lets assume a loss free transmission line j R jL G jC 0 R G 0 j j 2 2 LC j LC Differential Signaling 75 Line & load interactions 76 Remember, the input reflection takes the form (l ) o e 2l The frequency where the values of the real & imaginary reflections are zero can be calculated based on the line length o e 2 ( l ) o e j 2 ( l ) o e j 2l 4fl LC n 2 LC Term 1 Term 2 o cos 4fl LC j sin 4fl LC 4fl LC n n Term 1=0 n Term 2=0 f Term 2 = f Term 1 = 4l LC o o 8l LC n 1,2,3... n 1,3,5... Note that when the imaginary portion is zero, it means the phase of the incident & reflected waveforms at the input are aligned. Also notice that value of “8” and “4” in the terms. Differential Signaling Example #1: Periodic Reflections Calculate: 1. Line length 2. RL (l ) (assume a very low loss line) 77 Er_eff=1.0 Zo=75 Z=-l Z=0 2.5E-01 Imaginary 2.0E-01 Real Reflection Coeff. 1.5E-01 1.0E-01 5.0E-02 0.0E+00 -5.0E-02 -1.0E-01 -1.5E-01 -2.0E-01 -2.5E-01 0.0E+00 5.0E+08 1.0E+09 1.5E+09 Frequency RL 2.0E+09 Differential Signaling 2.5E+09 3.0E+09 Example #1: Solution Step 1: Determine the periodicity zero crossings or peaks & use the relationships on page 15 to calculate the electrical length 3 1 1 f n 3 f n 1 1.76GHz 588MHz 1.176GHz 4l LC 4l LC 2l LC 1 1 TD l LC 425 ps 2( f n 3 f n 1 ) 2.35GHz Imaginary Differential Signaling 78 Example #1: Solution (cont.) 79 Note the relationship between the peaks and the electrical length 1 TD l LC 2( f n 3 f n 1 ) This leads to a very useful equation for transmission lines Fpeaks 1 2TD Since TD and the effective Er is known, the line length can be calculated as in chapter 2 length TD 425 ps 0.127m 5in Er _ eff 1 s 8 3 10Signaling m c Differential Example #1: Solution (cont.) The load impedance can be calculated by observing the peak values of the reflection When the imaginary term is zero, the real term will peak, and the maximum reflection will occur If the imaginary term is zero, the reflected wave is aligned with the incident wave and the phase term = 1 RL Z o 2l RL 75 (l ) e (1) 0.2 RL Z o RL 75 RL 50 Important Concepts demonstrated The impedance can be determined by the magnitude of the reflection The line length can be determined by the phase, or periodicity of the reflection Differential Signaling 80