Download electro_magnetic_induction

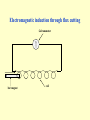
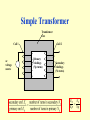
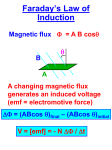
Electromagnetic Induction
Electromagnetic induction through flux cutting
Galvanometer
N
S
bar magnet
coil
Requirements for Induced EMF
For an emf to be induced in a conductor there must be a changing magnetic field;
that is, relative motion between the conductor and the magnetic flux. In other
words, the conductor must cut the magnetic flux or the magnetic flux must cut the
conductor.
In addition, it can be demonstrated that a larger emf is produced if:
– the magnet or coil is moved faster
– the number of windings of the coil is increased
– a stronger magnet is used
In other words, the induced emf depends on the strength of the magnetic
field, the rate at which the flux cuts (or is cut by) the conductor and the
number of turns in the coil.
The direction of the induced emf (direction of current flow) depends on
the polarity of the magnet and its direction of movement relative to the
coil.
Electromagnetic induction through flux linkage
Coil 1
Coil 2
ferromagnetic
material
It may be observed that a momentary
deflection of the galvanometer occurs
when the current in coil 1 is switched on.
A momentary deflection in the opposite
direction is observed when the current is
switched off.
No deflection is observed when the
current in coil 1 is steady.
From these observations, we may
conclude that an emf is induced in coil 2
due to a changing current in coil 1.
Faraday’s Law of Electromagnetic Induction
•
Faraday’s law states that the emf, e, induced in a circuit is
proportional to the rate of change of flux linkage, where flux linkage
is the product of the magnetic flux through the circuit and the
number of turns N affected by the flux.
•
Mathematically, we may say that:
e  d/dt(N)
or
e  N.d/dt,
•
since N is normally constant.
If the flux, , is measured in webers and t is measured in seconds,
then Faraday’s law may be summarised as:
eN
d
dt
Lenz’s Law of Electromagnetic Induction
•
Faraday’s law gives the magnitude of the induced emf only. Its
direction is given by Lenz’s law, which states that the direction of the
induced emf is such that it opposes the cause which produces it.
•
For example, an increasing flux through a closed circuit will induce an
emf (and hence a current in the circuit) that generates a magnetic field
which tries to stop the increase in flux; that is, it opposes the applied
field (cause) that produces the emf.
•
Conversely, a decreasing flux will induce an emf and hence a current
that tries to increase the applied field, and stop it decreasing.
•
Lenz’s law can be combined with Faraday’s law into a single equation
that gives both the magnitude and direction of induced emf:
e  N
d
dt
Example
Calculate the average emf induced in a coil of 500 turns when the flux
linking it changes from 0.5mWb to 1mWb in 1 millisecond.
Solution
If the flux change is non-uniform and changes from an initial valuei to a
final value (f in a time of t, to average rate of change of flux is
(f - i )/t
Thus the average induced emf is given by the expression:
e = -N(f - i)/t
e = -N(f - i)/t volts
where: N = 500 turns
f = 10-3 Wb
i = 0.5 × 10-3 Wb
t = 0.001 s
e = -500(1 × 10-3 - 0.5 × 10-3)/10-3
= -250V
Simple Transformer
Transformer
core
Coil 1
ac
voltage
source
~
Coil 2
Primary
windings
(Np turns)
Secondary
windings
(Ns turns)
Es
N
 s
Ep N p
Ideal Transformer
primary input power = secondary output power
•
If we assume that the transformer is 100% efficient, i.e. there is no power
loss, then the input (primary) electrical power must equal the output
(secondary) power.
•
A transformer will never be 100% efficient as there will be power loss due
to, e.g. heat generation due to the resistance of the windings and hysteresis
effects.
•
For an ideal transformer we can say that
power in primary = power in secondary
or
Ep  Ip = Es × Is
where Ip and Is are the primary and secondary currents respectively.
Therefore
Ep
Np
Is


Ip
Es
Ns
An alternating source of emf with peak value 200V is applied to the primary
winding of a transformer. If the number of turns in the primary and
secondary windings are 500 and 25 respectively, calculate the peak value of
the voltage induced in the secondary winding. What is the value of the
secondary current if the primary current is 5mA?
Let Ep = peak value of voltage applied to primary
Es = peak value of voltage applied to secondary
Np = number of turns on primary
Ns = number of turns on secondary
Es/Ep = Ns/Np
Es = Ns/Np × Ep
Therefore: Es= (25/500) × 200 = 10V
Is = Np/Ns × Ip = (500/25) × 5mA = 0.1A.