Download Document

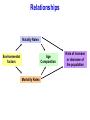
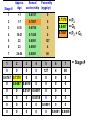
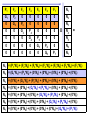
Population
Dynamics
Population – a group of organisms of the same
species occupying a particular space at a
particular time.
Demes – groups of interbreeding organisms
• local population
• smallest collective unit of a plant or animal
population
Populations are units of study.
Population Attributes
• Density – number of organisms per unit
area or per unit volume
• Affected by:
– Natality – the reproductive output (birth rate) of
a population
– Mortality – the death rate of organisms in a
population
– Immigration – number of organisms moving
into the area occupied by the population
– Emigration – number of organisms moving out
of the area occupied by the population
Population Density
Four primary population parameters:
Unitary and Modular Organisms
• Unitary organisms – individual units such
as humans or mice
• Modular organisms – organisms that do
not come in simple units of individuals
– Several grasses that are attached by runners
Density Examples
Two fundamental attributes that affect our choice of
techniques for population estimation are the size and
mobility of the organism with respect to humans.
Abundance and Animal Size
Birds are less abundant than mammals of equivalent size.
Density Relationships
Two Types of Density Estimates
• Absolute Density – a known density such
as #/m2
• Relative Density – we know when one area
has more individuals than another
Measuring Absolute Density
• Total Count – count the number of
organisms living in an area
– Human census, number of oak trees in a
wooded lot, number of singing birds in an area
– Total counts generally are not used very often
• Sampling Methods – use a sample to
estimate population size
– Either use the quadrat or capture-recapture
method
Quadrat Method
• A Quadrat is a sampling area of any shape
randomly deployed. Each individual
within the quadrat is counted and those
numbers are used to extrapolate
population size.
– Example: a 100 square centimeter metal
rectangle is randomly thrown four times and
all of the beetles of a particular species within
the square are counted each time: 19, 21, 17,
and 19. This translates to 19 beetles per 100
cm2 or 1900 per m2.
Transects as Quadrats
• Each transect was 110 meters long and 2m
wide (220 m2 or 0.022/ha). All trees taller
than 25 cm counted.
Capture-recapture Method
• Important tool for estimating density, birth
rate, and death rate for mobile animals.
• Method:
– Collect a sample of individuals, mark them,
and then release them
– After a period, collect more individuals from
the wild and count the number that have marks
– We assume that a sample, if random, will
contain the same proportion of marked
individuals as the population does
– Estimate population density
Peterson Method
Marked animals in
second sample
Total caught in
second sample
5 = 16
20 N
=
Marked animals in
first sample
Total population
size
N = 64
Assumptions For All CaptureRecapture Studies
• Marked and unmarked animals are
captured randomly.
• Marked animals are subject to the same
mortality rates as unmarked animals. The
Peterson method assumes no mortality
during the sampling period.
• Marked animals are neither lost or
overlooked.
Indices of Relative Density
• Assume that samples represent some
relatively constant but unknown
relationship to total population size.
– # cars in the Piggly Wiggly parking lot
• Provides an index of abundance
– Is population increasing, decreasing, or
staying the same
– Are there more animals in one location than
another?
– Can not quantify differences between sites
 Twice the number of tracks does not = twice
as many animals
Some Indices Used
• Traps
• Number of Fecal
Pellets
• Vocalization
Frequency
• Pelt Records
• Catch per Unit Fishing
Effort
•
•
•
•
•
Number of Artifacts
Questionnaires
Cover
Feeding Capacity
Roadside Counts
Natality
• Fecundity – physiological notion that
refers to an organism’s potential
reproductive potential
– Usually inversely proportional to the amount of
parental care given to young
• Fertility – Ecological concept that is based
on the number of viable offspring
produced during a specific period
– Realized fertility – actual fertility rate
 One birth per 15 years per human female in
the child-bearing ages
– Potential fertility – potential fertility rate
 One birth per 10 to 11 months per human
female in the child-bearing ages
Mortality
• Opposite of mortality is survival
• Longevity focuses on the age of death of
individuals in a population
– Potential longevity – maximum lifespan by an
individual of a particular species
 Set by the organisms physiology (dies of old age)
 Sometimes described as the average longevity of
individuals living in optimal conditions
– Realized longevity – actual life span of an organism
 Measured as an average for all animals living
under real environmental conditions
Determining Mortality
• Mark several individuals and measure how many survive
from time t to t+1.
• If abundance of successive age groups is known, then
you can estimate mortality between successive age
groups.
• Can use catch curves for fish:
Survival between
age 2 and 3=
147/292=0.50
Or develop regression
equation
292
147
Immigration and Emigration
• Seldom measured
• Assumed to be equal or insignificant
(island pop’s)
• However, dispersal may be a critical
parameter in population changes
Limitations of the Population Approach
• How to determine what exactly is a
population
– How clear are the boundaries?
• Population does not exist as an isolate
– Individuals interact with other members of the
community
Life Tables - Mortality
• Mortality is one of the four key parameters that
drive population changes.
• We can use a life table to answer particular
questions about population mortality rates.
– What life stage has the highest mortality?
– Do older organisms die more frequently than
young organisms
• A cohort life table is an age-specific summary of
the mortality rates operating on a cohort of
individuals.
• Cohort – a collective group of individuals
– Fish year class, all mice born in March, tadpoles from a
single frog, freshman year class
Cohort Life Table:
X = age
nx = number alive at time t
lx = proportion of organisms surviving from the start of the life
table to age x (ex: l1 = n1/n0, 0.217 = 25/115; l2=n2/n0,
0.165=19/115)
dx = number dying during the age interval x to x + 1 (ex:d0=n0-n1,
90 = 115-25; d1=n1-n2, 6=25-19)
qx = per capita rate of mortality during the age interval x to x + 1
(ex: q0=d0/n0, 0.78 =90/115; q1=d1/n1)
Formula’s For Cohort Life Table
• X = age group we decide on
• nx = observed
• lx = lx+1 = nx+1/nx (overall survival)
• dx = nx - nx+1 (age specific number dying)
• qx = dx / nx (age specific mortality rate)
Per Capita Rates
• Per capita is a presentation of data as a
proportion of the population.
• Suppose a disease kills 400 ducks:
– If total duck population = 250,000 then the per
capita mortality = 400/250,000 = 0.16%.
– If total duck population = 2,500 then the per
capita mortality = 400/2,500 = 16%.
• Per capita gives us an idea of how the
entire population is affected.
Survivorship Curve
A plot of nx on a Log scale from a starting
cohort of 1,000 individuals.
Three Types of General Curves
 Survival curve
Examples of Each Type:
•Type 1 – Humans
•Type 2 – Birds
•Type 3 - Fish
These curves are
models. Most real
curves are intermediate.
Mortality curve 
Static Life Table
Calculated by taking a cross section of a population at a
specific time:
Per Capita
Cohort Versus Static Life Tables
• Cohort follows an individual cohort
through time and static looks at all of the
individuals currently present.
• The two are equal if and only if the
environment does not change from year to
year and the population is at equilibrium.
– The human cohort life table for 1900 does little
good for predicting life expectancy for today.
How to Collect Life Table Data
1) Survivorship directly observed.
•
•
Follow an individual cohort through time at
close intervals.
Best to have since it generates a cohort life
table directly and does not assume that the
population is stable over time.
Balanus can affect
the survival of
Chthamalus as
determined by
survivorship curve
How to Collect Life Table Data
2) Age at Death Observed.
•
By determining how old individuals were
when they died, we can create a life table.
Based on 584
individuals plus
observed estimated
mortality for age 1 and
2 individuals
How to Collect Life Table Data
3) Age Structure Directly Observed.
•
We can construct a life table based on the
age structure of a population
–
•
Counting rings on a tree or a fish otolith.
Assume a constant age structure, which is
hardly the case.
Aging
• Does mortality increase with age
(senescence)?
This data proves
our simple theory of
senescence is not
correct
Mortality Rate (qx)
– Not for some Mediterranean fruit flies:
Intrinsic Capacity For Increase In Numbers
• By combining reproduction and mortality
estimates, we can determine net
population change (intrinsic capacity for
increase).
• The environment can influence population
mean longevity or survival rate, natality
rate, and growth rate.
– Can be summed with natality and death rate
Fertility Schedule
Population net reproductive rate
bx = natality
0.6% increase each generation
(lx)(bx) = reproductive output for that age class
R0 < 1 population is declining, R0 = 1 population is
stable, R0 > population is increasing.
Population Increase
• If survival and fertility rates do not
change, and no limit is placed on
population growth – at what rate will a
population increase?
• It seems we need to know age-specific
survival rates, age-specific fertility rates,
and age structure
– If all females in U.S. were >50 years old, no
new young would be produced.
• However, the age structure does not need
to be known!
Stable Age Distribution
• Given constant schedule of natality and
mortality rates, a population will
eventually reach a stable age distribution,
and will remain at this age distribution
indefinitely.
• Stable age distribution:
–
–
–
–
60% age 0
25% age 1
10% age 2
4% age 3
• Although the absolute number will
change, the proportion of each age class
remains constant!
For Example
This animal lives three
years, produces two young
at exactly one year, and
one young at exactly year
two, and no young year
three, then dies at end of
year 3.
If a population starts
with one individual at
age 0, the age
distribution quickly
becomes stable: 60%
age 0, 25% age 1,
10% age 2, and 4%
age 3.
Stable Age Distribution
When a population has reached the stable age
distribution, it will increase in numbers according to:
dN = rN Written in integral form  Nt = N0ert
dt
Nt = number of individuals at time t
N0 = number of individuals at time 0
e = 2.71828 (a constant)
r = intrinsic capacity for increase for the
particular environmental conditions
t = time
This equation describes the curve of geometric
increase in an expanding population (or geometric
decrease to zero if r is negative).
For Example:
N0ert = Nt
Any population on a
fixed age schedule of
natality and mortality
will change
geometrically.
This geometric change
will dictate a fixed and
unchanging age
distribution – the stable
age distribution.
Generation Time
• Generation time – mean period elapsing
between the production or ‘birth’ of
parents and the production or ‘birth’ of
offspring.
• We can calculate generation time from a
life table:
Gc =
lxbxx
Ro
Calculating r from a life table:
Gc = 4.0/3.0 = 1.33 years
 lxbxx = 4.0
r=
loge(R0)
G
=
loge(3.0)
1.33
= 0.824 per individual per year
r > 0 population increasing, r = 0 population stable,
r < 0 population decreasing
lx = proportion of original individuals surviving to
each age class.
bx = number of offspring produced per individual for the
given age class (often refers to females only)
R0 = net reproductive output (lxbx)
> 1 pop increasing, = 1 pop stable, < 1 pop decreasing
Gives us a multiplier to see how much the population
increases each generation
Gc = generation time
this is an approximation because not all births
occur at once.
r
= the populations intrinsic capacity for increase
each r is for a specific set of environmental conditions
environmental conditions may affect
survival/reproduction
> 0 pop increasing, = 0 pop stable, < 0 pop decreasing
Temperature and moisture
effects on r value for a
wheat beetle (Store wheat
in cool dry place).
Comparison of r value’s
for two species of wheat
beetle.
Species With a High r
• Are not necessarily more common
• However, these species can recover more
quickly from disturbances
Increasing r: r = R0/G
1) Reduction in age at first reproduction
–
Basically reduce generation time
Age at First Breeding
# for r = 0.76
1
15
2
32
3
67
4
141 (actual)
5
297
6
564
2) Increase the number of progeny in each
reproductive event
–
Increases R0
3) Increase the number of reproductive events
–
Increase in longevity essentially increases R0
About r
• r is an oversimplification of nature
– We do not find populations with a stable age
distribution or with constant age-specific
mortality and fertility rates
• Actual population increases we observed
varies in more complex ways than the
theoretical r
• However, the importance of r lies mostly in
its use as a model for comparison with the
actual rates of increase we see in nature
– Can be used to assess environmental quality
Reproductive Value
• Reproductive value – the contribution to
the future population that an individual
will make
• In a stable population reproductive value
at age x =
w
Vx = 
t=x
ltbt
lx
w
or

Vx = bx + t=x+1
t and x are age and w is age of last reproduction
ltbt
lx
Females begin breeding
Males protect harems
Present progeny
Vx = bx +
Residual reproductive value
= number of progeny that
on average will be
ltbt
produced in the rest of an
individuals lifetime
l
x
If the population is growing (not stable), then this
value must be discounted because the value of one
progeny is less in a larger population.
Reproductive value is important in the evolution of
life-history traits because natural selection acts more
strongly on age classes with high reproductive
values (cancer in humans).
Predation has more of an effect if acting on
individuals with high reproductive value.
Age Distributions
• Stable age distribution – age-specific
fertility and mortality are fixed and the
population grows exponentially.
• Stationary age distribution – when the
fertility rate exactly equals the mortality
rate and the population does not change
in size over time.
• Populations are almost never stable so we
never find a stable age distribution or a
stationary age distribution.
Relationships
Natality Rates
Environmental
factors
Age
Composition
Mortality Rates
Rate of increase
or decrease of
the population
Age Distribution
• Increasing populations have a predominance of
young organisms, whereas stable or declining
populations do not
Populations of
vole grown in
the lab.
Judging the Status of the 1995
Human Population
Age structure can differ strongly year to year in plant and
animal species (dominant fish year classes).
Neither has an age
structure
representative of a
stable age distribution.
Reproductive Strategies
• Big-bang reproduction (semelparity) –
reproduce once in a lifetime
– Salmon – spawn once and die
• Repeated reproduction (iteroparity) –
reproduce more than once in a lifetime
– Oak tree – may drop thousands of acorns for
200 years or more
• Why have different life cycles evolved?
Reproduction Tradeoffs
At high levels of
reproductive effort, a
small increase in effort
is more beneficial for
big-bang reproduction
than for repeated
reproduction
• The key demographic effect of big-bang
reproduction is higher reproductive rates.
– Plants that reproduce only once produce 2 – 5 as many
seeds as closely related species that reproduce
repeatedly
– Big-bang reproducers usually have a similar r as similar
species that are repeat reproducers
• Repeated reproduction is favored when
– Adult survival rates are high
– Juvenile survival is highly variable
• Repeated reproduction spreads the risk of
reproducing over a longer time period and thus
acts as an adaptation that thwarts environmental
fluctuations.
– If conditions are bad this year, then reproduce next year.
Repeated reproduction may be an evolutionary
response to uncertain survival from zygote to
adult stages.
Long Life Span
Short Life Span
Steady Reproductive
Success
?
Possible
Variable Reproductive
Success
Possible
Not Possible
Growth With Discrete Generations
• Species with a single annual breeding season
and a life span of one year (ex. annual plants).
• Population growth can then be described by the
following equation:
Nt+1 = R0Nt
• Where
– Nt = population size of females at generation t
– Nt+1 = population size of females at generation t + 1
– R0 = net reproductive rate, or number of female offspring
produced per female generation
• Population growth is very dependent on R0
Multiplication Rate (R0) Constant
• If R0 > 1, the population increases geometrically
without limit. If R0 < 1 then the population
decreases to extinction.
• The greater R0 is the faster the population
Geometric Growth
increases:
Multiplication Rate (R0) Dependent
on Population Size
• Carrying Capacity – the maximum population size
that a particular environment is able to maintain
for a given period.
– At population sizes greater than the carrying capacity,
the population decreases
– At population sizes less than the carrying capacity, the
population increases
– At population sizes = the carrying capacity, the
population is stable
• Equilibrium Point – the population density that =
the carrying capacity.
Net Reproductive rate (R0) as a
function of population density:
Y = mX + b
Y = b – m(X)
N = 100, then R0 = 1.0
population stable
N > 100, then R0 < 1.0
population decreases
Intercept
N < 100, then R0 > 1.0
population increases
Remember, at R0 = 1.0
birth rates = death
rates
• We can measure population size in terms of deviation
from the equilibrium density:
z = N – Neq
Where:
z = deviation from equilibrium density
N = observed population size
Neq = equilibrium population size (R0 = 1.0)
• R0 = 1.0 – B(N – Neq) ( When N = Neq then R0 = 1.0)
Where:
R0 = net reproductive rate
y-intercept (b) will always = 1.0; population is
stable
(-)B = slope of line (m; the B comes from a
regression coefficient.
With these equations:
z = N – Neq
R0 = 1.0 – B(N – Neq)
We can substitute R0 in Nt+1 = R0Nt to get:
Nt+1 = [1.0 – B(zt)]Nt
How much the
population will
change (R0)
Start with an initial population (Nt) of 10, a slope (B) =
0.011, and Neq = 100, and the population gradually
reaches 100 and stays there.
Nt+1 = [1.0 – B(z)]Nt
10.00
19.90
37.43
63.20
88.78
99.74
100.03
100.00
100.00
100.00
100.00
100.00
120
100
Population Size
1
2
3
4
5
6
7
8
9
10
11
12
The population reaches
stabilization with a smooth
approach.
80
60
40
20
0
1
2
3
4
5
6
7
Generation
8
9
10
11
12
10.00
2
26.20
3
61.00
4
103.82
5
96.68
6
102.46
7
97.92
8
101.58
9
98.69
10
101.02
11
99.17
12
100.65
13
99.47
14
100.42
15
99.66
16
100.27
17
99.78
18
100.17
19
99.86
20
100.11
Start with an initial population (Nt) of 10, a slope
(B) = 0.018, and Neq = 100, and the population
oscillates a little bit but eventually (64
generations) stabilizes at 100 and stays there.
This is called convergent oscillation.
Nt+1 = [1.0 – B(z)]Nt
Population Size
1
120
100
80
60
40
20
0
1
3
5
7
9
11
13
Generation
15
17
19
10.00
2
32.50
3
87.34
4
114.98
5
71.92
6
122.41
7
53.84
8
115.97
9
69.67
10
122.50
11
53.60
12
115.78
13
70.11
14
122.50
15
53.59
16
115.77
17
70.12
18
122.50
19
53.59
20
115.77
Start with an initial population (Nt) of 10, a slope
(B) = 0.025, and Neq = 100, and the population
oscillates with a stable limit cycle that continues
indefinitely.
Nt+1 = [1.0 – B(z)]Nt
150
Population
1
100
50
0
1
3
5
7
9
11
13
Generation
15
17
19
10.00
2
36.10
3
103.00
4
94.05
5
110.29
6
77.39
7
128.13
8
23.59
9
75.87
10
128.96
11
20.64
12
68.14
13
131.10
14
12.87
15
45.40
16
117.28
17
58.51
18
128.91
19
20.84
20
68.68
Start with an initial population (Nt) of 10, a slope
(B) = 0.029, and Neq = 100, and the population
fluctuates chaotically.
Nt+1 = [1.0 – B(z)]Nt
150
Population
1
100
50
0
1
3
5
7
9
11
13
Generation
15
17
19
B
0.011
0.018
Population
Gradually approaches equilibrium
Convergent oscillation
0.025
0.029
Stable limit cycles
Chaotic fluctuation
As the slope increases, the population fluctuates
more. A high B causes an ‘overshoot’ towards
stabilization. Remember: B is the slope of the line
and represents how much Y changes for each
change in X.
• Define L as B(Neq): The response of the
population at equilibrium
– L between 0 and 1
 Population approaches equilibrium without
oscillations
– L between 1and 2
 Population undergoes convergent
oscillations
– L between 2 and 2.57
 Population exhibits stable limit cycles
– L above 2.57
 Population fluctuates chaotically
Growth With Overlapping Generations
• Previous examples were for species that
live for a year, reproduce then die.
• For populations that have a continuous
breeding season, or prolonged
reproductive period, we can describe
population growth more easily with
differential equations.
Multiplication Rate Constant
• In a given population, suppose the
probability of reproducing (b) is equal to
the probability of dying (d).
– r=b–d
Nt
rt
– Then rN = (b – d)N 
=
e
N0
– Where:
 Nt = population at time t
 t = time
 r = per-capita rate of population growth
 b = instantaneous birth rate
 d = instantaneous death rate
– Population grows geometrically
We can determine how long it will take for a population
to double:
Nt
rt
=
2
=
e
N0
Loge(2) = rt
Loge(2) / r = t; r = realized rate of population growth per capita
For example:
r
t
0.01
69.3
0.02
34.7
0.03
23.1
0.04
17.3
0.05
13.9
0.06
11.6
Multiplication Rate Dependent on
Population Size
dN
K-N
= rN
dt
K
Where:
N = population size
t = time
r = intrinsic capacity for increase
K = maximal value of N (‘carrying capacity’)
r
K
Pop. Size (K-N)/K
Growth Rate
1.0
1
99/100
0.99
1.0
50
50/100
25.00
1.0
75
25/100
18.75
1.0
95
5/100
4.75
1.0
99
1/100
0.99
1.0
100
0/100
0.00
Logistic population growth has
been demonstrated in the lab.
Year-to-year environmental fluctuations are one
reason that population growth can not be
described by the simple logistic equation.
Time-Lag Models
• Animals and plants do not respond immediately
to environmental conditions.
• Change our assumptions so that a population
responds to t-1 population size, not the t
population size.
L=Bneq
If 0<L<0.25, then stable
equilibrium with no
oscillation
If 0.25<L<1.0, then
convergent oscillation
If L > 1.0, then stable
limit cycles or divergent
oscillation to extinction
Stochastic Models
• Models discussed so far are deterministic:
given certain conditions, each model
predicts one exact condition.
• However, biological systems are
probabilistic:
– what is the probability that a female will have a
litter in the next unit of time?
– What is the probability that a female will have a
litter of three instead of four?
• Natural population trends are the joint
outcome of many individual probabilities
• These probabilistic models are called
stochastic models.
Basic Nature of Stochastic Models
• Nt+1 = R0Nt
• If R0 = 2, then a population size of 6 will yield a
population of 12 in one generation according to a
deterministic model: Nt+1 = 2(6) = 12
• Suppose our stochastic model says that a female
has an equal probability of having 1 or 3 offspring
(average = 2; so R0 = 2):
Probability
One female offspring
Three female offspring
0.5
0.5
• Since the number of offspring is random, we can
flip a coin and heads = 1 offspring, tails = 3
offspring to determine the total number of
offspring produced:
Outcome
Parent
Trial 1
Trial 2
Trial 3
Trial 4
1
(h)1
(t)3
(h)1
(t)3
2
(t)3
(h)1
(t)3
(h)1
3
(h)1
(t)3
(h)1
(h)1
4
(t)3
(t)3
(t)3
(t)3
5
(t)3
(t)3
(t)3
(h)1
6
(t)3
(t)3
(h)1
(h)1
14
16
12
10
Total population in next
generation:
Frequency Distribution After Several Trials
• Although the most common population size is
twelve as expected, the population could be any
size from 6 to 18.
Population Projection Matrices
• Used to calculate population changes from agespecific (or stage specific) birth and survival
rates.
– Can estimate how population growth will respond to
changes in only one specific age class.
F = fecundity
P = probability of surviving
and moving to next age
class
F = fecundity
Age Based
P = probability of surviving
and staying in same stage
G = probability of moving
to next stage
Stage Based
Stage-based life table and fecundity table for the loggerhead
sea turtle. #’s assume a 3% population decline / year.
Class
Size
Approx.
Age
1
Eggs,
hatchlings
<10
<1
0.6747
0
2
Small Juv.
10.1 – 58.0
1-7
0.7857
0
3
Large Juv.
58.1 – 80.0
8-15
0.6758
0
4
Subadults
80.1 – 87.0
16-21
0.7425
0
5
Novice
Breeders
>87.0
22
0.8091
127
6
1st year
remigrants
>87.0
23
0.8091
4
7
Mature
breeder
>87.0
24-54
0.8091
80
Stage #
Annual
survivorship
Fecundity
(eggs/yr)
Matrix Model
P1
F2
F3
F4
F5
F6
F7
G1
P2
0
0
0
0
0
0
G2
P3
0
0
0
0
0
0
G3
P4
0
0
0
0
0
0
G4
P5
0
0
0
0
0
0
G5
P6
0
0
0
0
0
0
G6
P7
Pi = proportion of that stage that remains in that stage
Gi = proportion of that stage that moves to the next stage
Fi = specific fecundity for that stage
Stage #
Approx.
Annual
Fecundity
Age
survivorship (eggs/yr)
1
<1
0.6747
0
2
1-7
0.7857
0
3
8-15
0.6758
0
4
16-21
0.7425
0
5
22
0.8091
127
6
23
0.8091
4
7
24-54
0.8091
80
0.7370
= P2
0.0487 = G2
0.7857 = P2 + G2
1
2
3
4
5
6
7
0
0
0
0
127
4
80
0
0
0
0
0
0
0
0
0
0
0
0
0.6747 0.7370
0
0.0487 0.6610
0
0
0.0147 0.6907
0
0
0
0.0518
0
0
0
0
0
0
0
0.8091
0
0
0
0
0
0
0
0.8091 0.8089
= Stage #
P1
F2
F3
F4
F5
F6
F7
N1
G1
P2
0
0
0
0
0
N2
0
G2
P3
0
0
0
0
N3
0
0
G3
P4
0
0
0
0
0
0
G4
P5
0
0
N5
0
0
0
0
G5
P6
0
N6
0
0
0
0
0
G6
P7
N7
X
N4
=
N1
= (P1*N1) + (F2*N2) + (F3*N3) + (F4*N4) + (F5*N5) + (F6*N6) + (F7*N7)
N2
= (G1*N1) + (P2*N2) + (0*N3) + (0*N4) + (0*N5) + (0*N6) + (0*N7)
N3
= (0*N1) + (G2*N2) + (P3*N3) + (0*N4) + (0*N5) + (0*N6) + (0*N7)
N4
= (0*N1) + (0*N2) + (G3*N3) + (P4*N4) + (0*N5) + (0*N6) + (0*N7)
N5
= (0*N1) + (0*N2) + (0*N3) + (G4*N4) + (P5*N5) + (0*N6) + (0*N7)
N6
= (0*N1) + (0*N2) + (0*N3) + (0*N4) + (G5*N5) + (P6*N6) + (0*N7)
N7
= (0*N1) + (0*N2) + (0*N3) + (0*N4) + (0*N5) + (G6*N6) + (P7*N7)
• With matrix models, we can simulate an
increase or decrease in survival or
fecundity and then determine what effect
that will have on population growth.
• So what? Well, we can determine what
age class or stage is most important to
population growth for an endangered
species.
By either increasing fecundity by 50% or survival to
100%, we can see that large juvenile survival is most
important to population growth, so put your
management efforts towards protecting large juveniles.