* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Survey
Document related concepts
Transcript
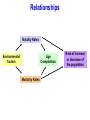
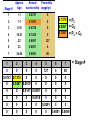
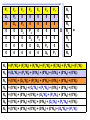
Population Dynamics Population – a group of organisms of the same species occupying a particular space at a particular time. Demes – groups of interbreeding organisms • local population • smallest collective unit of a plant or animal population Populations are units of study. Population Attributes • Density – number of organisms per unit area or per unit volume • Affected by: – Natality – the reproductive output (birth rate) of a population – Mortality – the death rate of organisms in a population – Immigration – number of organisms moving into the area occupied by the population – Emigration – number of organisms moving out of the area occupied by the population Population Density Four primary population parameters: Unitary and Modular Organisms • Unitary organisms – individual units such as humans or mice • Modular organisms – organisms that do not come in simple units of individuals – Several grasses that are attached by runners Density Examples Two fundamental attributes that affect our choice of techniques for population estimation are the size and mobility of the organism with respect to humans. Abundance and Animal Size Birds are less abundant than mammals of equivalent size. Density Relationships Two Types of Density Estimates • Absolute Density – a known density such as #/m2 • Relative Density – we know when one area has more individuals than another Measuring Absolute Density • Total Count – count the number of organisms living in an area – Human census, number of oak trees in a wooded lot, number of singing birds in an area – Total counts generally are not used very often • Sampling Methods – use a sample to estimate population size – Either use the quadrat or capture-recapture method Quadrat Method • A Quadrat is a sampling area of any shape randomly deployed. Each individual within the quadrat is counted and those numbers are used to extrapolate population size. – Example: a 100 square centimeter metal rectangle is randomly thrown four times and all of the beetles of a particular species within the square are counted each time: 19, 21, 17, and 19. This translates to 19 beetles per 100 cm2 or 1900 per m2. Transects as Quadrats • Each transect was 110 meters long and 2m wide (220 m2 or 0.022/ha). All trees taller than 25 cm counted. Capture-recapture Method • Important tool for estimating density, birth rate, and death rate for mobile animals. • Method: – Collect a sample of individuals, mark them, and then release them – After a period, collect more individuals from the wild and count the number that have marks – We assume that a sample, if random, will contain the same proportion of marked individuals as the population does – Estimate population density Peterson Method Marked animals in second sample Total caught in second sample 5 = 16 20 N = Marked animals in first sample Total population size N = 64 Assumptions For All CaptureRecapture Studies • Marked and unmarked animals are captured randomly. • Marked animals are subject to the same mortality rates as unmarked animals. The Peterson method assumes no mortality during the sampling period. • Marked animals are neither lost or overlooked. Indices of Relative Density • Assume that samples represent some relatively constant but unknown relationship to total population size. – # cars in the Piggly Wiggly parking lot • Provides an index of abundance – Is population increasing, decreasing, or staying the same – Are there more animals in one location than another? – Can not quantify differences between sites Twice the number of tracks does not = twice as many animals Some Indices Used • Traps • Number of Fecal Pellets • Vocalization Frequency • Pelt Records • Catch per Unit Fishing Effort • • • • • Number of Artifacts Questionnaires Cover Feeding Capacity Roadside Counts Natality • Fecundity – physiological notion that refers to an organism’s potential reproductive potential – Usually inversely proportional to the amount of parental care given to young • Fertility – Ecological concept that is based on the number of viable offspring produced during a specific period – Realized fertility – actual fertility rate One birth per 15 years per human female in the child-bearing ages – Potential fertility – potential fertility rate One birth per 10 to 11 months per human female in the child-bearing ages Mortality • Opposite of mortality is survival • Longevity focuses on the age of death of individuals in a population – Potential longevity – maximum lifespan by an individual of a particular species Set by the organisms physiology (dies of old age) Sometimes described as the average longevity of individuals living in optimal conditions – Realized longevity – actual life span of an organism Measured as an average for all animals living under real environmental conditions Determining Mortality • Mark several individuals and measure how many survive from time t to t+1. • If abundance of successive age groups is known, then you can estimate mortality between successive age groups. • Can use catch curves for fish: Survival between age 2 and 3= 147/292=0.50 Or develop regression equation 292 147 Immigration and Emigration • Seldom measured • Assumed to be equal or insignificant (island pop’s) • However, dispersal may be a critical parameter in population changes Limitations of the Population Approach • How to determine what exactly is a population – How clear are the boundaries? • Population does not exist as an isolate – Individuals interact with other members of the community Life Tables - Mortality • Mortality is one of the four key parameters that drive population changes. • We can use a life table to answer particular questions about population mortality rates. – What life stage has the highest mortality? – Do older organisms die more frequently than young organisms • A cohort life table is an age-specific summary of the mortality rates operating on a cohort of individuals. • Cohort – a collective group of individuals – Fish year class, all mice born in March, tadpoles from a single frog, freshman year class Cohort Life Table: X = age nx = number alive at time t lx = proportion of organisms surviving from the start of the life table to age x (ex: l1 = n1/n0, 0.217 = 25/115; l2=n2/n0, 0.165=19/115) dx = number dying during the age interval x to x + 1 (ex:d0=n0-n1, 90 = 115-25; d1=n1-n2, 6=25-19) qx = per capita rate of mortality during the age interval x to x + 1 (ex: q0=d0/n0, 0.78 =90/115; q1=d1/n1) Formula’s For Cohort Life Table • X = age group we decide on • nx = observed • lx = lx+1 = nx+1/nx (overall survival) • dx = nx - nx+1 (age specific number dying) • qx = dx / nx (age specific mortality rate) Per Capita Rates • Per capita is a presentation of data as a proportion of the population. • Suppose a disease kills 400 ducks: – If total duck population = 250,000 then the per capita mortality = 400/250,000 = 0.16%. – If total duck population = 2,500 then the per capita mortality = 400/2,500 = 16%. • Per capita gives us an idea of how the entire population is affected. Survivorship Curve A plot of nx on a Log scale from a starting cohort of 1,000 individuals. Three Types of General Curves Survival curve Examples of Each Type: •Type 1 – Humans •Type 2 – Birds •Type 3 - Fish These curves are models. Most real curves are intermediate. Mortality curve Static Life Table Calculated by taking a cross section of a population at a specific time: Per Capita Cohort Versus Static Life Tables • Cohort follows an individual cohort through time and static looks at all of the individuals currently present. • The two are equal if and only if the environment does not change from year to year and the population is at equilibrium. – The human cohort life table for 1900 does little good for predicting life expectancy for today. How to Collect Life Table Data 1) Survivorship directly observed. • • Follow an individual cohort through time at close intervals. Best to have since it generates a cohort life table directly and does not assume that the population is stable over time. Balanus can affect the survival of Chthamalus as determined by survivorship curve How to Collect Life Table Data 2) Age at Death Observed. • By determining how old individuals were when they died, we can create a life table. Based on 584 individuals plus observed estimated mortality for age 1 and 2 individuals How to Collect Life Table Data 3) Age Structure Directly Observed. • We can construct a life table based on the age structure of a population – • Counting rings on a tree or a fish otolith. Assume a constant age structure, which is hardly the case. Aging • Does mortality increase with age (senescence)? This data proves our simple theory of senescence is not correct Mortality Rate (qx) – Not for some Mediterranean fruit flies: Intrinsic Capacity For Increase In Numbers • By combining reproduction and mortality estimates, we can determine net population change (intrinsic capacity for increase). • The environment can influence population mean longevity or survival rate, natality rate, and growth rate. – Can be summed with natality and death rate Fertility Schedule Population net reproductive rate bx = natality 0.6% increase each generation (lx)(bx) = reproductive output for that age class R0 < 1 population is declining, R0 = 1 population is stable, R0 > population is increasing. Population Increase • If survival and fertility rates do not change, and no limit is placed on population growth – at what rate will a population increase? • It seems we need to know age-specific survival rates, age-specific fertility rates, and age structure – If all females in U.S. were >50 years old, no new young would be produced. • However, the age structure does not need to be known! Stable Age Distribution • Given constant schedule of natality and mortality rates, a population will eventually reach a stable age distribution, and will remain at this age distribution indefinitely. • Stable age distribution: – – – – 60% age 0 25% age 1 10% age 2 4% age 3 • Although the absolute number will change, the proportion of each age class remains constant! For Example This animal lives three years, produces two young at exactly one year, and one young at exactly year two, and no young year three, then dies at end of year 3. If a population starts with one individual at age 0, the age distribution quickly becomes stable: 60% age 0, 25% age 1, 10% age 2, and 4% age 3. Stable Age Distribution When a population has reached the stable age distribution, it will increase in numbers according to: dN = rN Written in integral form Nt = N0ert dt Nt = number of individuals at time t N0 = number of individuals at time 0 e = 2.71828 (a constant) r = intrinsic capacity for increase for the particular environmental conditions t = time This equation describes the curve of geometric increase in an expanding population (or geometric decrease to zero if r is negative). For Example: N0ert = Nt Any population on a fixed age schedule of natality and mortality will change geometrically. This geometric change will dictate a fixed and unchanging age distribution – the stable age distribution. Generation Time • Generation time – mean period elapsing between the production or ‘birth’ of parents and the production or ‘birth’ of offspring. • We can calculate generation time from a life table: Gc = lxbxx Ro Calculating r from a life table: Gc = 4.0/3.0 = 1.33 years lxbxx = 4.0 r= loge(R0) G = loge(3.0) 1.33 = 0.824 per individual per year r > 0 population increasing, r = 0 population stable, r < 0 population decreasing lx = proportion of original individuals surviving to each age class. bx = number of offspring produced per individual for the given age class (often refers to females only) R0 = net reproductive output (lxbx) > 1 pop increasing, = 1 pop stable, < 1 pop decreasing Gives us a multiplier to see how much the population increases each generation Gc = generation time this is an approximation because not all births occur at once. r = the populations intrinsic capacity for increase each r is for a specific set of environmental conditions environmental conditions may affect survival/reproduction > 0 pop increasing, = 0 pop stable, < 0 pop decreasing Temperature and moisture effects on r value for a wheat beetle (Store wheat in cool dry place). Comparison of r value’s for two species of wheat beetle. Species With a High r • Are not necessarily more common • However, these species can recover more quickly from disturbances Increasing r: r = R0/G 1) Reduction in age at first reproduction – Basically reduce generation time Age at First Breeding # for r = 0.76 1 15 2 32 3 67 4 141 (actual) 5 297 6 564 2) Increase the number of progeny in each reproductive event – Increases R0 3) Increase the number of reproductive events – Increase in longevity essentially increases R0 About r • r is an oversimplification of nature – We do not find populations with a stable age distribution or with constant age-specific mortality and fertility rates • Actual population increases we observed varies in more complex ways than the theoretical r • However, the importance of r lies mostly in its use as a model for comparison with the actual rates of increase we see in nature – Can be used to assess environmental quality Reproductive Value • Reproductive value – the contribution to the future population that an individual will make • In a stable population reproductive value at age x = w Vx = t=x ltbt lx w or Vx = bx + t=x+1 t and x are age and w is age of last reproduction ltbt lx Females begin breeding Males protect harems Present progeny Vx = bx + Residual reproductive value = number of progeny that on average will be ltbt produced in the rest of an individuals lifetime l x If the population is growing (not stable), then this value must be discounted because the value of one progeny is less in a larger population. Reproductive value is important in the evolution of life-history traits because natural selection acts more strongly on age classes with high reproductive values (cancer in humans). Predation has more of an effect if acting on individuals with high reproductive value. Age Distributions • Stable age distribution – age-specific fertility and mortality are fixed and the population grows exponentially. • Stationary age distribution – when the fertility rate exactly equals the mortality rate and the population does not change in size over time. • Populations are almost never stable so we never find a stable age distribution or a stationary age distribution. Relationships Natality Rates Environmental factors Age Composition Mortality Rates Rate of increase or decrease of the population Age Distribution • Increasing populations have a predominance of young organisms, whereas stable or declining populations do not Populations of vole grown in the lab. Judging the Status of the 1995 Human Population Age structure can differ strongly year to year in plant and animal species (dominant fish year classes). Neither has an age structure representative of a stable age distribution. Reproductive Strategies • Big-bang reproduction (semelparity) – reproduce once in a lifetime – Salmon – spawn once and die • Repeated reproduction (iteroparity) – reproduce more than once in a lifetime – Oak tree – may drop thousands of acorns for 200 years or more • Why have different life cycles evolved? Reproduction Tradeoffs At high levels of reproductive effort, a small increase in effort is more beneficial for big-bang reproduction than for repeated reproduction • The key demographic effect of big-bang reproduction is higher reproductive rates. – Plants that reproduce only once produce 2 – 5 as many seeds as closely related species that reproduce repeatedly – Big-bang reproducers usually have a similar r as similar species that are repeat reproducers • Repeated reproduction is favored when – Adult survival rates are high – Juvenile survival is highly variable • Repeated reproduction spreads the risk of reproducing over a longer time period and thus acts as an adaptation that thwarts environmental fluctuations. – If conditions are bad this year, then reproduce next year. Repeated reproduction may be an evolutionary response to uncertain survival from zygote to adult stages. Long Life Span Short Life Span Steady Reproductive Success ? Possible Variable Reproductive Success Possible Not Possible Growth With Discrete Generations • Species with a single annual breeding season and a life span of one year (ex. annual plants). • Population growth can then be described by the following equation: Nt+1 = R0Nt • Where – Nt = population size of females at generation t – Nt+1 = population size of females at generation t + 1 – R0 = net reproductive rate, or number of female offspring produced per female generation • Population growth is very dependent on R0 Multiplication Rate (R0) Constant • If R0 > 1, the population increases geometrically without limit. If R0 < 1 then the population decreases to extinction. • The greater R0 is the faster the population Geometric Growth increases: Multiplication Rate (R0) Dependent on Population Size • Carrying Capacity – the maximum population size that a particular environment is able to maintain for a given period. – At population sizes greater than the carrying capacity, the population decreases – At population sizes less than the carrying capacity, the population increases – At population sizes = the carrying capacity, the population is stable • Equilibrium Point – the population density that = the carrying capacity. Net Reproductive rate (R0) as a function of population density: Y = mX + b Y = b – m(X) N = 100, then R0 = 1.0 population stable N > 100, then R0 < 1.0 population decreases Intercept N < 100, then R0 > 1.0 population increases Remember, at R0 = 1.0 birth rates = death rates • We can measure population size in terms of deviation from the equilibrium density: z = N – Neq Where: z = deviation from equilibrium density N = observed population size Neq = equilibrium population size (R0 = 1.0) • R0 = 1.0 – B(N – Neq) ( When N = Neq then R0 = 1.0) Where: R0 = net reproductive rate y-intercept (b) will always = 1.0; population is stable (-)B = slope of line (m; the B comes from a regression coefficient. With these equations: z = N – Neq R0 = 1.0 – B(N – Neq) We can substitute R0 in Nt+1 = R0Nt to get: Nt+1 = [1.0 – B(zt)]Nt How much the population will change (R0) Start with an initial population (Nt) of 10, a slope (B) = 0.011, and Neq = 100, and the population gradually reaches 100 and stays there. Nt+1 = [1.0 – B(z)]Nt 10.00 19.90 37.43 63.20 88.78 99.74 100.03 100.00 100.00 100.00 100.00 100.00 120 100 Population Size 1 2 3 4 5 6 7 8 9 10 11 12 The population reaches stabilization with a smooth approach. 80 60 40 20 0 1 2 3 4 5 6 7 Generation 8 9 10 11 12 10.00 2 26.20 3 61.00 4 103.82 5 96.68 6 102.46 7 97.92 8 101.58 9 98.69 10 101.02 11 99.17 12 100.65 13 99.47 14 100.42 15 99.66 16 100.27 17 99.78 18 100.17 19 99.86 20 100.11 Start with an initial population (Nt) of 10, a slope (B) = 0.018, and Neq = 100, and the population oscillates a little bit but eventually (64 generations) stabilizes at 100 and stays there. This is called convergent oscillation. Nt+1 = [1.0 – B(z)]Nt Population Size 1 120 100 80 60 40 20 0 1 3 5 7 9 11 13 Generation 15 17 19 10.00 2 32.50 3 87.34 4 114.98 5 71.92 6 122.41 7 53.84 8 115.97 9 69.67 10 122.50 11 53.60 12 115.78 13 70.11 14 122.50 15 53.59 16 115.77 17 70.12 18 122.50 19 53.59 20 115.77 Start with an initial population (Nt) of 10, a slope (B) = 0.025, and Neq = 100, and the population oscillates with a stable limit cycle that continues indefinitely. Nt+1 = [1.0 – B(z)]Nt 150 Population 1 100 50 0 1 3 5 7 9 11 13 Generation 15 17 19 10.00 2 36.10 3 103.00 4 94.05 5 110.29 6 77.39 7 128.13 8 23.59 9 75.87 10 128.96 11 20.64 12 68.14 13 131.10 14 12.87 15 45.40 16 117.28 17 58.51 18 128.91 19 20.84 20 68.68 Start with an initial population (Nt) of 10, a slope (B) = 0.029, and Neq = 100, and the population fluctuates chaotically. Nt+1 = [1.0 – B(z)]Nt 150 Population 1 100 50 0 1 3 5 7 9 11 13 Generation 15 17 19 B 0.011 0.018 Population Gradually approaches equilibrium Convergent oscillation 0.025 0.029 Stable limit cycles Chaotic fluctuation As the slope increases, the population fluctuates more. A high B causes an ‘overshoot’ towards stabilization. Remember: B is the slope of the line and represents how much Y changes for each change in X. • Define L as B(Neq): The response of the population at equilibrium – L between 0 and 1 Population approaches equilibrium without oscillations – L between 1and 2 Population undergoes convergent oscillations – L between 2 and 2.57 Population exhibits stable limit cycles – L above 2.57 Population fluctuates chaotically Growth With Overlapping Generations • Previous examples were for species that live for a year, reproduce then die. • For populations that have a continuous breeding season, or prolonged reproductive period, we can describe population growth more easily with differential equations. Multiplication Rate Constant • In a given population, suppose the probability of reproducing (b) is equal to the probability of dying (d). – r=b–d Nt rt – Then rN = (b – d)N = e N0 – Where: Nt = population at time t t = time r = per-capita rate of population growth b = instantaneous birth rate d = instantaneous death rate – Population grows geometrically We can determine how long it will take for a population to double: Nt rt = 2 = e N0 Loge(2) = rt Loge(2) / r = t; r = realized rate of population growth per capita For example: r t 0.01 69.3 0.02 34.7 0.03 23.1 0.04 17.3 0.05 13.9 0.06 11.6 Multiplication Rate Dependent on Population Size dN K-N = rN dt K Where: N = population size t = time r = intrinsic capacity for increase K = maximal value of N (‘carrying capacity’) r K Pop. Size (K-N)/K Growth Rate 1.0 1 99/100 0.99 1.0 50 50/100 25.00 1.0 75 25/100 18.75 1.0 95 5/100 4.75 1.0 99 1/100 0.99 1.0 100 0/100 0.00 Logistic population growth has been demonstrated in the lab. Year-to-year environmental fluctuations are one reason that population growth can not be described by the simple logistic equation. Time-Lag Models • Animals and plants do not respond immediately to environmental conditions. • Change our assumptions so that a population responds to t-1 population size, not the t population size. L=Bneq If 0<L<0.25, then stable equilibrium with no oscillation If 0.25<L<1.0, then convergent oscillation If L > 1.0, then stable limit cycles or divergent oscillation to extinction Stochastic Models • Models discussed so far are deterministic: given certain conditions, each model predicts one exact condition. • However, biological systems are probabilistic: – what is the probability that a female will have a litter in the next unit of time? – What is the probability that a female will have a litter of three instead of four? • Natural population trends are the joint outcome of many individual probabilities • These probabilistic models are called stochastic models. Basic Nature of Stochastic Models • Nt+1 = R0Nt • If R0 = 2, then a population size of 6 will yield a population of 12 in one generation according to a deterministic model: Nt+1 = 2(6) = 12 • Suppose our stochastic model says that a female has an equal probability of having 1 or 3 offspring (average = 2; so R0 = 2): Probability One female offspring Three female offspring 0.5 0.5 • Since the number of offspring is random, we can flip a coin and heads = 1 offspring, tails = 3 offspring to determine the total number of offspring produced: Outcome Parent Trial 1 Trial 2 Trial 3 Trial 4 1 (h)1 (t)3 (h)1 (t)3 2 (t)3 (h)1 (t)3 (h)1 3 (h)1 (t)3 (h)1 (h)1 4 (t)3 (t)3 (t)3 (t)3 5 (t)3 (t)3 (t)3 (h)1 6 (t)3 (t)3 (h)1 (h)1 14 16 12 10 Total population in next generation: Frequency Distribution After Several Trials • Although the most common population size is twelve as expected, the population could be any size from 6 to 18. Population Projection Matrices • Used to calculate population changes from agespecific (or stage specific) birth and survival rates. – Can estimate how population growth will respond to changes in only one specific age class. F = fecundity P = probability of surviving and moving to next age class F = fecundity Age Based P = probability of surviving and staying in same stage G = probability of moving to next stage Stage Based Stage-based life table and fecundity table for the loggerhead sea turtle. #’s assume a 3% population decline / year. Class Size Approx. Age 1 Eggs, hatchlings <10 <1 0.6747 0 2 Small Juv. 10.1 – 58.0 1-7 0.7857 0 3 Large Juv. 58.1 – 80.0 8-15 0.6758 0 4 Subadults 80.1 – 87.0 16-21 0.7425 0 5 Novice Breeders >87.0 22 0.8091 127 6 1st year remigrants >87.0 23 0.8091 4 7 Mature breeder >87.0 24-54 0.8091 80 Stage # Annual survivorship Fecundity (eggs/yr) Matrix Model P1 F2 F3 F4 F5 F6 F7 G1 P2 0 0 0 0 0 0 G2 P3 0 0 0 0 0 0 G3 P4 0 0 0 0 0 0 G4 P5 0 0 0 0 0 0 G5 P6 0 0 0 0 0 0 G6 P7 Pi = proportion of that stage that remains in that stage Gi = proportion of that stage that moves to the next stage Fi = specific fecundity for that stage Stage # Approx. Annual Fecundity Age survivorship (eggs/yr) 1 <1 0.6747 0 2 1-7 0.7857 0 3 8-15 0.6758 0 4 16-21 0.7425 0 5 22 0.8091 127 6 23 0.8091 4 7 24-54 0.8091 80 0.7370 = P2 0.0487 = G2 0.7857 = P2 + G2 1 2 3 4 5 6 7 0 0 0 0 127 4 80 0 0 0 0 0 0 0 0 0 0 0 0 0.6747 0.7370 0 0.0487 0.6610 0 0 0.0147 0.6907 0 0 0 0.0518 0 0 0 0 0 0 0 0.8091 0 0 0 0 0 0 0 0.8091 0.8089 = Stage # P1 F2 F3 F4 F5 F6 F7 N1 G1 P2 0 0 0 0 0 N2 0 G2 P3 0 0 0 0 N3 0 0 G3 P4 0 0 0 0 0 0 G4 P5 0 0 N5 0 0 0 0 G5 P6 0 N6 0 0 0 0 0 G6 P7 N7 X N4 = N1 = (P1*N1) + (F2*N2) + (F3*N3) + (F4*N4) + (F5*N5) + (F6*N6) + (F7*N7) N2 = (G1*N1) + (P2*N2) + (0*N3) + (0*N4) + (0*N5) + (0*N6) + (0*N7) N3 = (0*N1) + (G2*N2) + (P3*N3) + (0*N4) + (0*N5) + (0*N6) + (0*N7) N4 = (0*N1) + (0*N2) + (G3*N3) + (P4*N4) + (0*N5) + (0*N6) + (0*N7) N5 = (0*N1) + (0*N2) + (0*N3) + (G4*N4) + (P5*N5) + (0*N6) + (0*N7) N6 = (0*N1) + (0*N2) + (0*N3) + (0*N4) + (G5*N5) + (P6*N6) + (0*N7) N7 = (0*N1) + (0*N2) + (0*N3) + (0*N4) + (0*N5) + (G6*N6) + (P7*N7) • With matrix models, we can simulate an increase or decrease in survival or fecundity and then determine what effect that will have on population growth. • So what? Well, we can determine what age class or stage is most important to population growth for an endangered species. By either increasing fecundity by 50% or survival to 100%, we can see that large juvenile survival is most important to population growth, so put your management efforts towards protecting large juveniles.