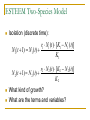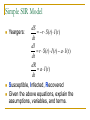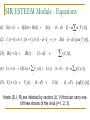Download Teaching Mathematics to Biologists and Biology to

Teaching Mathematics to
Biologists and Biology to
Mathematicians
Gretchen A. Koch
Goucher College
MathFest 2007
Introduction



Who: Undergraduate students and faculty
What: Improving quantitative skills of
students through combination of biology and
mathematics
When: Any biology or mathematics course


Simple examples interspersed throughout
semester
Common example as theme for entire semester
How??

Communication is key



Talk with colleagues in natural sciences
Use the same language
Make the connections obvious



Example: Why is Calculus I required for many biology
and chemistry majors??
Case studies, ESTEEM, and the BioQUEST
way
Have an open mind and be creative
What is a case study?


Imaginative story to introduce idea
Self-discovery with focus




Ask meaningful questions
Build on students’ previous knowledge
Students expand knowledge through research
and discussion.
Assessment
Case Studies – Beware of…





Clear objectives = easier assessment
Clear rubric = easier assessment
Focused questions = easier assessment
Too much focus = students look for the “right”
answer
Provide some starting resources



Continue building your database
Have clear expectations (Communication!)
Be flexible
Where do I start???
http://bioquest.org/icbl/
3
C:

Cal, Crabs, and the Chesapeake
Cal, a Chesapeake crabber, was sitting at the
end of the dock, looking forlorn. I
approached him and asked, “What’s the
matter, Cal?” He replied, “Hon – it’s just not
the same anymore. There are fewer and
fewer blue crabs in the traps each day. I just
don’t know how much longer I can keep the
business going. You’re a mathematician –
and you always say math is
everywhere…where’s the math in this???”
Case Analysis – Use for Discussion





What is this case about?
What could be causing the blue crab
population to decrease?
Can we predict what the blue crab population
will do?
Can we find data to show historic trends in
the blue crab population?
How will you answer these questions?
A Good Starting Place for Students
What do you know?
What do you need to know?
Learning Objectives - Mathematics

Use different mathematical models to explore
the population dynamics

Linear, exponential, and logistic growth models



Predator-prey model



Precalculus level
Continuous Growth ESTEEM Module
Calculus, Differential Equations, Numerical Methods
Two Species ESTEEM Module
SIR Model


Calculus, Differential Equations, Numerical Methods
SIR ESTEEM Module
Learning Objectives - Biology

Explore the reasons for the decrease in the
crab population







Habitat
Predators
Food Sources
Parasites
Invasive species
In field experiments
Journal reviews of ongoing experiments
Assessment and Evaluation Plan




Homework questions to demonstrate
understanding of use of ESTEEM modules
Homework questions to demonstrate
comprehension of topics presented in
ESTEEM modules
Group presentations of background
information
Exam questions to demonstrate synthesis of
mathematical concepts using different
examples
Sources



Blue Crab
Chesapeake Blue Crab Assessment 2005
Maryland Sea Grant The Living Chesapeake
Coast, Bay & Watershed Issues Blue Crabs
Blue Crab:
http://www.chesapeakebay.net/blue_crab.htm
But – what’s the answer??



Assessments and objectives vary
Knowledge of tools and structure
Adopt and adapt
Continuous Growth Models Module
First Growth Model

Suppose you ask Cal to keep track of the
number of crabs he catches for 10 days. He
gives you the following:
Day
1
2
3
4
5
6
7
8
9
10
Number
of Crabs
30
65
47
145
163
185
245
234
122
140

Do you see a pattern?
Linear Growth Model

Simplest model:
C (t  1)  C (t )  D

where C is the number of crabs on day t, and D is
some constant number.
Questions to ask:





What is D? Can you describe it in your own words?
What’s another form for this model?
Describe what this model means in terms of the crabs.
Does this model fit the data? Why or why not?
Is this model realistic?
ESTEEM Time!

Continuous Growth Module
Summary of Manipulations


Entered data in yellow areas
Clicked on “Plots-Size” tab


Manipulated parameters using sliders until fit
looked “right”
Asked questions about what makes it right
Exponential Growth Model

Simplest model:
C (t  1)  C (t )  r * C (t )

where C is the number of crabs on day t, and r is
some constant number.
Questions to ask:





What is r? Can you describe it in your own words?
What’s another form for this model?
Describe what this model means in terms of the crabs.
Does this model fit the data? Why or why not?
Is this model realistic?
ESTEEM Time!


Documentation
Continuous Growth Module
Compare the two models…



Why can the initial population be zero in the
linear growth model, but not in the
exponential growth model?
Why do such small changes in r make such a
big difference, but it takes large changes in D
to show a difference?
What do these models predict will happen to
the number of crabs that Cal catches in the
future?
Logistic Growth Model


Canonical model:
r * C (t ) * ( K  C (t ))
C (t  1)  C (t ) 
K
where C is the number of crabs on day t, and r and
K are constants.
Questions to ask:




What are r and K? Can you describe them in your own
words?
Describe what this model means in terms of the crabs.
Does this model fit the data? Why or why not?
Is this model realistic?
Further Analysis





What does the initial population need to be
for each of the three models to fit the data
well?
Why is the logistic model more realistic?
How did the parameters (D, r, K) affect the
models?
What does each model say about the total
capacity of Cal’s traps?
Do these models give an accurate prediction
of the future of the crab population?
Let’s kick it up a notch!

How do we model the entire crab population?


According to
http://www.chesapeakebay.net/blue_crab.htm,
blue crabs are predators of bivalves.
Cannibalism is correlated to the bivalve
population.
Predator-Prey Equations

Canonical example (Edelstein-Keshet):
dx
 ax  bxy
dt

dy
 cy  dxy
dt
Assumptions (pg 218):



Unlimited prey growth without predation
Predators only food source is prey.
Predator and prey will encounter each other.
Put it into context!
dx
 ax  bxy
dt
dy
  cy  dxy
dt
dB
  B B   B BC
dt
dC
  C C   C BC
dt
 i is the birth rate, and  i is the death rate for species i.
C (t ) is the population of crabs, while B( t ) is the population
of bivalves at time t.
What does this mean for the variables in the canonical
example? What do the terms mean?
Why does multiplication give likelihood of
an encounter ??

Law of Mass Action (Neuhauser)
 Given the following chemical reaction
A  B  AB,
the rate at which the product AB is produced by colliding
molecules of A and B is proportional to the concentrations of the
reactants.
rate = k [ A][ B ]

Translation to mathematics
 Rates = derivatives, k is a number
 What about [A] and [B]?
Another version

Cushing:
x '  x( r1  a11 x  a12 y )
y '  y( r2  a21 x )



What are the variables? Put them into
context.
What’s the extra term?
Did the assumptions change?
ESTEEM Two-Species Model

Isolation (discrete time):
r1  N1(t) [K1  N1(t)]
N1(t 1)  N1(t) 
K1
r2  N 2 (t) [K2  N 2(t)]
N 2(t 1)  N 2(t) 
K2


What kind of growth?
What are the terms and variables?
ESTEEM Two-Species Model
r1  N1 (t) [K1  N1 (t)  N 2 (t)]
N1(t 1)  N1 (t) 
K1

r2  N 2 (t) [K2  N 2 (t)  N 2 (t)]
N 2(t 1)  N 2 (t) 
K2
Discussion Questions






What do the terms mean?
Which species is the predator, which is the prey?
What other situations could these equations describe?
Why discrete time?
For what values of the rate constants does one species
inhibit the other? Have no effect? Have a positive effect?
Can we derive the continuous analogs?
ESTEEM Time!


Documentation
Two-Species Module
Summary of Manipulations



Use sliders to change values of parameters.
Examine all graphs.
Columns B and C have formulas for
numerical method.
Discussion Questions






How did one species affect the other?
What did the different graphs represent?
Did one species become extinct?
How can you have 1.25 crabs?
What would happen if there was a third
species? Write a general set of equations
(cases as relevant).
Can you determine the numerical method
used?
Simple SIR Model



dS
Yeargers:
  r  S (t )  I (t )
dt
dI
 r  S (t )  I (t )  a  I (t )
dt
dR
 a  I (t )
dt
Susceptible, Infected, Recovered
Given the above equations, explain the
assumptions, variables, and terms.
Connections to Case Study and Beyond

Possible ideas for research projects



Parasites and crabs
Is there a disease affecting the crab population?
Pick an epidemic, research it, and model it.



Analytical or numerical solutions
Make teams of biology majors and math majors.
ESTEEM module…
SIR ESTEEM Module - Equations
(1) S(t  1)  b[S(t)  R(t)] 
S(t)  (1 d)  [1   jV j (t)],
j
(2) I j (t  1)  b  I j (t)  I j (t)  (1 d  k j  rj ) 
(3) R (t  1) 
R(t)  (1 d)

S(t)  (1 d) [ jV j (t)],
 r I (t),
j
j
j
(4) U (t  1)  b[U (t)  V j (t)]  U (t)  (1 d )  [1    j I j (t)],
j
(5) V j (t  1) 
V j (t)  (1 d ) 
j
U (t)  (1 d )  [ j I j (t)].
Hosts (S, I, R) are infected by vectors (U, V) that can carry one
of three strains of the virus (i=1, 2, 3).
ESTEEM Time!


Documentation
SIR ESTEEM Module

Red boxes are for user entry.
SIR Module Discussion






Can you draw a diagram representing the SIR
model?
What are all of the variables and parameters in the
SIR model?
Can you find the continuous analog for the system?
Can you rewrite the system in matrix form?
What numerical method was used?
Why did some values of the parameters work, while
others did not?
Conclusion






Many, many ways to bring biology into the
classroom
Build on students’ intuition and knowledge
Make obvious connections between ideas
Don’t be afraid to try something new.
Experiment and experiment some more!
Have fun!
Works Consulted/Cited
Texts:
Cushing, J.M. (2004) Differential Equations: An Applied Approach. Pearson Prentice Hall.
Edelstein-Keshet, L. (1988) Mathematical Models in Biology. Birkhäuser.
Neuhauser, C. (2004) Calculus for Biology and Medicine. 2 ed. Pearson Education.
Yeargers, E.K., Shonkwiler, R.W., and J.V. Herod. (1996) An Introduction to the Mathematics of Biology with Computer Algebra
Models. Birkhäuser.
Online Sources:
BioQUEST Sources
BioQUEST: http://bioquest.org
ICBL: Investigative Case Based Learning: http://bioquest.org/icbl/
ESTEEM Module Documentation
Continuous Growth Models Documentation (John R. Jungck, Tia Johnson, Anton E. Weisstein, and Joshua Tusin):
http://www.bioquest.org/products/files/197_Growth_models.pdf
SIR Model Documentation (Tony Weisstein): http://www.bioquest.org/products/files/196_sirmodel.doc
Two Species Documentation (Tony Weisstein, Rene Salinas, John Jungck):
http://www.bioquest.org/products/files/203_TwoSpecies_Model.doc
Blue Crab Resources
Blue Crab: http://www.chesapeakebay.net/blue_crab.htm
Chesapeake Blue Crab Assessment 2005: http://hjort.cbl.umces.edu/crabs/Assessment05.html
Maryland Sea Grant The Living Chesapeake Coast, Bay & Watershed Issues Blue Crabs:
http://www.mdsg.umd.edu/issues/chesapeake/blue_crabs/index.html