Download Physics Beyond 2000

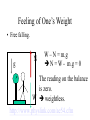
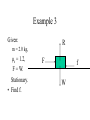
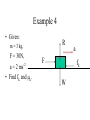
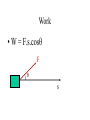
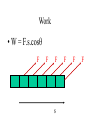
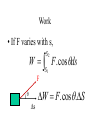
Physics Beyond 2000
Chapter 2
Newton’s Laws of Motion
Dynamics
• Concerned with the motion of bodies under
the action of forces.
• Bodies are assumed to have inertia.
• Momentum and force.
Momentum


p  m.v

p
•
= linear momentum of a body
• m = mass of the body

• v = velocity of the body
Momentum


p  m.v

p
•
= linear momentum of a body
• m = mass of the body

• v = velocity of the body
Momentum


p  m.v

p
•
= linear momentum of a body
• m = mass of the body

• v = velocity of the body

Note that p
Unit of p
is a vector quantity.
is
Momentum


p  m.v

p
•
= linear momentum of a body
• m = mass of the body

• v = velocity of the body

Note that p
Unit of p
is a vector quantity.
-1
is kg m s or N s.
Newton’s First Law of Motion
• A body continues in a state of rest or
uniform motion in a straight line unless
it is acted upon by external forces
Newton’s First Law of Motion
• A body continues in a state of rest or
uniform motion in a straight line unless
it is acted upon by external forces
The body changes its state of motion under
an external force.
Newton’s First Law of Motion
• A body continues in a state of rest or
uniform motion in a straight line unless
it is acted upon by external forces
The body does not change its state of motion
when there is not any external force.
Newton’s First Law of Motion
• A body continues in a state of rest or
uniform motion in a straight line unless
it is acted upon by external forces
The body changes its state of motion under
an external force.
Newton’s First Law of Motion
• A body continues in a state of rest or
uniform motion in a straight line unless
it is acted upon by external forces .
• Linear air track
– Vehicle without external force
– Vehicle under constant force
Inertia and Mass
• Inertia is a property of matter that causes it
to resist any change in its motion or to keep
its state of motion.
• Mass of a body is a quantitative measure of
its inertia.
• SI unit of mass: kg.
Newton’s Second Law of Motion
• The rate of change of momentum of a body
is proportional to and in the same direction
as the resultant force (net force) that acts on
it.


d
Fnet  (mv )
dt
Newton’s Second Law of Motion
• If the mass is a constant,


d
Fnet  (mv )
dt



dv
Fnet  m
 m.a
dt
Newton’s Second Law of Motion
• If the mass is a constant,



dv
Fnet  m
 m.a
dt


Fnet  kma
where k is a proportional constant
Newton’s Second Law of Motion
• If the mass is a constant,


Fnet  kma
where k is a proportional constant
In SI units, define 1 newton of force as the net
force acting on the mass of 1 kg and producing
-2
an acceleration
of 1 m s  k = 1 in SI units.
Newton’s Second Law of Motion
• If the mass is a constant,


Fnet  ma
a
m
where k = 1 in SI units
Note that the above equation is correct
on condition that SI units are used.
Fnet
Newton’s Second Law of Motion
• No matter the mass is a constant or not,


d
Fnet  (mv )
dt
Note that the above equation is correct
on condition that SI units are used.
Newton’s Second Law of Motion
• If F = 0,


d
Fnet  (mv )
dt
 mv = constant
 This is the case of Newton’s First
Law of Motion.
The origin of force
• Gravitational force
– Attraction between two massive particles.
• Electromagnetic force
– Electrostatic force: Force between two charged particles.
– Electromagnetic force: Force on a moving charged
particle in a magnetic field.
• Nuclear force
– Force between two the particles of the nucleus.
Weight
•
•
•
•
•
W = m.g
It is a gravitational force.
Use spring balance to measure the weight.
g varies on earth.
The measured value of g may be affected by
the rotation of the planet.
Normal Contact Force
The box is at rest on the ground.
N
W
N=W
Normal Contact Force
The box is at rest on the ground.
F
N
W
N=W+F
Normal Contact Force
The box is at rest on the ground.
F
N
W
N=W-F
Newton’s
rd
3
Law of Motion
• If one body exerts a force on another, there
is an equal and opposite force, called a
reaction, exerted on the first body by the
second.
A
B
Exerted on A by B.
Exerted on B by A.
Newton’s
rd
3
Law of Motion
are action and reaction pair
A
B
Exerted on A by B.
Exerted on B by A.
Newton’s
rd
3
Law of Motion
• Are they action and reaction pair?
Feeling of One’s Weight
• A man is standing on a balance inside a lift.
Feeling of One’s Weight
• What are the forces acting on the man?
Normal contact force N.
This is the reading on the
balance.
weight W = mg
Feeling of One’s Weight
• The net force and the acceleration. Newton’s 2nd
law of motion.
a
N
net force
F = N – W = m.a
m = mass
of the man
W
Feeling of One’s Weight
• The lift is moving up/down at constant speed or at
rest.
N
a=0
N – W = 0
N=W
The reading on the balance
W is the weight of the man.
Feeling of One’s Weight
• Moving up with acceleration or
• Moving down with retardation.
a
N
N – W = m.a
 N = W + m.a
The reading on the balance
is bigger than the weight
W
of the man.
Feeling of One’s Weight
• Moving up with retardation or
• Moving down with acceleration.
a
N
W – N = m.a
 N = W - m.a
The reading on the balance
is less than the weight
W of the man.
Feeling of One’s Weight
• Free falling.
g
N
W – N = m.g
 N = W - m.g = 0
The reading on the balance
is zero.
W  weightless.
http://www.physlink.com/ae54.cfm
Momentum and Impulse
• Impulse J = F.t
– F is the force
– t is the time for the force to act
Momentum and Impulse
• If a force F acts on an object of mass m for
a time t and changes its velocity from u to v,
prove that
J = mv – mu (i.e. mv) .
u
F F
F
m m
v
F
m
F
m
m
Momentum and Impulse
• If a force F acts on an object of mass m for
a time t and changes its velocity from u to v,
prove that
J = mv – mu (i.e. mv) .
v
F
m
Impulse and F - t graph
• The area under F-t
graph gives the
impulse as long as
the mass does not
change.
F
0
t
Examples of Impulse
• Catching a baseball
– Momentum of the baseball decreases to zero.
– Increase the time of action and reduce the force.
http://www.exploratorium.com/sports/
Examples of Impulse
• Catching a baseball
– Momentum of the baseball decreases to zero.
– Increase the time of action and reduce the force.
momentum
of the base
ball
time of contact
t
Examples of Impulse
• Catching a baseball
momentum
of the base
ball
mu
0  mu
F
t
time of action
t
t
Examples of Impulse
• Catching a baseball
– Momentum of the baseball decreases to zero.
– Increase the time of action and reduce the force.
FFF
Examples of Impulse
• Striking a tennis ball
• Go to the search engine
http://www.askjeeves.com
• and type the word “ tennis science “.
Examples of Impulse
• Use of a seat belt
– Reduce the force on the passenger by
prolonging the time of stopping the passenger
on crash.
F
Without seat belt
With seat belt
t
http://www.inel.gov/resources/ep/physics.html
Raindrops versus Hailstones
• Try to study the passage by yourself.
• Discuss with your classmates.
Example 1
•
•
•
•
•
Write the symbol for 0.14 kg.
1
ms
Write the symbol for 30
1
ms
Write the symbol for 50
Write the symbol for the impulse.
What is the formula connecting the above
quantities?
Note the
directions!
Example 1
What is the formula connecting the force and
the action time?
Momentum
of the ball
Example 1
time of action
0
time
Note the
directions!
Collisions
• Studying different kinds of collisions.
– Perfectly elastic collision.
– Completely inelastic collision.
– Collision in-between
• http://webphysics.ph.msstate.edu/javamirror/Default.html
Principle of conservation of
momentum
• When bodies in a system interact, the total
momentum remains constant, provided no
external force acts on the system.
Principle of conservation of
momentum
• When bodies in a system interact, the total
momentum remains constant, provided no
external force acts on the system.
• Before collision,
– Total momentum = m1.u1 + m2.u2
u1
m1
u2
m2
Principle of conservation of
momentum
• When bodies in a system interact, the total
momentum remains constant, provided no
external force acts on the system.
• Before collision,
– Total momentum = m1.u1 + m2.u2
u2u2u2
u2u2u2
u1 u1 u1 u1 u1
u1
m1 m1 m1 m1 m1m2
m2
m1
m2
m2
m2
m2
Principle of conservation of
momentum
• When bodies in a system interact, the total
momentum remains constant, provided no
external force acts on the system.
• After collision,
– Total momentum = m1.v1 + m2.v2
v2v2v2 v2
v1
v1
v1
v1
m1
m1
m1
m1m2m2m2m2
Principle of conservation of
momentum
• When bodies in a system interact, the total
momentum remains constant, provided no
external force acts on the system.
• Without external force,
m1.u1 + m2.u2 = m1.v1 + m2.v2
u1
m1
u2
m2
v1
m1
v2
m2
Principle of conservation of
momentum
The momentum of m1
time of action
m1.u1
m1v1
time
u1
m1
u2
m2
v1
m1
v2
m2
Principle of conservation of
momentum
The momentum of m2
time of action
m2.v2
m2.u2
time
u1
m1
u2
m2
v1
m1
v2
m2
Principle of conservation of
momentum
• For N bodies in collision.
Without external force,
sum of momenta before = sum of momenta after
N
N
m u  m v
i 0
i i
i 0
i i
Collisions in 2-dimension
• The collision is not head-on.
• The collision is oblique.
• Resolve each momentum into 2
perpendicular components (x- and ycomponents).
• Without external force, the momenta is
conserved along x-direction.
Without external force, the momenta is
conserved along y-direction.
Collisions in 2-dimension
Right-angled fork
• Two equal masses in oblique and elastic
collision.
• Before collision, one mass is stationary and
the other mass is moving.
• After collision, they move out in directions
perpendicular to each other.
Collisions in 2-dimension
Right-angled fork
• Two equal masses in oblique and elastic
collision.
• Before collision, one mass is stationary and
the other mass is moving.
• After collision, they move out in directions
perpendicular to each other.
Collisions in 2-dimension
Right-angled fork
• Two equal masses in oblique and elastic
collision.
• Before collision, one mass is stationary and
the other mass is moving.
• After collision, they move out in directions
perpendicular to each other.
Collisions in 2-dimension
Right-angled fork
• Two equal masses in oblique and elastic
collision.
• Before collision, one mass is stationary and
the other mass is moving.
• After collision, they move out in directions
perpendicular to each other.
Collisions in 2-dimension
Right-angled fork
Prove : After collision, they move out in
directions perpendicular to each other.
θ+φ= 900
mu
mv2
θ
ψ
mv1
Hint: Use conservation of momentum.
Use conservation of kinetic energy.
Collisions in 2-dimension
Right-angled fork
Example: α-particle colliding with helium
atom.
θ+φ= 900
mu
mv2
θ
ψ
mv1
Collisions in 2-dimension
Two unequal masses in oblique and elastic collision.
Before collision, one mass is stationary and the other
mass is moving.
m1u
m2v2
θ
ψ
m1v1
If m1>m2, then θ+ψ<90o
Collisions in 2-dimension
Two unequal masses in oblique and elastic collision.
Before collision, one mass is stationary and the other
mass is moving.
m1u
m2v2
θ
ψ
m1v1
If m1<m2, then θ+ψ>90o
Friction
• To act along the common surface between two
bodies in contact.
• To resist the relative motion (or tendency of
relative motion) of two bodies.
direction of motion
direction of friction
f
Friction
• To act along the common surface between two
bodies in contact.
• To resist the relative motion (or tendency of
relative motion) of two bodies.
direction of motion
f
direction of friction
Friction
• Static friction :
– The object is stationary.
• Kinetic friction :
– The object is moving.
Static Friction
• To resist the tendency of relative motion of
two bodies.
• Static friction has a maximum value,
limiting frictional force fL .
F
tendency of motion
in this direction
direction of static friction
f
F = f. The object is stationary.
Static Friction
• Static friction has a maximum value, limiting
frictional force fL .
• fL depends on the nature of the surface and normal
reaction.
• fL = μs.R where μs is the coefficient of static
friction.
R= normal reaction
F
direction of static friction
f
Kinetic Friction
• Kinetic frictional force fk is almost a constant.
• fk depends on the nature of the surface and normal
reaction.
• fk = μk .R where μk is the coefficient of kinetic
friction.
• fk < fL
F
R= normal reaction
direction of motion
direction of kinetic friction
fk
Chang of friction
fk
Gradually increase the applied force F
f
kinetic
static
fL
f=F
F
0
F
f
Example 3
Given:
R
m = 2.0 kg,
μs = 1.2,
F = W.
Stationary.
• Find f.
F
f
W
Example 4
• Given:
R
m = 3 kg,
F = 30N,
a = 2 ms-2 .
• Find fk and μk.
F
a
fk
W
Example 5
• Gradually
increase the
angle of
inclination.
Example 5
• Express f in
terms of W and
θ when the
object is still
stationary.
• What is the
maximum angle
θ if coefficient
of static friction
is μs?
R
f
θ
W
Friction
•
•
•
•
Cause of friction
Reducing friction
Role of friction
Friction in a car
Spring and force constant
• Hooke’s law
In equilibrium
– The extension or
compression of a spring
is proportional to the
force acting on it,
provided it does not
exceed the elastic limit.
e
• F = k.e
– where k is the force
constant of the spring
– and e is the extension
F
Spring and force constant
• Example 6
Combination of springs
• In series
k1
k2
F
• In parallel
k1
F
k2
Combination of springs
• In series
k1
k2
e
k1k 2
F
.e
k1  k 2
F
Combination of springs
• In parallel
k1
k2
F = (k1 + k2).e
e
F
Work and Energy
• Work is the transfer of energy.
Work
• W = F.s.cos
F

s
Work
• W = F.s.cos
F
F
F
s
F
F
F
Work
• W = F.s.cos
F

s
Note that F.cos is the component of F in the
direction of s.
Work
• If F varies with s,
S2
W   F . cos ds
S1
F

s
W  F. cos .S
Sign of Work done
• Free falling
– F is the gravitational force
to do work.
– Work done is positive.
– The ball gains K.E.
F
F s
F
Sign of Work done
• Moving up an object
at steady speed
– Apply an upward
force F to do work.
– Work done by F is
positive.
– The object gains
gravitational P.E.
F
F
F
F
s
Sign of Work done
• Lowering down an
object at steady speed
– Apply an upward
force F to do work.
– Work done by F is
negative.
– The object loses
gravitational P.E.
F
F
F
F
s
Sign of Work done
• Holding an object.
– Apply an upward
force F.
– Displacement s = 0
– Work done by F is
zero.
– The object neither
gains nor loses energy.
F
s=0
Sign of Work done
• Stretching a spring
unstretched
Sign of Work done
• Stretching a spring
– Apply a force F to
extend the spring.
– Work done by F is
positive.
– The spring gains
elastic P.E.
unstretched
F
s
stretched
Sign of Work done
• Releasing a stretched
spring
– A restoring force F acts
on the spring.
– Work done by F is
negative.
– The spring loses elastic
P.E.
F
stretched
Sign of Work done
• Releasing a stretched
spring
– A force F acts on the
mass.
– Work done by F is
positive.
– The mass gains K.E.
unstretched
F
s
stretched
Work
• Example 7
• Example 8
Forms of Energy
• Kinetic energy (K.E. or Ek )
• Potential energy
– Gravitational
– Elastic
– Electrostatic
• Thermal and internal energy
Forms of Energy
•
•
•
•
Radiant energy
Chemical energy
Nuclear energy
Mass equivalent
• In microscopic scale, molecules possesses
kinetic energy and electrostatic potential
energy only.
Kinetic Energy
1 2
Ek  mv
2
v
m
Kinetic energy
• Prove that the work done F.s is equal to the
1
gain of kinetic energy Ek  mv 2
2
F
v
u=0
m
m
s
Gravitational potential energy
E p  mgh
Gravitational potential energy
• Prove that the work
done F.s is equal to the
gain of gravitational
potential energy
Ep=mgh.
F
s
F
• Note that the motion is
a steady one.
Energy
• Example 9
Elastic potential energy
• F = k.e
• Find the work done to extend a spring for a
length e.
unstretched
F
Elastic potential energy
• F = k.e
• Find the work done to extend a spring for a
length e.
unstretched
F
e
stretched
Elastic potential energy
• F = k.e
• Find the work done to extend a spring for a
length e.
F
F=k.x
e
W   F .dx
0
0
e
x
Elastic potential energy
• F = k.e
• Find the work done to extend a spring for a
length e.
F
F=k.x
e
W   kx.dx
0
0
e
x
Elastic potential energy
• F = k.e
• Find the work done to extend a spring for a
length e.
F
0
F=k.x
e
1 2
W  ke
2
This is also the area
x below the graph.
Elastic potential energy
• Example 10.