* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Static: PowerPoint Notes
Survey
Document related concepts
Transcript
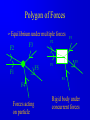
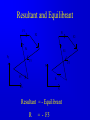
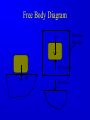
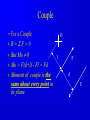
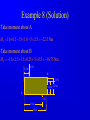
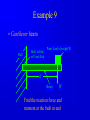
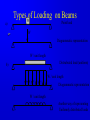
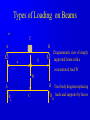
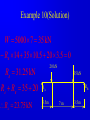
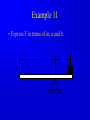
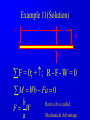
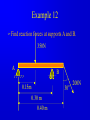
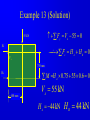
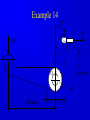
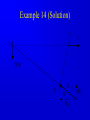
Principle of Engineering ENG2301 Mechanics Section Textbook: A Foundation Course in Statics and Dynamics Addison Wesley Longman 1997 Syllabus Overview A Statics B Dynamics Units force Newton (N) stress Newton per metre squared (N/m2 ) or Pascal, 1 Pa = 1 N/m2 (Pa) pressure Newton per metre squared (N/m2 ) or bar, 1 bar = 1x105 N/m2 (bar) moment, torque, couple Newton . Metre (Nm) Units Most commonly used prefixes micro x 10-6 milli x 10-3 m kilo x 103 k mega x 106 M giga x 109 G * Note Capitals and lower case letters are important Scalars and Vector Two kind of quantities: Scalar Vector Scalar quantities have magnitude but no directional properties can be handled by ordinary algebra, e.g. c= a+b, c= 8 if a=3, b= 5 e.g. time, mass, speed and energy etc. etc.... Vector Associated with directions and magnitude e.g. Force, displacement, acceleration and velocity Can be represented by a straight line with arrowhead and the magnitude is shown by the length l Vector Addition and Subtraction By Triangle or Parallelogram laws Addition V = V1 + V2 V is called the resultant vector V2 V1 V 1 V1 V1 V V2 2 (a) V2 (b) (c) Vector Addition and Subtraction Subtraction V’ = V1 - V2 can be regarded as V’ = V1 + (- V2) - V2 is drawn in the opposite direction V’ is the resultant vector V1 -V2 V1 1 V' 2 -V 2 (a) V1 V' -V 2 (b) (c) Vector Addition and Subtraction Adding more than two vectors V’ = V1 + V2 +V3 +V4 V3 V2 V2 V1 V4 V1+V2 V3 V1 V1+V2+V3 V4 V=V 1+V2+V3 +V4 (a) (b) Resolution of Vectors Any vector can be resolved into components Commonly resolve into two components y perpendicular to each other V = Vx + Vy Vy V Vx = V cos Vy = V sin o Vx 2 2 magnitude V = Vx + Vy ) = tan-1 (Vy /Vx ) x Force and Newton’s First Law First Law - If the resultant force acting on a particle is zero, the particle will remain at rest (if originally at rest), or will move with constant speed in a straight line (if originally in motion). State of Equilibrium - Equilibrium exists when all the forces on a particle are in balance . The velocity of a particle does not change , if the particle is in Equilibrium . Interpretation of First Law A body is in Equilibrium if it moves with constant velocity. A body at rest is a special case of constant velocity i.e. v = 0 = constant. For a body to be in Equilibrium the resultant force (meaning the vector addition of all the forces) acting on the body must be zero. A Force can be defined as 'that which tends to cause a particle to accelerate', assuming that the force is not in Equilibrium with other forces acting on the body. Force A force cannot be seen, only the effect of a force on a body may be seen. Force Units: S.I. Unit ,Newton, (N) or (kN) Force is a vector quantity. It has both magnitude and direction. Force Vectors Polar and Rectangular Coordinates F = Fx Fy ; fy Fx = F.cos ; Fy F.sin ; F = Fx Fy F -1 y tan Fx 2 2 Fy F Fx fx Example 1 Calculate the components in rectangular coordinates of the 600 N force. Solution Fx 600. cos 35 491 N Fy 600. sin 35 344 N Fy 600N 35 Fx Example 2 A force vector has the components 600 kN and 300 kN in the x and y directions respectively, calculate the components in polar coordinates. Solution F 300 600 670.8 kN 2 2 300 tan 26.56 600 1 Resultant Force Parallelogram Method Fy Force F1 F2 R Force F2 Particle Note Resultant R F1 means "equivalent to" Fx Resultant Force Algebraic Method Rx F1, x F2, x F1 cos1 F2 cos 2 F2,y F2 2 F1,x F2,x Ry F1, y F2, y F1 sin 1 F2 sin 2 R Rx R y 2 1 Ry tan Rx 1 F1,y F1 2 Resultant Force Triangle of Forces Method Fy Fy R F2 F1 R F2 F1 Fx Order is not important Fx Example 3 Find the magnitude and direction of the resultant (i.e. in polar coordinates) of the two forces shown in the diagram, a) Using the Parallelogram Method b) Using the Triangle of Forces Method c) Using the algebraic calculation method Solution Example 3 (Solution) 6kN 4kN 15 30 Rx 6 cos 30 4 cos15 1.332 kN Ry 6 sin 30 4 sin 15 4.035 kN R (1.332) 2 (4.035) 2 4.249 kN 4.035 tan 71.73 1.332 1 Or -108.260 from +ve x axis Equilibrium of Concurrent forces F1 Equilibrant E Equilibrant E Force F2 Resultant R Equilibrant E are equal and opposite to Resultant R R Fy E F2 F1 E = -R Fx Conditions for Equilibrium Coplanar: all forces being in the same plane (e.g.only x-y plane, no forces in z direction) Concurrent: all forces acting at the same point (particle) i=n i=n F 0; or F i i=0 i=n x, i i=0 For three forces acting on a particle 0; and Fy, i 0; i=0 Fx,1 Fx,2 Fx,3 0; Fy,1 Fy,2 Fy,3 0; Some Definitions Particle is a material body whose linear dimensions are small enough to be irrelevant Rigid Body is a body that does not deform (change shape) as a result of the forces acting on it . Polygon of Forces Equilibrium under multiple forces F2 F3 F2 F5 F1 F3 F5 F1 F4 F4 Forces acting on particle Rigid body under concurrent forces Resultant and Equilibrant F1 F1 F2 F2 F4 F4 Fy F3 F3 y F5 R Fx x Resultant = - Equilibrant R = - F5 Example 4 The diagram shows three forces acting on a particle . Find the equilibrant by drawing the polygon of forces. 45 kN 84 kN 20 30 50 122 kN Newton’s Third Law The forces of action and reaction between bodies in contact have the same magnitude, but opposite in direction. Hammer BANG! Solid Surface Action and Reaction Free Body Diagram of Hammer Hammer Free Body Boundary Force on Hammer caused by Surface Force on Surface caused by Hammer Solid Surface Free Body diagram of Surface Free Body Diagram Free Body Diagram - used to describe the system of forces acting on a body when considered in isolation R R R mg R Free Body Diagram Free Body W Boundary Wr Reaction W Wa Action System of Particles or Bodies Two or more bodies or particles connected together are referred to as a system of bodies or particles. External Force External forces are all the forces acting on a body defined as a free body or free system of bodies, including the actions due to other bodies and the reactions due to supports. Transmissibility of Force F F F Load and Reaction Loads are forces that are applied to bodies or systems of bodies. Reactions at points supporting bodies are a consequence of the loads applied to a body and the equilibrium of a body. Tensile and Compressive Forces Push on the body which is called a compressive force Pull on a body which is called a tensile force Reaction Action Compressive Force Reaction Action Tensile Force Procedure for drawing a free body diagram Step 1: Imagine the particle to be isolated or cut “free from its surroundings. Draw or sketch its outlined shape. Step 2: Indicate on this sketch all the forces that act on the particle. These forces can be applied surface forces, reaction forces and/or force of attraction. Procedure for drawing a free body diagram Fp Supported pulley Pulling Force Fs Spring F1 Pulling Force F1 Spring Mass Mass Fs mg Procedure for drawing a free body diagram Step 3: The forces that known should be labeled with their proper magnitudes and directions. Letters are used to represent the magnitudes and directions of forces that unknown. Example 5 Ceiling Support Ceiling Support Action Load = 10 N Ring Reaction Force = 10 N Ring Weight = 10 N Weight = 10 N Gravity Load =10 N Free Body boundary Example 6 tow rope Tug No.1 25 Barge 60 Ring . tow rope Tug No.2 Example 6 (Solution) resultant R of the two forces in tow ropes No.1 & No. 2 from the components in the x and y directions: Rx 10 cos 25 30 cos 60 24.06 kN Ry 10 sin 25 30 sin 60 21.75 kN tow rope Tug No.1 25 Barge 60 Ring . tow rope Tug No.2 Example 6 (Solution) R 24.06 21.75 32.43 kN 2 2 21.75 tan 42.1 24.06 1 Equilibrant E = - R E = 32.43 kN 42.1 42.1 R = 32.43 kN Example 6 (Solution) tow rope Tug No.1 25 Barge 60 Ring . Tug No.2 tow rope Resultant R is the sum of the actions of the tow ropes on the barge E=-R Equilibrant E is the reaction of the barge to the ropes Moment and Couple Moment of Force Moment M of the force F about the point O is defined as: M=Fd where d is the perpendicular distance from O to F Moment is directional M o d F Moment and Couple F A r d B M = F.d = F.r.cos Moment = Force x Perpendicular Distance Resultant of A System of Forces arbitrary body subjected to a number of forces F1, F2 & F3. Resultant R = F1 + F2 + F3 Components Rx = F1x + F2x + F3x Ry = F1y + F2y + F3y d3 O F3 d2 An d R F2 d1 F1 Rx F 3y F3 R Ry F2 F1 F 1x F 1y F 3x F 2y F 2x Resultant of A System of Forces d3 O F3 d2 Resultant moment Mo = Sum of Moments Mo = F1 d1 + F2 d2 + F3 d3 Mo = R d d R F2 d1 F1 Rx F 3y F3 R Ry F2 F1 F 1x F 1y F 3x F 2y F 2x Couple For a Couple O R =F = 0 But Mo 0 l Mo = F(d+l) - Fl = Fd Moment of couple is the same about every point in its plane F d F Example 7 Calculate the total (resultant) moment on the body. 300 mm 15 N 30 N 170 mm 30 N A 100 mm 15 N 50 mm Example 7 (Solution) Taking moments about the corner A M 30 0.17 15 0.3 30 0.05 15 0.1 30 0.120 15 0.2 6.6 Nm Note that the forces form two couples or pure moments 3.6 Nm and 3.0 Nm (resultant force =0, moment is the same about any point). Equilibrium of Moments The sum of all the moments is zero when the body is in moment equilibrium. or n M 0 i 1 If i M 1 M 2 ....... 0 the body is in equilibrium the sum of the moments of all the forces on acting on a rigid body is the same for all points on the body. It does not matter at which point on a rigid body you choose for taking moments about Example 8 Calculate the resultant moment and the equilibrant moment. 0.5 m 10 N B 15 N 1.0 m 1.25 m A 5N 2.5 m 3.0 m Example 8 (Solution) Take moment about A M R 10 0.5 15 1.0 5 2.5 22.5 Nm Take moment about B M R 10 2.5 15 0.25 5 0.5 18.75 Nm 0.5 m 10 N B 15 N 1.0 m 1.25 m A 5N 2.5 m 3.0 m Example 8 (Solution) Note that the body is not in vertical and horizontal equilibrium. There is no unique value for the resultant moment. The value depends on where the resultant force acts, ie., depends on the perpendicular distance between the resultant force and the point for taking moment. Therefore, the moments about A and B are different. Example 9 Cantilever Wall beam Built in End or Fixed End Point Load of weight W d Beam W Find the reaction force and moment at the built in end Example 9 (Solution) Taking moment about A M M W .d 0 A M A W .d Fy V W 0 V W W Moment Reaction MA C A d Reaction V Free Body Diagram of Beam B General Equations of Equilibrium of a Plane (Two Dimensional) Rigid Body (Non-concurrent forces) i=n i=n F 0; and F 0; M 0 x, i i=0 n y, i i=0 For complete equilibrium, all 3 equations must be satisfied Fx,1 Fx,2 Fx,3 ... 0; Fy,1 Fy,2 Fy,3 ... 0; M 1 M 2 ....... 0 i 1 i Types of Beam Supports Simply supported beam A beam simply supported on points or knife-edges A side view or elevation of a simply supported beam A diagrammatic view of a simply supported beam Types of Beam Supports Force perpendicular to surface only. Pin Joint supported by a roller Ry Both parallel and Rx perpendicular forces Pin Joint Fixed to the ground Ry Fix Support Two components of force and Rx M Ry a moment Types of Supports and Connections Simply supported beam A beam simply supported on points or knife-edges A side view or elevation of a simply supported beam A diagrammatic view of a simply supported beam Types Wof Loading on Beams Point load a) W Diagrammatic representation W / unit length Distrubuted load (uniform) b) W / unit length Diagrammatic representation W / unit length Another way of representing Uniformly distributed loads Types of Loading on Beams Non-uniformly distributed loads W Types of Loading on Beams C A B W Diagrammatic view of simply supported beam with a b a concentrated load W W B A RA C Free body diagram replacing RB loads and supports by forces Types of Loading on Beams A w N/m a b B Diagrammatic view of simply supported beam with uniformly distributed load w F= w(b-a) (a+b)/2 Free body diagram replacing loads and supports by forces Example 10 Find the reactions at the supports for the beam shown in the diagram. 20 kN 5 kN/m 3.5m 3.5m 7m Example 10(Solution) W 5000 7 35 kN RB 14 35 10.5 20 3.5 0 20 kN RB 31.25 kN RA RB 35 20 RA 23.75 kN 35 kN RB RA 3.5m 7m 3.5m Example 11 Express F F in terms of m, a and b. a b W Example 11(Solution) F b a W R F = 0; + ; R - F - W = 0 M Wb Fa 0 b F W a Ratio a/b is called Mechanical Advantage Example 12 Find reaction forces at supports A and B. 350N A B 0.15m o 30 0.30 m 0.40 m 200N Example 12 (Solution) Consider the sum of vertical forces and horizontal forces are zero, and since RAx = 0 as point B can only take up vertical force. RAx = 200 x sin30o = 100 N RAy + RBy = 350 + 200 cos30o = 350 + 173.2 N = 523.2 N Example 12 (Solution) Taking moment about A, RBy x 0.3 = 350 x 0.15 + 200 cos30o x 0.4 RBy x 0.3 = 121.8 N RBy = 405.9 N Therefore the reaction at point B is 405.9N upward. RAy = 523.2 - 405.9 = 117.3 N Example 12 (Solution) The reaction at point A is 117.3 N upward and 100 N to the left. Resultant at A is: RA = (117.32 + 1002) = 154.1 N 117.3 angle = 49.55o 100 Example 13 Find reaction forces at supports A and B. 55 kN A 750 mm B 600 mm Example 13 (Solution) Fy VA 55 0 55 kN HA Fx H A H B 0 VA 750 mm M H 0.75 55 0.6 0 HB A 600 mm VA 55 kN H A 44 kN H B 44 kN Example 14 20 o T 75 N O 250 mm 100 mm Example 14 (Solution) T 75 N O R Rx Ry Example 14 (Solution) Fy = 0:Ry - 75 = 0 Ry = 75 N Fx = 0:T - Rx = 0T = Rx MO = 0: 75 x 250 - T x 100 x cos 200 =0 Therefore Rx = T = 200 N R = (Rx2 + Ry2) = 214 N = tan-1 (Ry/Rx) = 20o 33’ Example 14 (Solution) Reaction R is that exerted by the frame on the bellcrank, which is equal and opposite to that on the chassis. R R = 214 N 75 N o 20 33' T = 200 N Example 14 (Graphical Solution) Having determined the line of reaction R, a scaled force polygon can be drawn. By measurement, T = 200 N, R = 214 N R = 214 N 75 N o 20 33' T = 200 N