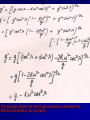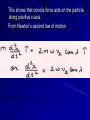* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download EFFECT OF CENTRIFUGAL AND CORIOLIS FORCES DUE TO
Sagnac effect wikipedia , lookup
Mean field particle methods wikipedia , lookup
Particle filter wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Frame of reference wikipedia , lookup
Velocity-addition formula wikipedia , lookup
Elementary particle wikipedia , lookup
Inertial frame of reference wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Relativistic angular momentum wikipedia , lookup
Brownian motion wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Classical mechanics wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Earth's rotation wikipedia , lookup
Mechanics of planar particle motion wikipedia , lookup
Centrifugal force wikipedia , lookup
Jerk (physics) wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Equations of motion wikipedia , lookup
Matter wave wikipedia , lookup
Fictitious force wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Coriolis force wikipedia , lookup
Centripetal force wikipedia , lookup
EFFECT OF CENTRIFUGAL AND CORIOLIS FORCES DUE TO EARTH’S ROTATION ON ‘g’ 1. Effect of centrifugal force The acceleration of a particle in frame of reference S’ rotating with a constant angular velocity ω is given by: ….(1) Here r is position vector of the particle and the other terms have their usual meaning. When a particle is at rest on the surface of earth which rotates with constant angular velocity ω about its polar axis, then: Then, Coriolis acceleration=0 i.e. and Therefore, from equation (1), the acceleration is given by …(2) Acceleration due to gravity at P acts along PO. The components of g are: This acceleration is given by eqn. (2) as where λ is latitude of particle P. This equation shows that centrifugal acceleration decreases the effective acceleration due to gravity. Hence §there is no effect of rotation of earth on the value of acceleration due to gravity at its poles §there is maximum effect of rotation of earth on the value of acceleration due to gravity at its equator. 2. Effect of Coriolis Force Consider a point P at latitude λ on the surface of earth. Let the earth rotate with constant angular velocity ω about its polar axis. ω makes an angle λ with y- axis at point P Imagine a point P’ vertically above P and drop a body of mass ‘m’, then velocity v acquired by it at time ‘t’ is given by: Vx and vy are taken as zero because body has velocity only along negative z-axis. The coriolis force acting on the particle is given by: This shows that coriolis force acts on the particle along positive x-axis. From Newton’s second law of motion Using the relation, v= u+at along negative z-direction. Integration w. r. t. time ‘t’ gives Again integrating w.r.t. t, we get: Hence, due to coriolis force, the particle dropped vertically downwards suffers a deviation along positive x-axis i.e. towards east. The displacement of the particle will be maximum for λ=0 i.e. at the equator. THANX!