Download Lecture 14ba

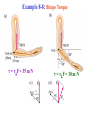
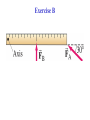
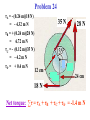
Rotational Dynamics
• Causes of rotational motion!
• Analogies between linear &
rotational motion continue.
• Newton’s 3 Laws are still valid! But,
here we write them using rotational
language and notation.
Translational-Rotational Analogues Continue!
ANALOGUES
Translation
Displacement
x
Velocity
v
Acceleration
a
Force
F
Rotation
θ
ω
α
τ (torque)
Section 8-4: Torque
• Newton’s 1st Law (rotational language version): “A
rotating body will continue to rotate at a
constant angular velocity unless an external
TORQUE acts.”
• Clearly, to understand this, we need to
define the concept of TORQUE.
• Newton’s 2nd Law (rotational language version):
Also needs torque.
• To cause a body to rotate about an axis
requires a FORCE, F. (Cause of angular
acceleration α).
• BUT: The location of the force on the body
and the direction it acts are also important!

Introduce the torque concept.
• Angular acceleration α  F.  From experiment!

• But also α  (the distance from the point of
application of F to the hinge = Lever Arm, r)
Lever Arm
Angular acceleration α  force F, but also  distance
from the point of application of F to the hinge (“Lever Arm”)
FA = FB, but which
gives a greater α ?
Hinge
RA, RB ≡ “Lever Arms” for FA & FB.
α  “Lever Arm”
Section 8-4: Lever Arm
• Lever Arm  r = distance of the axis of
rotation from the “line of action” of force F
• r = Distance which is  to both the axis of
rotation and to an imaginary line drawn along
the direction of the force (“line of action”).
• Find: Angular acceleration
α  (force) (lever arm) = Fr

Define: TORQUE
Lower case
Greek “tau” 
τ  Fr
τ causes α
(Just as in the linear motion case, F causes a)
Door Hinge
Forces at angles are less effective
Torques:

rA  
Due to FA: τA = rAFA
Due to FC : τC = rCFC
Due to FD:
τD = 0
rC is the Lever
Arm for FC
rC
(Since the lever arm is 0)
τC < τA (For FC = FA)
The lever arm for FA is the distance from the knob to the hinge. The
lever arm for FD is zero. The lever arm for FC is as shown.
In general, write τ = rF  These are the



r= r sinθ
τ = rF sinθ
OR, resolve F into
components F & F
same, of course!  
Units of τ:
Nm=mN
τ = rF



F= F sinθ
F = F cosθ
τ = rF sinθ
Torque
• In general, write
τ = rF
• Or, resolving F into components F|| and F:
τ = rF
• Even more generally:
τ = rF sinθ
• Units of torque: Newton-meters (N m)
Example 8-8: Biceps Torque
τ = rF = 35 m N
τ = rF = 30 m N
Exercise B
More than one torque?
• If there is more than one torque:
α  τnet = ∑τ = sum of torques
• Always use the following sign convention!
Counterclockwise rotation  + torque
Clockwise rotation  - torque
Example 8-9
r= rBsin60º -------------->
τB = -rBFBsin60º
2 thin disk-shaped wheels, radii
rA = 30 cm & rB = 50 cm, are
attached to each other on an
axle through the center of each.
Calculate the net torque on this
compound wheel due to the 2
forces shown, each of
magnitude 50 N.
τ = τA + τB
= - 6.7 m N
τA= rAFA
Problem 24
τA = - (0.24 m)(18 N)
= - 4.32 m N
τB = + (0.24 m)(28 N)
= 6.72 m N
τC = - (0.12 m)(35 N)
= - 4.2 m N
τfr = + 0.4 m N
35 N
28 N
12 cm
24 cm
18 N
Net torque: ∑τ = τA + τB + τC + τfr = -1.4 m N
Translational-Rotational Analogues &
Connections Continue!
Displacement
Velocity
Acceleration
Force (Torque)
Mass
Translation
x
v
a
F
m
CONNECTIONS
v = rω
atan= rα
aR = (v2/r) = ω2r
τ = rF
Rotation
θ
ω
α
τ
?