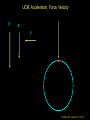* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Physics 207: Lecture 2 Notes
Inertial frame of reference wikipedia , lookup
Classical mechanics wikipedia , lookup
Coriolis force wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Hunting oscillation wikipedia , lookup
Equations of motion wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Fictitious force wikipedia , lookup
Work (physics) wikipedia , lookup
Jerk (physics) wikipedia , lookup
Renormalization group wikipedia , lookup
Rigid body dynamics wikipedia , lookup
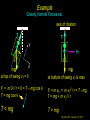
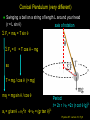
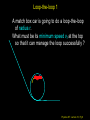
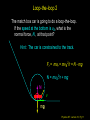
Lecture 10 Goals: Employ Newton’s Laws in 2D problems with circular motion Assignment: HW5, (Chapters 8 & 9, due 3/4, Wednesday) For Tuesday: Finish reading Chapter 8, start Chapter 9. Physics 207: Lecture 10, Pg 1 Uniform Circular Motion For an object moving along a curved trajectory, with non-uniform speed a = ar (radial only) v vT2 |ar |= r ar Perspective is important Physics 207: Lecture 10, Pg 2 Non-uniform Circular Motion For an object moving along a curved trajectory, with non-uniform speed a = ar + at (radial and tangential) at vT2 |ar |= r ar |aT |= d| v | dt Physics 207: Lecture 10, Pg 3 Circular motion Circular motion implies one thing |aradial | =vT2 / r Physics 207: Lecture 10, Pg 4 Key steps Identify forces (i.e., a FBD) Identify axis of rotation Apply conditions (position, velocity, acceleration) Physics 207: Lecture 10, Pg 5 Example The pendulum axis of rotation Consider a person on a swing: When is the tension on the rope largest? And at that point is it : (A) greater than (B) the same as (C) less than the force due to gravity acting on the person? Physics 207: Lecture 10, Pg 6 Example Gravity, Normal Forces etc. axis of rotation T T y vT q x mg at top of swing vT = 0 mg at bottom of swing vT is max Fr = m 02 / r = 0 = T – mg cos q T = mg cos q Fr = m ac = m vT2 / r = T - mg T = mg + m vT2 / r T < mg T > mg Physics 207: Lecture 10, Pg 7 Conical Pendulum (very different) Swinging a ball on a string of length L around your head (r = L sin q) axis of rotation S Fr = mar = T sin q S Fz = 0 = T cos q – mg so T = mg / cos q (> mg) mar = mg sin q / cos q ar = g tan q = vT2/r vT = (gr tan q)½ Period: t = 2p r / vT =2p (r cot q /g)½ Physics 207: Lecture 10, Pg 8 Loop-the-loop 1 A match box car is going to do a loop-the-loop of radius r. What must be its minimum speed vt at the top so that it can manage the loop successfully ? Physics 207: Lecture 10, Pg 9 Loop-the-loop 1 To navigate the top of the circle its tangential velocity vT must be such that its centripetal acceleration at least equals the force due to gravity. At this point N, the normal force, goes to zero (just touching). Fr = mar = mg = mvT2/r vT vT = (gr)1/2 mg Physics 207: Lecture 10, Pg 10 Loop-the-loop 2 The match box car is going to do a loop-the-loop. If the speed at the bottom is vB, what is the normal force, N, at that point? Hint: The car is constrained to the track. Fr = mar = mvB2/r = N - mg N = mvB2/r + mg N v mg Physics 207: Lecture 10, Pg 11 Loop-the-loop 3 Once again the car is going to execute a loop-the-loop. What must be its minimum speed at the bottom so that it can make the loop successfully? This is a difficult problem to solve using just forces. We will skip it now and revisit it using energy considerations later on… Physics 207: Lecture 10, Pg 12 Example, Circular Motion Forces with Friction (recall mar = m |vT | 2 / r Ff ≤ ms N ) How fast can the race car go? (How fast can it round a corner with this radius of curvature?) mcar= 1600 kg mS = 0.5 for tire/road r = 80 m g = 10 m/s2 r Physics 207: Lecture 10, Pg 14 Example Only one force is in the horizontal direction: static friction x-dir: Fr = mar = -m |vT y-dir: ma = 0 = N – mg |2/ y r = Fs = -ms N (at maximum) N = mg vT = (ms m g r / m )1/2 vT = (ms g r )1/2 = (0.5 x 10 x 80)1/2 vT = 20 m/s N Fs mg mcar= 1600 kg mS = 0.5 for tire/road r = 80 m g = 10 m/s2 Physics 207: Lecture 10, Pg 15 x Another Example A horizontal disk is initially at rest and very slowly undergoes constant angular acceleration. A 2 kg puck is located a point 0.5 m away from the axis. At what angular velocity does it slip (assuming aT << ar at that time) if ms=0.8 ? Only one force is in the horizontal direction: static friction y x-dir: Fr = mar = -m |vT | 2 / r = Fs = -ms N (at w) y-dir: ma = 0 = N – mg N = mg vT = (ms m g r / m )1/2 vT = (ms g r )1/2 = (0.8 x 10 x 0.5)1/2 vT = 2 m/s w = vT / r = 4 rad/s N Fs mg mpuck= 2 kg mS = 0.8 r = 0.5 m g = 10 m/s2 Physics 207: Lecture 10, Pg 16 x UCM: Acceleration, Force, Velocity F a v Physics 207: Lecture 10, Pg 17 Zero Gravity Ride A rider in a “0 gravity ride” finds herself stuck with her back to the wall. Which diagram correctly shows the forces acting on her? Physics 207: Lecture 10, Pg 18 Banked Curves In the previous car scenario, we drew the following free body diagram for a race car going around a curve on a flat track. n Ff mg What differs on a banked curve? Physics 207: Lecture 10, Pg 19 Banked Curves Free Body Diagram for a banked curve. Use rotated x-y coordinates Resolve into components parallel and perpendicular to bank N mar Ff q y x mg For very small banking angles, one can approximate that Ff is parallel to mar. This is equivalent to the small angle approximation sin q = tan q, but very effective at pushing the car toward the center of the curve!! Physics 207: Lecture 10, Pg 20 Banked Curves, Testing your understanding Free Body Diagram for a banked curve. Use rotated x-y coordinates Resolve into components parallel and perpendicular to bank N mar Ff q x y mg At this moment you press the accelerator and, because of the frictional force (forward) by the tires on the road you accelerate in that direction. How does the radial acceleration change? Physics 207: Lecture 10, Pg 21 Locomotion: how fast can a biped walk? Physics 207: Lecture 10, Pg 22 How fast can a biped walk? What about weight? (a) A heavier person of equal height and proportions can walk faster than a lighter person (b) A lighter person of equal height and proportions can walk faster than a heavier person (c) To first order, size doesn’t matter Physics 207: Lecture 10, Pg 23 How fast can a biped walk? What about height? (a) A taller person of equal weight and proportions can walk faster than a shorter person (b) A shorter person of equal weight and proportions can walk faster than a taller person (c) To first order, height doesn’t matter Physics 207: Lecture 10, Pg 24 How fast can a biped walk? What can we say about the walker’s acceleration if there is UCM (a smooth walker) ? Acceleration is radial ! So where does it, ar, come from? (i.e., what external forces are on the walker?) 1. Weight of walker, downwards 2. Friction with the ground, sideways Physics 207: Lecture 10, Pg 25 How fast can a biped walk? What can we say about the walker’s acceleration if there is UCM (a smooth walker) ? Acceleration is radial ! So where does it, ar, come from? (i.e., what external forces are on the walker?) 1. Weight of walker, downwards 2. Friction with the ground, sideways Physics 207: Lecture 10, Pg 26 How fast can a biped walk? What can we say about the walker’s acceleration if there is UCM (a smooth walker) ? Acceleration is radial ! So where does it, ar, come from? (i.e., what external forces are on the walker?) 1. Weight of walker, downwards 2. Friction with the ground, sideways (most likely from back foot, no tension along the red line) 3. Need a normal force as well Physics 207: Lecture 10, Pg 27 How fast can a biped walk? What can we say about the walker’s acceleration if there is UCM (a smooth walker) ? Acceleration is radial ! So where does it, ar, come from? (i.e., what external forces are on the walker?) 1. Weight of walker, downwards 2. Friction with the ground, sideways (Notice the new direction) Physics 207: Lecture 10, Pg 28 How fast can a biped walk? Given a model then what does the physics say? Choose a position with the simplest constraints. If his radial acceleration is greater than g then he is “in orbit” Fr = m ar = m v2 / r < mg Otherwise you will lose contact! ar = v2 / r vmax = (gr)½ vmax ~ 3 m/s ! (And it pays to be tall and live on Jupiter) Physics 207: Lecture 10, Pg 29 Orbiting satellites vT = (gr)½ Physics 207: Lecture 10, Pg 30 Geostationary orbit Physics 207: Lecture 10, Pg 31 Geostationary orbit The radius of the Earth is ~6000 km but at 36000 km you are ~42000 km from the center of the earth. Fgravity is proportional to r-2 and so little g is now ~10 m/s2 / 50 vT = (0.20 * 42000000)½ m/s = 3000 m/s At 3000 m/s, period T = 2p r / vT = 2p 42000000 / 3000 sec = = 90000 sec = 90000 s/ 3600 s/hr = 24 hrs Orbit affected by the moon and also the Earth’s mass is inhomogeneous (not perfectly geostationary) Great for communication satellites (1st pointed out by Arthur C. Clarke) Physics 207: Lecture 10, Pg 32