Download Review - Weebly

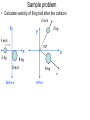
Law of Conservation of Momentum
Law of Conservation of Momentum
• If the resultant external force on a
system is zero, then the vector sum
of the momentums of the objects will
remain constant.
•
Sρbefore = Sρafter
Sample problem
• A 75-kg man sits in the back of a 120-kg canoe
that is at rest in a still pond. If the man begins to
move forward in the canoe at 0.50 m/s relative to
the shore, what happens to the canoe?
External versus internal forces
• External forces: forces coming from
outside the system of particles whose
momentum is being considered.
– External forces change the momentum of the
system.
• Internal forces: forces arising from
interaction of particles within a system.
– Internal forces cannot change momentum of
the system.
Explosions
• When an object separates suddenly, as in
an explosion, all forces are internal.
• Momentum is therefore conserved in an
explosion.
• There is also an increase in kinetic energy
in an explosion. This comes from a potential
energy decrease due to chemical
combustion.
Recoil
• Guns and cannons “recoil” when fired.
• This means the gun or cannon must move
backward as it propels the projectile
forward.
• The recoil is the result of action-reaction
force pairs, and is entirely due to internal
forces. As the gases from the gunpowder
explosion expand, they push the projectile
forwards and the gun or cannon backwards.
Sample problem
• Suppose a 5.0-kg projectile launcher
shoots a 209 gram projectile at 350 m/s.
What is the recoil velocity of the
projectile launcher?
Sample Problem
• A firecracker is placed in a pumpkin which explodes into
exactly two pieces. The first piece has a mass of 2.2 kg
and flies due east at 26 m/s. The second chunk heads
due west at 34 m/s. What was the initial mass of the
pumpkin?
Collisions
• When two moving objects make contact
with each other, they undergo a collision.
• Conservation of momentum is used to
analyze all collisions.
• Newton’s Third Law is also useful. It tells
us that the force exerted by body A on
body B in a collision is equal and opposite to
the force exerted on body B by body A.
Collision Types
• Elastic collisions
– Also called “hard” collisions
– No deformation occurs, no kinetic energy lost
• Inelastic collisions
– Deformation occurs, kinetic energy is lost
• Perfectly Inelastic (stick together)
– Objects stick together and become one object
– Deformation occurs, kinetic energy is lost
(Perfectly) Inelastic Collisions
• Simplest type of collisions.
• After the collision, there is only one
velocity, since there is only one
object.
• Kinetic energy is lost.
• Perfectly inelastic collisions are the
reverse of explosions in which kinetic
energy is gained!
Sample Problem
• An 80-kg roller
skating grandma
collides inelastically
with a 40-kg kid.
What is their
velocity after the
collision?
• How much kinetic
energy is lost?
Sample Problem
• A fish moving at 2 m/s
swallows a stationary
fish which is 1/3 its
mass. What is the
velocity of the big fish
after dinner?
Sample problem
• A car with a mass of 950 kg and a speed of 16 m/s to the
east approaches an intersection. A 1300-kg minivan traveling
north at 21 m/s approaches the same intersection. The
vehicles collide and stick together. What is the resulting
velocity of the vehicles after the collision?
Elastic Collision
• In elastic collisions, there is no
deformation of colliding objects, and no
change in kinetic energy of the system.
•
•
Spb = Spa (momentum conservation)
SKb = SKa (kinetic energy conservation)
A couple tips
• Always start with conservation of
momentum and only move on to
conservation of kinetic energy if you
don’t have enough information to
solve the conservation of momentum
equations
A couple tips
• When objects stick together, the
collision must be inelastic, but if
objects bounce off each other, it can
be elastic OR inelastic. SO only use
conservation of kinetic energy if the
problem says that it is an elastic
collision OR if the problem asks you if
the collision is elastic and you use it
to test and see if kinetic energy is
conserved
Sample Problem
• A 500-g cart moving at 2.0 m/s on an air track strikes
a 1,000-g cart at rest in an elastic collision. What are
the resulting velocities of the two carts?
Example
• Two carts of equal mass move towards each other
with identical speeds of 0.3 m/s. After colliding,
the carts bounce off each other, each regaining
0.30 m/s of speed, but now moving in the opposite
direction. Is this an elastic collision?
2D-Collisions
• Momentum in the x-direction is conserved.
– SPx (before) = SPx (after)
• Momentum in the y-direction is conserved.
– SPy (before) = SPy (after)
• Treat x and y coordinates independently.
– Ignore x when calculating y
– Ignore y when calculating x
• Let’s look at a simulation:
– http://surendranath.tripod.com/Applets.html
Sample problem
• Calculate velocity of 8-kg ball after the collision.
2 m/s
y
2 kg
y
3 m/s
50o
x
2 kg
x
8 kg
0 m/s
Before
8 kg
After
v
Motion of the Center of Mass
• The center of mass of a system of objects obeys
Newton’s second law.
• To find the center of mass
– If the objects are of equal mass, the center of mass is
directly between them
– If the objects are not of equal mass, set up a proportion
(the center of mass will be closer to the heavier mass)
Example
• A toy rocket is in projectile motion, so that it is on
track to land 30 m from its launch point. While in
the air, the rocket explodes into two identical
pieces, one of which lands 35 m from its launch
point. Where does the first piece land?
• 25 m from its launch point. Since the only
external force acting on the rocket is gravity, the
center of mass must stay in projectile motion, and
must land 30 m from the launch point. The two
pieces are of equal mass so if one is 5 m beyond
the center of mass landing point, one must be 4 m
short of that point.
• C:\Users\rsm13030\AppData\Local\
Temp\phet-collision-lab\collisionlab_en.html
Ballistics Pendulum
• A ballistics pendulum was used in
munitions factory to test the velocity
of the bullets manufactured. A bullet
is fired into a block of wood hanging
on a string. The height to which the
pendulum swings is measured and
from this the initial velocity of the
bullet can be measured.
Example
• A bullet with mass of 0.05 kg is fired
into a ballistics pendulum with mass 3
kg. It swings to a height of 0.32 m.
What is the velocity of the bullet?