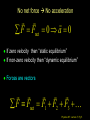Download Physics 207: Lecture 2 Notes

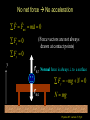
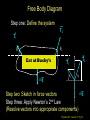
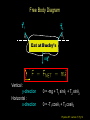
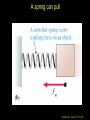
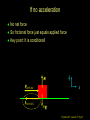
Lecture 7
 Goals:
 Identify the types of forces
 Use a Free Body Diagram to solve 1D and 2D
problems with forces in equilibrium and non-equilibrium
(i.e., acceleration) using Newton’ 1st and 2nd laws.
 Distinguish static and kinetic coefficients of friction
1st Exam Thursday, Oct. 6 from
7:15-8:45 PM Chapters 1-7(light)
Physics 207: Lecture 7, Pg 1
Chaps. 5, 6 & 7
What causes motion?
(actually changes in motion)
What kinds of forces are there ?
How are forces & changes in motion related?
Physics 207: Lecture 7, Pg 2
Newton’s First Law and IRFs
An object subject to no external forces moves with constant
velocity if viewed from an inertial reference frame (IRF).
If no net force acting on an object, there is no
acceleration.

The above statement can be used to define inertial
reference frames.
Physics 207: Lecture 7, Pg 3
IRFs
 An IRF is a reference frame that is not
accelerating (or rotating) with respect to the “fixed
stars”.
 If one IRF exists, infinitely many exist since they
are related by any arbitrary constant velocity vector!
 In many cases (i.e., Chapters 5, 6 & 7) the surface
of the Earth may be viewed as an IRF
Physics 207: Lecture 7, Pg 4
No net force  No acceleration
 

 F  Fnet  0  a  0
If zero velocity then “static equilibrium”
 If non-zero velocity then “dynamic equilibrium”


Forces are vectors
 
  
 F  Fnet  F1  F2  F3  
Physics 207: Lecture 7, Pg 5
Newton’s Second Law
The acceleration of an object is directly proportional to the
net force acting upon it.
The constant of proportionality is the mass.

This is a vector expression: Fx, Fy, Fz

Units
The metric unit of force is kg m/s2 = Newtons (N)
The English unit of force is Pounds (lb)
Physics 207: Lecture 7, Pg 6
Example Non-contact Forces
All objects having mass exhibit a mutually attractive force
(i.e., gravity) that is distance dependent
At the Earth’s surface this variation is small so little “g” (the
associated acceleration) is typically set to 9.80 or 10. m/s2
FB,G
Physics 207: Lecture 7, Pg 7
Contact (e.g., “normal”) Forces
Certain forces act to keep an object in place.
These have what ever force needed to balance all
others (until a breaking point).
Here: A contact force from the table opposes gravity,
Normal force is perpendicular to the surface.
FB,T
Physics 207: Lecture 7, Pg 8
No net force  No acceleration
 

 F  Fnet  ma  0
 Fx  0
 Fy  0
y
(Force vectors are not always
drawn at contact points)
FB,T Normal force is always  to a surface
 Fy  mg  N  0
FB,G
N  mg
Physics 207: Lecture 7, Pg 9
High Tension
A crane is lowering a load of bricks on a pallet. A
plot of the position vs. time is
 There are no frictional forces
 Compare the tension in the
crane’s wire (T) at the point
it contacts the pallet to the
weight (W) of the load (bricks
+ pallet)
Time
Height

A: T > W B: T = W C: T< W D: don’t know
Physics 207: Lecture 7, Pg 10
Important notes

Many contact forces are conditional and, more
importantly, they are not necessarily constant

We have general idea of forces from everyday life.

In physics the definition must be precise.
A force is an action which causes a body to
accelerate.
(Newton’s Second Law)

On a microscopic level, all forces are non-contact
Physics 207: Lecture 7, Pg 11
Analyzing Forces: Free Body Diagram
A heavy sign is hung between two poles by a rope at
each corner extending to the poles.
Eat at Bucky’s
A hanging sign is an example of static equilibrium
(depends on observer)
What are the forces on the sign and how are they
related if the sign is stationary (or moving with
constant velocity) in an inertial reference frame ?
Physics 207: Lecture 7, Pg 12
Free Body Diagram
Step one: Define the system
T2
T1
q2
q1
Eat at Bucky’s
mg
T2
T1
q1
q2
mg
Step two: Sketch in force vectors
Step three: Apply Newton’s 2nd Law
(Resolve vectors into appropriate components)
Physics 207: Lecture 7, Pg 13
Free Body Diagram
T1
T2
q2
q1
Eat at Bucky’s
mg
Vertical :
y-direction
Horizontal :
x-direction
0 = -mg + T1 sinq1 + T2 sinq2
0 = -T1 cosq1 + T2 cosq2
Physics 207: Lecture 7, Pg 14
Scale Problem

You are given a 5.0 kg mass and you hang it
directly on a fish scale and it reads 50 N (g is
10 m/s2).
50 N
5.0 kg




Now you use this mass in a second
experiment in which the 5.0 kg mass hangs
from a massless string passing over a
massless, frictionless pulley and is anchored
to the floor. The pulley is attached to the fish
scale.
What does the string do?
What does the pulley do?
What does the scale now read?
?
5.0 kg
Physics 207: Lecture 7, Pg 15
Pushing and Pulling Forces


String or ropes are examples of
things that can pull
You arm is an example of an object
that can push or push
Physics 207: Lecture 7, Pg 16
Examples of Contact Forces:
A spring can push
Physics 207: Lecture 7, Pg 17
A spring can pull
Physics 207: Lecture 7, Pg 18
Ropes provide tension (a pull)
In physics we often use a “massless” rope with opposing
tensions of equal magnitude
Physics 207: Lecture 7, Pg 19
Moving forces around
Massless strings: Translate forces and reverse their
direction but do not change their magnitude
(we really need Newton’s 3rd of action/reaction to justify)

string
T1

-T1
Massless, frictionless pulleys: Reorient force direction but
do not change their magnitude
T2
T1
-T1
| T1 | = | -T1 | = | T2 | = | T2 |
-T2
Physics 207: Lecture 7, Pg 20
Scale Problem

You are given a 5.0 kg mass and you hang it
directly on a fish scale and it reads 50 N (g is
10 m/s2).
50 N
5.0 kg


Now you use this mass in a second
experiment in which the 5.0 kg mass hangs
from a massless string passing over a
massless, frictionless pulley and is anchored
to the floor. The pulley is attached to the fish
scale.
What force does the fish scale now read?
?
5.0 kg
Physics 207: Lecture 7, Pg 21
What will the scale read?
A 25 N
B 50 N
C 75 N
D 100 N
E something else
Physics 207: Lecture 7, Pg 22
Scale Problem


Step 1: Identify the system(s).
In this case it is probably best to treat each
object as a distinct element and draw three
force body diagrams.
 One around the scale
 One around the massless pulley (even
though massless we can treat is as an
“object”)
 One around the hanging mass
Step 2: Draw the three FBGs. (Because this
is a now a one-dimensional problem we
need only consider forces in the y-direction.)
?
5.0 kg
Physics 207: Lecture 7, Pg 23
Scale Problem
3:
T”
T’
1:
2:
T
?
W

-T ’
S Fy = 0 in all cases
1.0 kg
-T
-T
?
-mg
1: 0 = -2T + T ’
2: 0 = T – mg  T = mg
3: 0 = T” – W – T ’ (not useful here)
 Substituting 2 into 1 yields T ’ = 2mg = 100 N
(We start with 50 N but end with 100 N)
5.0 kg
Physics 207: Lecture 7, Pg 24
Home Exercise, Newton’s 2nd Law
A woman is straining to lift a large crate, without success. It
is too heavy. We denote the forces on the crate as follows:
P is the upward force being exerted on the crate by the person
C is the contact or normal force on the crate by the floor, and
W is the weight (force of the earth on the crate).
Which of following relationships between these forces is
true, while the person is trying unsuccessfully to lift the
crate? (Note: force up is positive & down is negative)
A.
B.
C.
D.
P+C<W
P+C>W
P=C
P+C=W
Physics 207: Lecture 7, Pg 25
A “special” contact force: Friction


What does it do?
 It opposes motion (velocity, actual or that which
would occur if friction were absent!)
How do we characterize this in terms we have learned?
 Friction results in a force in a direction opposite to
the direction of motion (actual or, if static, then
“inferred”)!
j
N
FAPPLIED
ma
fFRICTION
i
mg
Physics 207: Lecture 7, Pg 26
If no acceleration



No net force
So frictional force just equals applied force
Key point: It is conditional!
N
FAPPLIED
fFRICTION
j
i
mg
Physics 207: Lecture 7, Pg 27
Friction...

Friction is caused by the “microscopic” interactions between
the two surfaces:
Physics 207: Lecture 7, Pg 28
Friction: Static friction
Static equilibrium: A block with a horizontal force F applied,
S Fx = 0 = -F + fs
 fs = F
FBD
S Fy = 0 = - N + mg  N = mg
As F increases so does fs
N
F
m
fs
1
mg
Physics 207: Lecture 7, Pg 29
Recap
 Assignment:
Soon….HW4 (Chapters 6 & 7, due 10/4)
 Read through first half of Chapter 7
Physics 207: Lecture 7, Pg 30