* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Slide 1
Negative mass wikipedia , lookup
Lunar theory wikipedia , lookup
Introduction to general relativity wikipedia , lookup
Equivalence principle wikipedia , lookup
Coriolis force wikipedia , lookup
Lorentz force wikipedia , lookup
N-body problem wikipedia , lookup
Fictitious force wikipedia , lookup
Schiehallion experiment wikipedia , lookup
Roche limit wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Centrifugal force wikipedia , lookup
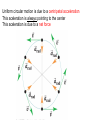
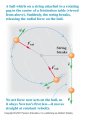
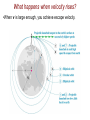
CHAPTER 6 CIRCULAR MOTION AND GRAVITATION Goals for Chapter 6 • To understand the dynamics of circular motion. • To study the unique application of circular motion as it applies to Newton’s Law of Gravitation. • To study the motion of objects in orbit as a special application of Newton’s Law of Gravitation. Uniform circular motion is due to a centripetal acceleration This aceleration is always pointing to the center This aceleration is due to a net force • Period = the time for one revolution 1) Circular motion in horizontal plane: - flat curve - banked curve - rotating object 2) Circular motion in vertical plane Rounding a flat curve • The centripetal force coming only from tire friction. Rounding a banked curve • The centripetal force comes from friction and a component of force from the car’s mass Dynamics of a Ferris Wheel The "Giant Swing" at a county fair consists of a vertical central shaft with a number of horizontal arms attached at its upper end. Each arm supports a seat suspended from a 5 m long cable, the upper end of which is fastened to the arm at a point 3m from the central shaft. Find the time of one revolution of the swing if the cable supporting the seat makes an angle of 300 with the vertical. GRAVITATION Spherically symmetric objects interact gravitationally as though all the mass of each were concentrated at its center Cavendish Balance •The slight attraction of the masses causes a nearly imperceptible rotation of the string supporting the masses connected to the mirror. •Use of the laser allows a point many meters away to move through measurable distances as the angle allows the initial and final positions to diverge. Newton’s Law of Gravitation • Always attractive. • Directly proportional to the masses involved. • Inversely proportional to the square of the separation between the masses. • Masses must be large to bring Fg to a size even close to humanly perceptible forces. A diagram of gravitational force G = 6.674x10-11 N.m2/kg2 Each mass is 2 kg Find the magnitude of the net gravitational force on each mass and its direction Each mass in the figure below is 3 kg. Find the force (magnitude and direction) on each mass in the figure . WEIGHT Gravitational force falls off quickly • If either m1 or m2 are small, the force decreases quickly enough for humans to notice. • In January 2005 the Huygens probe landed on Saturn's moon Titan, the only satellite in the solar system having a thick atmosphere. Titan's diameter is 5150 km, and its mass is 1.35×1023 kg, The probe weighed 3120 N on earth. What did it weigh on the surface of Titan? Satellite Motion What happens when velocity rises? •When v is large enough, you achieve escape velocity. The principle governing the motion of the satellite is Newton’s second law; the force is F, and the acceleration is v2/r, so the equation Fnet = ma becomes GmmE/r 2 = mv 2/r v = GmE/r T= 2πr/v = (2πr3/2)/ GmE Larger orbits correspond to slower speeds and longer periods. A 320 kg satellite experiences a gravitational force of 800 N. What is the radius of the of the satellite’s orbit? What is its altitude? F = GmEmS/r 2 r 2 = GmEmS/ F r 2 = (6.67 x 10 -11 N.m2/kg2) (5.98 x 10 24 kg) (320 kg ) / 800 N r 2 = 1.595 x 1014 m2 r = 1.26 x 107 m Altitude = 1.26 x 107 m – radius of the Earth Altitude = 1.26 x 107 m – 0.637 x 107 = 0.623 x 107 m We want to place a satellite into circular orbit 300km above the earth surface. What speed, period and radial acceleration it must have?