Download Document

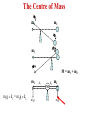
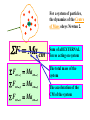
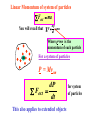
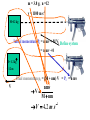
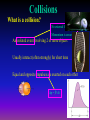
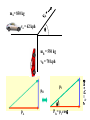
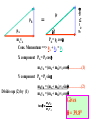
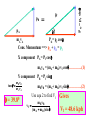
Summary Lecture 8
Systems of Particles
9.2
Centre of mass
9.3
Tomorrow 12 – 2 pm
Newton 2 for system of particles
Conservation of momentum Week
PPP “ExtEnsion”
March 20 – 24
lecture.
20-minute
test
9.8-11
Collisions
on material in
9.12
Rocket propulsion
Room
211 podium
lectures
1-7
level
Turn up any time
Problems:Chap. 9: 1, 6, 10 , 15, 20,
9.4-7
27, 40, 71, 73, 78
So far we have considered the motion of
POINT PARTICLES
FINITE OBJECTS
can move as a whole
(translational motion)
and also
rotate about the “Centre of Mass”
The “Centre of Mass” is that point where if
we apply a force, the object will not rotate.
What happens depends on where we apply the force
The Centre of Mass
Lizzie Borden took an axe
The
motion of the Centre of
And gave her mother forty whacks.
Mass
isshe
a simple
And
when
saw whatparabola.
she had done,
She gave her father forty-one
(just like a point particle)
The motion of the entire
object is complicated.
This motion resolves to
•motion of the CM
•motion of points
around the CM
The Centre of Mass
m1
m2
m1
m2
M = m1 + m 2
m1
m1g x d1 = m2g x d2
m1g
d1
CM
M
d2
m2
m2g
Centre of Mass (1D)
M = m 1 + m2
M
m1
0
x1
m2
x2
xcm
M xcm = m1 x1 + m2 x2
xcm
moment of M = moment of individual masses
m1x1  m 2x 2

M
In general
xcm
1
  m i xi
M
Centre of Mass (3D)
For a collection of masses in 3D
cm
r1
r2 r 3
r cm
1
  mi r i
M
Centre of Mass (3D)
For a collection of masses in 3D
rcm = ixcm +jycm
cm
r cm
1
  mi r i
M
1
xcm 
mi x i

M
1
ycm 
mi yi

M
So in a solid body we can
find the CM by finding
xcm and ycm
y
2
1
xcm   mi xi
M
1
1
xcm  ( 3x0  8x1  4x2)
15
15 kg
4 kg
3 kg
Xcm = 16/15 = 1.07 m
y cm
1
 mi y i

M
y cm 
rCM
1.33
r cm
1
  mi r i
M
8 kg
0
1
( 3x0  8x2  4x1)
15
ycm = 20/15 = 1.33 m
1
1.07
2
x
Finding the Centre of Mass
For solid bodies the sum: rcm  1
r m

M
becomes an integral:
1
rcm   r dm
M
For odd shaped objects this probably needs to
be determined experimentally
For symmetric objects this can often be calculated
1. Look for a symmetry axis
2. Then carry out the integral to find the
position of xcm along the axis.
Solid cone
h
R
Symmetry line
r
xcm
x
1
 x dm
M
R 2 h 3
xcm  2 0 x dx
hM
R 2 h4
xcm 
x
dx
dm = r2 dx
but r = (R/h)x
dm =  (R/h)2x2 dx
Mass of cone M = 1/3 R2 h
xcm 
h2 M 4
R 2 h h
xcm 
M 4
xcm 
3M h
M 4
xcm = ¾ h
cm
F  Ma cm
 Fext  z
 Macm  z
 Fext  y
 Macm  y
 Fext  x
 Macm  x
For a system of particles,
the dynamics of the Centre
of Mass obeys Newton 2.
Sum of all EXTERNAL
forces acting on system
The total mass of the
system
The acceleration of the
CM of the system
cm
CM
F  Ma cm
 Fext  z
 Macm  z
 Fext  y
 Macm  y
 Fext  x
 Macm  x
This also applies to a solid
For awhere
systemthe
of individual
particles,
body,
the dynamics
of the Centre
particles
are rigidly
of Mass obeys
2.
connected.
TheNewton
dynamics
of the Centre of Mass obeys
Newton 2
Linear Momentum of system of particles
 Fext  ma
You will recall that  F 
dp
 ma
dt
Where p=mv is the
momentum of each particle
cm
For a system of particles
P == Mv
p cm
 Fext 
dP
dt
This also applies to extended objects
for system
of particles
Conservation of Linear Momentum
 Fext
If Fext = 0
dP
0
dt
dP

dt
NO EXTERNAL
forces act on the
system
P is a constant
That is: Px, Py and Pz remain constant
if Fext-x, Fext-y and Fext-z are zero
In an isolated system, momentum is conserved.
Exploding rocket
C of M
Why?
No external horizontal forces
so horiz momentum unchanged
m = 3.8 g, n =12
v = 1100 m s-1
M=12 kg
Initial momentum Pi = n mv + M Vi Define system
= n mv + 0
M= 12 kg
+ 12 m
Final momentum pf = (M + nm) V = Pi = n mv
V
nmv
V
M  nm
 V  4.2 m s
1
m = 3.8 g, n =12
v = 1100 m s-1
KE initial
M=12 kg
½ n mv2
½ x 12 x 0.0038 x (1100)2
Initial momentum Pi = n mv + M Vi
27588 J
= n mv + 0
KE final
M= 12 kg
½ (M + 12m)V2
+ 12 m
V
2
½
x
(12.0456)
x
4.2
Final momentum pf = (M + nm) V = Pi = n mv
163 J
nmv
V
M  nm
 V  4.2 m s
1
Collisions
What is a collision?
No external forces
Momentum is conserved
An isolated event involving 2 or more objects
Usually interact (often strongly) for short time
Equal and opposite impulses are exerted on each other
p = F dt
Collisions
Elastic collisions
Energy and momentum are conserved
But Energy
is always
conserved???
Inelastic collisions
Only momentum is conserved
In 1 dimension
Elastic Collision 1D
Before
After
m1
m2
v1i
v2i = 0
m1
m2
v1f
v2f
We want to find V1f and V2f
Mom. Cons.

m1v1i = m1v1f + m2v2f………………(1)
m2v2f = m1(v1i- v1f)…………………(2)
Energy Cons
½ m1v1f2 + ½ m2v2f2 = ½ m1v1i2

½ m2v2f2 = ½ m1(v1i2 - v1f2)
Mult. by 2 and factorise

m2v2f2 = m1(v1i- v1f) (v1i+ v1f) ……(3)
Divide equ. (3) by (2)  v2f = v1i + v1f …………….…(4)
V1i is usually given, so to find v2f we need to find an
expression for v1f. Get this from equ. (1).
m1v1f = m1v1i - m2v2f  v1 f  m1v1i  m2 v 2 f  v1i  m2 v 2 f
m1
m1
Substitute this form of v1f into equ 4  v2f = v1i + v1i – m2/m1 v2f
2m1
v2 f  (
)v1 i
m1  m 2
m1  m2
v1 f  (
)v1i
m1  m2
 v2f(1 + m2/m1) = 2v1i
m1  m2
2m1
)v1i
v2 f  (
)v1 i v1 f  (
m1  m2
m1  m 2
If m1>> m2
v2f
2v1i
v1f
v1i
If m2>>m1
v2f
0
v1f
-v1i
If m1= m2
v2f
v1i
v1f
0
Motion of the C of M
m1
vcm
v1i
m2
v2i =0
CM
What is Vcm?
Mom of CM = mom of m1 + mom of m2
(m1 + m2 ) Vcm = m1v1i + m2v2i
Vcm 
m1
v1i
m1  m 2
Motion of the C of M
m1
vcm
v1i
m2
v2i =0
CM
Let’s observe the
elastic collision
from the view
point of the centre
of mass
In 1 dimension
m1
vcm
v1i
m2
v2i =0
CM
What is Vcm?
Mom of CM = mom of m1 + mom of m2
(m1 + m2 ) Vcm = m1v1i + m2v2i
Vcm 
m1
v1i
m1  m 2
m1
v1i
m2
vcm
CM
v2i
Let’s observe the
elastic collision
from the view
point of the centre
of mass
Collisions in 2 dimensions
Elastic
billiard balls
comets
a-particle scattering
Elastic collisions in 2-D
Momentum is conserved
Impact
parameter
Consider x-components
m1v1i= m1v1f cos 1 + m2v2f cos 2
Consider y-components
0= -m1v1f sin 1 + m2v2f sin 2
Since elastic collision
energy is conserved
m1v1i
2
1
before
1
1
1
2
2
m1 v 1i  m1 v 1f  m 2 v 22f
2
2
2
7 variables!
after
3 equations
Collisions in 2 dimensions
Inelastic
Almost any real collision!
an example
Automobile collision
mA= 830 kg
va = 62 kph

mB = 550 kg
pB
pA
pf

Pfx= pf cos
Pfy= pf sin
vB = 78 kph
=
Pfy= pf sin
pB
pf

mAvA
Pfx= pf cos
Cons. Momentum ==> pA + pB = pf
pA
X component PA = Pf cos
mAvA = (mA+ mB) vf cos………….(1)
Y component PB = Pf sin
Divide equ (2) by (1)
mBvB = (mA+ mB) vf sin………….(2)
____________________
mAvA = (mA+ mB) vf cos
m v
tan  B B
m Av A
Gives
 = 39.80
=

mAvA
Pfx= pf cos
Cons. Momentum ==> pA + pB = pf
pA
Pfy= pf sin
pB
pf
X component PA = Pf cos
mAvA = (mA+ mB) vf cos………….(1)
Y component PB = Pf sin
tan 
=
mBvB
m Av A
39.80
mBvB = (mA+ mB) vf sin………….(2)
Use equ 2 to find Vf
vf 
mB vB
(m A  m B ) sin 
Gives
Vf = 48.6 kph
Can the investigators determine
who was speeding?
mB vB
vf 
(m A  m B ) sin 
mA= 830 kg
mB = 550 kg
mBvB
tan 
m Av A
http://www.physics.ubc.ca/~outreach/phys420/p420_96/danny/danweb.htm
m
v
v+ v
U = Vel.
of gas rel.
to rocket
Burns fuel at
a rate dm
dt
IN THE EARTH REF. FRAME
Vel of gas rel me = vel of gas rel. rocket - vel of rocket rel me
=U-v
Mom. of gas = m(U - v) = -change in mom. of
rocket (impulse)
i.e.
F dt = m(v - U) = v dm - U dm
F dt = m(v - U) = v dm - U dm
Now the force pushing the rocket is F = dprocket
i.e.
dt
Note  m dv since
dt
m is not constant
d
F  (mv )
dt
dm
dv

v m
dt
dt
Fdt = v dm + m dv
so that v dm + m dv = v dm - U dm
dm
dv = -U
m
This means that if I throw out dm of gas with vel. U,
I will increase rocket velocity by dv.
dm
dv = -U
m
This means that if I throw out dm of gas with vel. U,
I will increase rocket velocity by dv.
If I want to find out the TOTAL effect of throwing out gas,
from when the mass was mi and velocity was vi, to the time
when the mass is mf and the velocity vf, I must integrate.
vf
mi 1
dm
Thus
 dv  U 
vi
mi m
1
mf
[ v ]vf


U
[ln
m
]
note
 dm  ln m
vi
mi
m
vf -vi = - U (ln mf - ln mi)
= + U (ln mi - ln mf)
if vi = 0
vf =
mi
U ln
mf
mi
vf = U ln
mf
Speed in units of gas velocity
2
Reducing mass
(mf = 0)
1
Constant mass
(v = at)
.2
.8
1
.6
.4
Fraction of mass burnt as fuel
An example
Mi = 850 kg
mf = 180 kg
Thrust = dp/dt of gas
= dm/dt U
U = 2800 m s-1
=2.3 x 2800
dm/dt = 2.3 kg s-1
= 6400 N
Initial acceleration F = ma ==> a = F/m
= 6400/850 = 7.6 m s-2
Final vel.
mi
v f  U ln
mf
850
 2800 ln
 4300 m s 1
180