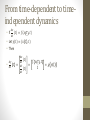* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Non-Holonomic Motion Planning
Derivations of the Lorentz transformations wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Four-vector wikipedia , lookup
Center of mass wikipedia , lookup
Fluid dynamics wikipedia , lookup
Hamiltonian mechanics wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Hooke's law wikipedia , lookup
Dynamical system wikipedia , lookup
Dynamic substructuring wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Lagrangian mechanics wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Differential (mechanical device) wikipedia , lookup
Mitsubishi AWC wikipedia , lookup
Analytical mechanics wikipedia , lookup
Centripetal force wikipedia , lookup
Classical central-force problem wikipedia , lookup
Routhian mechanics wikipedia , lookup
Virtual work wikipedia , lookup
Dynamics Kris Hauser I400/B659, Spring 2014 Agenda • • • • • Ordinary differential equations Open and closed loop controls Integration of ordinary differential equations Dynamics of a particle under force field Rigid body dynamics Dynamics • How a system moves over time as a reaction to forces and torques • Distinguished from kinematics, which purely describes states and geometric paths • Uncontrolled dynamics: • From initial conditions that include state x0 and time t0, the system evolves to produce a trajectory x(t). • Controlled dynamics: • From initial conditions x0, time t0, and given controls u(t), the system evolves to produce a trajectory x(t) Dynamic equations • x(t): state trajectory • (a function from real numbers to vectors) • Uncontrolled dynamic equation: • 𝑑𝑥 𝑑𝑡 𝑡 = 𝑓(𝑥 𝑡 , 𝑡) • An ordinary differential equation (ODE) Dynamic equations • x(t): state trajectory • (a function from real numbers to vectors) • Uncontrolled dynamic equation: • 𝑑𝑥 𝑑𝑡 𝑡 = 𝑓(𝑥 𝑡 , 𝑡) • An ordinary differential equation (ODE) • Example: point mass with gravity g • Position is 𝑝(𝑡) = 𝑝𝑥 (𝑡), 𝑝𝑦 (𝑡) • Acceleration (f=ma) is 𝑑 2 𝑝𝑦 (𝑡) 𝑑𝑡 2 = −𝑔/𝑚 Dynamic equations • x(t): state trajectory • (a function from real numbers to vectors) • Uncontrolled dynamic equation: • 𝑑𝑥 𝑑𝑡 𝑡 = 𝑓(𝑥 𝑡 , 𝑡) • An ordinary differential equation (ODE) • Example: point mass with gravity g • Position is 𝑝(𝑡) = 𝑝𝑥 (𝑡), 𝑝𝑦 (𝑡) • Acceleration (f=ma) is 𝑑 2 𝑝𝑦 (𝑡) 𝑑𝑡 2 = −𝑔/𝑚 • Uh… how do we work with this? • Second-order differential equation From second-order ODEs to first-order ODEs • Let 𝑥(𝑡) = (𝑝(𝑡), 𝑣(𝑡)) with 𝑣(𝑡) = • Then • 𝑑𝑥 𝑑𝑡 𝑡 = 𝑑𝑝 (𝑡) 𝑑𝑡 𝑑𝑣 (𝑡) 𝑑𝑡 𝑑𝑝 𝑡 𝑑𝑡 From second-order ODEs to first-order ODEs • Let 𝑥(𝑡) = (𝑝(𝑡), 𝑣(𝑡)) with 𝑣(𝑡) = 𝑑𝑝 𝑡 𝑑𝑡 • Then • 𝑑𝑥 𝑑𝑡 𝑡 = 𝑑𝑝 (𝑡) 𝑑𝑡 𝑑𝑣 (𝑡) 𝑑𝑡 = 𝑣 𝑡 𝐺 𝑚 = 𝑓 𝑥 𝑡 ,𝑡 0 −𝑔 • If p is d dimensional, x is 2d-dimensional • Here G is the gravity vector From time-dependent to timeindependent dynamics • If 𝑑𝑥 (𝑡) 𝑑𝑡 = 𝑓(𝑥 𝑡 , 𝑡) • Let y(𝑡) = (𝑥 𝑡 , 𝑡) • Then • 𝑑𝑦 𝑑𝑡 𝑡 = 𝑑𝑥 (𝑡) 𝑑𝑡 𝑑𝑡 (𝑡) 𝑑𝑡 = 𝑓 𝑥 𝑡 ,𝑡 1 =𝑔 𝑦 𝑡 Dynamic equation as a vector field • Can ask: • From some initial condition, on what trajectory does the state evolve? • Where will states from some set of initial conditions end up? • Point (convergence), a cycle (limit cycle), or infinity (divergence)? Numerical integration of ODEs • If h, 𝑑𝑥 (𝑡) 𝑑𝑡 = 𝑓(𝑥(𝑡)) and x(0) are known, then given a step size • 𝑥 𝑘ℎ 𝑥𝑘 = 𝑥𝑘−1 + ℎ 𝑓(𝑥𝑘−1 ) • gives an approximate trajectory for k 1 • Provided f is smooth • Accuracy depends on h • Known as Euler’s method Integration errors • Lower error with smaller step size • Consider system whose limit cycle is a circle • 𝑑𝑥 𝑑𝑡 𝑑𝑦 𝑑𝑡 −𝑦 = 𝑥 • Euler integrator diverges for all step sizes! • Better integration schemes are available • (e.g., Runge-Kutta methods, implicit integration, adaptive step sizes, energy conservation methods, etc) • Beyond the scope of this course Open vs. Closed loop • Open loop control: • The controls u(t) only depend on time, not x(t) • E.g., a planned path, sent to the robot • No ability to correct for unexpected errors • Closed loop control : • The controls u(x(t),t) depend both on time and x(t) • Feedback control • Requires the ability to measure x(t) (to some extent) • In either case we have an ODE, once we have chosen the control function st Controlled Dynamics -> 1 order time-independent ODE • Open loop case: • If • 𝑑𝑥 (𝑡) 𝑑𝑡 𝑑𝑦 𝑑𝑡 = 𝑓(𝑥 𝑡 , 𝑢(𝑡)), then let y(t)=(x(t),t) 𝑡 = 𝑓 𝑥 𝑡 ,𝑢 𝑡 1 =𝑔 𝑦 𝑡 st Controlled Dynamics -> 1 order time-independent ODE • Open loop case: • If • 𝑑𝑥 (𝑡) 𝑑𝑡 = 𝑓(𝑥 𝑡 , 𝑢(𝑡)), then let y(t)=(x(t),t) 𝑡 = 𝑓 𝑥 𝑡 ,𝑢 𝑡 1 𝑑𝑦 𝑑𝑡 =𝑔 𝑦 𝑡 • Closed loop case: 𝑑𝑥 • If 𝑑𝑡 (𝑡) = 𝑓(𝑥 𝑡 , 𝑢(𝑥 𝑡 , 𝑡)), then let y(t)=(x(t),t) • 𝑑𝑦 𝑑𝑡 𝑡 = 𝑓 𝑥 𝑡 ,𝑢 𝑥 𝑡 ,𝑡 1 =𝑔 𝑦 𝑡 st Controlled Dynamics -> 1 order time-independent ODE • Open loop case: • If • 𝑑𝑥 (𝑡) 𝑑𝑡 = 𝑓(𝑥 𝑡 , 𝑢(𝑡)), then let y(t)=(x(t),t) 𝑡 = 𝑓 𝑥 𝑡 ,𝑢 𝑡 1 𝑑𝑦 𝑑𝑡 =𝑔 𝑦 𝑡 • Closed loop case: 𝑑𝑥 • If 𝑑𝑡 (𝑡) = 𝑓(𝑥 𝑡 , 𝑢(𝑥 𝑡 , 𝑡)), then let y(t)=(x(t),t) • 𝑑𝑦 𝑑𝑡 𝑡 = 𝑓 𝑥 𝑡 ,𝑢 𝑥 𝑡 ,𝑡 1 =𝑔 𝑦 𝑡 • How do we choose u? A subject for future classes DYNAMICS OF RIGID BODIES Rigid Body Dynamics • The following can be derived from first principles using Newton’s laws + rigidity assumption • Parameters • • • • • CM translation c(t) CM velocity v(t) Rotation R(t) Angular velocity w(t) Mass m, local inertia tensor HL Rigid body ordinary differential equations • We will express forces and torques in terms of terms of H (a function of R), 𝜔, 𝑣 and 𝜔 • 𝑓 = 𝑚𝑣 • 𝜏 = [𝜔] 𝐻 𝜔 + 𝐻 𝜔 • Rearrange… • 𝑣 = 𝑓/𝑚 • 𝜔 = 𝐻 −1 (𝜏 − 𝜔 𝐻 𝜔 ) • So knowing f(t) and τ(t), we can derive c(t), v(t), R(t), and w(t) by solving an ordinary differential equation (ODE) • dx/dt = f(x) • x(0) = x0 • With x=(c,v,R,w) the state of the rigid body Kinetic energy for rigid body • Rigid body with velocity v, angular velocity w • KE = ½ (m vTv + wT H w) • World-space inertia tensor H = R HL RT 1/2 w v T H 0 0 mI w v Kinetic energy derivatives • 𝜕𝐾𝐸 𝜕𝑣 = 𝑚𝑣 • Force (@CM) 𝑓 = • • 𝜕𝐾𝐸 𝜕𝜔 𝑑 H 𝑑𝑡 𝑑 𝜕𝐾𝐸 ( ) 𝑑𝑡 𝜕𝑣 = 𝑚𝑣 = 𝐻𝜔 = [w]H – H[w] • Torque t = 𝑑 𝜕𝐾𝐸 𝑑𝑡 𝜕𝜔 = [w] H w + H 𝜔 Summary •𝑓 = 𝑚𝑣 • 𝜏 = [𝜔] 𝐻 𝜔 + 𝐻 𝜔 Gyroscopic “force” Force off of COM F x Force off of COM F 𝛿𝑥 x Consider infinitesimal virtual displacement 𝛿𝑥 generated by F. (we don’t know what this is, exactly) The virtual work performed by this displacement is FT𝛿𝑥 Generalized torque f Now consider the equivalent force f, torque τ at COM Generalized torque f 𝛿𝑥 𝛿𝑞 Now consider the equivalent force f, torque τ at COM And an infinitesimal virtual displacement of R.B. coordinates 𝛿𝑞 Generalized torque f 𝛿𝑥 𝛿𝑞 Now consider the equivalent force f, torque τ at COM And an infinitesimal virtual displacement of R.B. coordinates 𝛿𝑞 Virtual work in configuration space is [fT,τT] 𝛿𝑞 Principle of virtual work f F 𝛿𝑥 𝛿𝑞 [fT,τT] 𝛿𝑞= FT 𝛿𝑥 Since 𝛿𝑥 = 𝐽 𝑞 𝛿𝑞 we have [fT,τT] 𝛿𝑞= FT𝐽 𝑞 𝛿𝑞 Principle of virtual work f F 𝛿𝑥 𝛿𝑞 [fT,τT] 𝛿𝑞= FT 𝛿𝑥 Since 𝛿𝑥 = 𝐽 𝑞 𝛿𝑞 we have [fT,τT] 𝛿𝑞= FT𝐽 𝑞 𝛿𝑞 Since this holds no matter what 𝛿𝑞 is, we have [fT,τT] = FTJ(q), f Or JT(q) F = τ Next class • Feedback control • Principles App J