Download Dynamics_NewtonLaws - University of Manchester

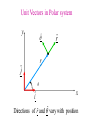
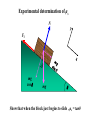
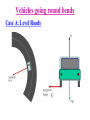
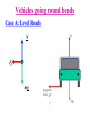
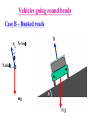
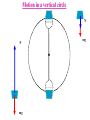
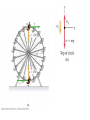
Dynamics
Dynamics
Velocity &
Acceleration
Inertial Frames
Forces –
Newton’s Laws
Part I - “I frame no hypotheses;
for whatever is not deduced from
the phenomena is to be called a
hypothesis; and hypotheses,
whether metaphysical or physical,
whether of occult qualities or
mechanical, have no place in
experimental philosophy.”
READ the
Textbook!
http://www.hep.manchester.ac.uk/u/parkes/Chris_Parkes/Teaching.html
October 2013
Chris Parkes
vector addition
• c=a+b
y
cx= ax +bx
cy= ay +by
b
can use unit vectors i,j
a
c
i vector length 1 in x direction
x
j vector length 1 in y direction
scalar product
finding the angle between two vectors
a  b  ab cos  a x bx  a y by a,b, lengths of a,b
Result is a scalar
a xbx  a y by
a b
cos 

2
2
2
2
ab
a x  a y  bx  by
a

b
Vector product
e.g. Find a vector perpendicular to two vectors
c  ab
c  a b sin 
iˆ
c  a  b  ax
bx
ˆj
ay
by
kˆ  a y bz  a z by 


a z   a z bx  a x bz 
bz  a x by  a y bx 
c
Right-handed
Co-ordinate system
b

a
Unit Vectors in Polar system
y
ˆ
r̂
r
ĵ
θ
iˆ
x
Directions of rˆ and ˆ vary with position
y
ĵ
ˆ
r̂
ˆ cos
θ


r̂ cos
 ˆ sin 
ĵ
rˆ  cos  iˆ  sin  ˆj
r̂ sin 
iˆ
ˆ   sin  iˆ  cos  ˆj
r
iˆ
x
The component of
The component of
r̂
r̂ in the x direction =
in the y direction =
The component of ˆ in the x direction =
The component of
ˆ in the y direction =
r̂ cos   cos
r̂ sin   sin 
 ˆ sin    sin 
ˆ cos   cos 
Velocity and acceleration vectors
• Position changes with time
• Rate of change of r is
velocity
Y
(x,y) or (r,θ)
– How much is the change in a
very small amount of time t
v
d r r (t  t )  r (t )
Limit at  t0

dt
t
v = rr̂ + rqqˆ
dv v(t + dt) - v(t) d 2 r
a=
=
= 2
dt
dt
dt
a = (r - rq 2 )r̂ + (2rq + rq )qˆ
r(t)
0
x
r(t+t)
X
v  rrˆ  rˆ
Geometric interpretation of this equation
Radial component
Tangential component
Relative Velocity 1D
e.g. Alice walks forwards along a boat at 1m/s and the boat moves at 2m/s.
What is Alice’s velocity as seen by Bob ?
If Bob is on the boat it is just 1 m/s
If Bob is on the shore it is 1+2=3m/s
If Bob is on a boat passing in the opposite direction….. and the earth is
moving around the sun…
Velocity relative to an observer
Relative Velocity 2D
e.g. Alice walks across the boat at 1m/s.
V boat 2m/s
As seen on the shore:
θ
V
2
2
V  1  2  5m / s relative to shore
tan   1 / 2,  27
V Alice 1m/s
Changing co-ordinate system
y
Define the frame of reference – the co-ordinate system –
in which you are measuring the relative motion.
No ‘correct’ or ‘preferred’ frame
(x’,y’) Frame S’
(boat) v boat w.r.t shore
Frame S
(shore)
vt
x’
x
Equations for (stationary) Alice’s position on boat w.r.t shore
i.e. the co-ordinate transformation from frame S to S’
x=
Assuming S and S’ coincide at t=0 :
Known as Gallilean transformations
These simple relations do not hold in special relativity
x '+ vt
y = y' , t = t '
dx
dx '
=
dt
dt + v
We described the motion, position,
velocity, acceleration,
now look at the underlying causes
Newton’s laws
• First Law
– A body continues in a state of rest or uniform
motion unless there are forces acting on it.
• No external force means no change in velocity
• Second Law
– A net force F acting on a body of mass m [kg]
produces an acceleration a = F /m [ms-2]
• Relates motion to its cause
F = ma
units of F: kg.m.s-2, called Newtons [N]
• Third Law
– The force exerted by A on B is equal and opposite to
the force exerted by B on A
Fb
•Force exerted by
block on table is Fa
Block on table
Fa=-Fb
Weight
(a Force)
Fa
•Force exerted by
table on block is Fb
(Both equal to weight)
Examples of Forces
weight of body from gravity (mg),
- remember m is the mass, mg is the force (weight)
tension, compression
friction, fluid resistance
Force Components
•Force is a Vector
•Resultant from vector sum
R  F1  F2
F1
R
F2
•Resolve into perpendicular components
Fx  F cos 
Fy
F
Fy  F sin 

F x  Fxiˆ
F y  Fy ˆj
Fx
Free Body Diagram
• Apply Newton’s laws to particular body
• Only forces acting on the body matter
– Net Force
F
• Separate problem into each body
e.g.
Body 1
Supporting Force
from plane
(normal
force)
Friction
Tension
In rope
Block weight
Body 2
Tension in rope
Block Weight
Tension & Compression
• Tension
– Pulling force - flexible or rigid
• String, rope, chain and bars
mg
• Compression
– Pushing force
• Bars
mg
mg
• Tension & compression act in BOTH
directions.
– Imagine string cut
– Two equal & opposite forces – the tension
Friction
• A contact force resisting sliding
– Origin is electrical forces between atoms in the two
surfaces.
• Static Friction (fs)
– Must be overcome before an objects starts to move
• Kinetic Friction (fk)
– The resisting force once sliding has started
• does not depend on speed
N
fs or fk
F
mg
fs  s N
fk  k N
Friction – origin, values
• Friction proportional to N is an approximate rule
• Microscopic level
– Intermolecular forces where surfaces come into contact
– Once sliding starts usually easier to keep in motion
• Less bonding, kinetic < static friction
Material
Steel on steel
Glass on Glass
Teflon on Teflon
Rubber on concrete (dry)
Rubber on concrete (wet)
Static Coefficient
0.74
0.94
0.04
1.0
0.30
Kinetic Coefficient
0.57
0.40
0.04
0.8
0.25
Experimental determination of μs
N
Ff

mg
cos
mg

Show that when the block just begins to slide , μs = tanθ
The Rotor Fairground Ride
What does the speed of the Rotor need to be before the floor is removed?
Vehicles going round bends
Case A: Level Roads
Ff
Vehicles going round bends
Case A: Level Roads
N
Ff
mg
F
f
Vehicles going round bends
Case B – Banked roads
N N cos

N sin
mg
Motion in a vertical circle
N
N
mg
mg
Looping the Loop
In a 1901 circus performance, Allo ‘Dare Devil’ Diavolo introduced the stunt
of riding a bicycle in a loop the loop. Assuming that the loop is a circle of
radius R = 2.7m, what is the minimum speed Diavolo could have at the top
of the loop in order to complete the stunt successfully?
Revision / Summary: Newton III
• Newton III Pairs act on different bodies
– A on B, B on A
– e.g. Earth pulls book down, book pulls Earth up
FTB
FBT
FEB
FBE
N.III Pairs:
FTB = -FBT
FEB = -FBE
(aE=FBE/mE, tiny)
Revision / Summary: Newton II Problems
1.
2.
3.
4.
5.
6.
7.
Draw a simple sketch of the system to be analysed.
Identify the individual objects to which Newton’s 2nd Law
can be applied.
For each object draw a free-body diagram showing all the
forces acting on the object.
Introduce a co-ordinate system for each object.
For each object, determine the components of the forces
along each of the object’s co-ordinate axes.
For each object, write a separate equation for each
component of Newton’s 2nd Law ( equation of motion).
Solve the equations of motion.
Tension
(normal
In rope
Free Body force)
Diagram
Friction
Block weight
backup
A passenger on a Ferris
wheel moves in a
vertical circle of radius
R with constant speed,
v. Assuming the seat
remains upright during
the motion, derive
expressions for the
force the seat exerts on
the passenger at the top
of the circle and at the
bottom.
A small bead can slide without
friction on a circular hoop that is
in a vertical plane and has a
radius of 0.1 m. The hoop rotates
at a constant rate of 4 revs/s about
a vertical diameter.
(a) Find the angle β at which the
bead is in vertical equilibrium.
(b) Is it possible for the bead to
‘ride’ at the same elevation as the
centre of the hoop?
(c) What will happen if the hoop
rotates at 1 rev/s ?