* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Numerical weather prediction wikipedia , lookup
Computer simulation wikipedia , lookup
Theoretical ecology wikipedia , lookup
Plateau principle wikipedia , lookup
Atomic theory wikipedia , lookup
Computational fluid dynamics wikipedia , lookup
Generalized linear model wikipedia , lookup
History of numerical weather prediction wikipedia , lookup
Terms Test 1 - Wednesday, 13/08/2014, 5pm
• MCLT101 and 103
•
Event Name: ENGR110 Test
•
Event Type: Terms test
•
Date(s): Wednesday, 13/08/2014
•
Time: 17:10-18:00
•
Will alcohol be served? No
•
Will the VC Attend? No
•
Other Information: Co345
• FSMs
• Physical Modelling
• Worth 10% of course mark
• 50 Minute duration
• Arrive at 5:00 for 5:10 start
• No notes allowed
• Calculators allowed
Physical Modelling:
1.
2.
3.
4.
5.
6.
Out there world inside here
Modelling
Practical example: Passive Dynamic Walkers
Base systems and concepts
Ideals, assumptions and real life
Similarities in systems and responses
F1 F2
Design Cycle:
https://stillwater.sharepoint.okstate.edu/ENGR1113/default.aspx
How to Model Physical Systems
• Scale physical model
• Mathematical model
• Numerical model
www.autospeed.com
Modelling of Physical Systems
• Develop mathematical models, i.e. ordinary differential equations,
that describe the relationship between input and output
characteristics of a system.
• These equations can then be used to forecast the behaviour of the
system under specific conditions.
• All systems can normally be approximated and modelled by one of
several models, e.g.: mechanical, electrical, thermal or fluid.
We also find that we can translate a system from one model to
another to facilitate the modelling.
Lumped Parameter Models
• Use standard laws of physics and break a
system down into a number of building
blocks.
• Each of the parameters (property or
function) is considered independently.
www.brains-minds-media.org
http://www.3me.tudelft.nl/en/about-the-faculty/departments/biomechanicalengineering/research/dbl-delft-biorobotics-lab/bipedal-robots/
http://www.cyberphysics.co.uk/
Linear Time Invariant Models
• Assume the property of linearity for these
models.
•
A linear system will posses two properties;
1. Superposition
2. Homogeneity.
Allows us to use standard mathematical
operations to simplify our models
www.redlinemotive.com
Linear Time Invariant Models
• Assume system is time-invariant
• Constants stay constant in the time-scales of
our model
• Proportionality between variables does not
change.
Our shock absorbers do not wear in our car
suspension model!
Competition
tyres
Elements of Systems are Ideal
• Each element completely describes a property
• Elements are:
• Ideal
• Linear
• Represent only one property
The Spring Element
Represents the elastic properties (energy storage) in a system.
Assume:
•
No mass
•
No Fraction
•
Linear
The Spring Element
Hooke’s Law:
f(t) =
K=
x1 =
f(t) = K(x1 – x2) = Kx(t)
force applied to the ends of the spring,
spring constant (N.m)
or C = 1/K is the spring compliance,
Displacement of the one end, x2 = Displacement of the other end,
x = x1 – x2 = relative displacement of the two ends.
Rotational spring element torque T(t) in terms of the angular
displacement :
T(t) = K(1 - 2) = K(t)
T(t) = Torque
(t) = angular displacement
The Spring Element
Work done for a force, f, to move a spring a distance, dx:
W = f . dx
The energy then stored in the spring when the ends are displaced a distance x0 from the
equilibrium position is:
Es
xo
0
1 2 1 2
Kxdx Kx0 Cf 0
2
2
The Spring Element
Real springs show deviation from ideality:
• Real springs would have an associated mass, leading to the deviations in the step
and sinusoidal response as described before.
• Real springs will always contain some friction (energy dissipation) which is
exhibited in the non-coincidence of the loading – unloading curves.
• Real springs will always exhibit a degree of non-linearity (deviation from f = Kx).
See section on linearisation.
Energy losses in
real springs
Several types of practical springs
marccardaronella.com
Linearisation
Many elements show non-linear behaviour.
To use in our relatively simple models, we must first linearise this element around an
operating point.
Get a linear model that should be valid for small excursions from this operating point.
Consider a non-linear coil spring that forms part of the
suspension system of an automobile.
Operating point = Equilibrium position under load
The Damper Element
Damper element (dashpot) represents the forces opposing motion, i.e. the
friction or damping effects.
Damping force is proportional to the velocity of the piston.
The Damper Element
dx
dx1 dx2
f fv
fvv
fv
dt
dt
dt
http://www.flotronicpumps.co.uk/
where f = force applied to the ends of the damper,
dx/dt = v = relative velocity of the plunger
fv = coefficient of viscous friction or simply called the
damping coefficient
www.modified.com
The Mass (inertia) Element
All real elements will have some mass, so that the mass element in the model will thus
represent the physical mass of the system.
This element represents the inertia or resistance to acceleration of the system.
The mass element will be modelled as concentrated at a point.
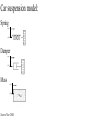
Car suspension model:
• Mechanical system
Explain what happens when a car
goes over a bump?
www.superbike-coach.com
Car suspension model:
Explain what happens when a car
goes over a bump?
Simplify to single-inputsingle-output system
Form individual component models
Determine their relationships (use physical laws!)
Combine (and simplify if possible)
x
This gives us an instantaneous differential equation, but
want a time response!
finput
Car suspension model:
Force - Distance
Spring
x t
f s t Kxt
f t
Damper
x t
f t
Mass
x t
f t
Source Nise 2004
dxt
f c t C
dt
d 2 xt
f m t M
dt 2
f input t f s t f d t f m t
dxt
d 2 xt
f input t Kxt C
m
dt
dt 2
This gives us an instantaneous differential
equation, but want a time response!
Integrate:
• numerically
• theoretically
• using tables
9
8
clf; %clear all graphs
7
K = 10 %Spring constant
m = 1 %mass (constant)
Distance x (m)
C = 3 %Damping constant
6
5
4
3
t = [0: 0.01: 20];%set up the time increments
2
1
stept = 1 + 0*t; %graph to show step response
plot(t,stept,'m');
1.5
0
0
2
4
6
8
10
12
Time t (s)
14
16
18
20
xlabel('Time t (s)')
ylabel('Distance x (m)')
hold on % put each graph on top of each other
Distance x (m)
1
0.5
for C = 1.0: 1: 10.0
d = tf(9,[m C K])
1.5
0
0
2
4
6
8
10
12
Time t (s)
14
16
18
20
2
4
[y,t]=step(d,T);%step response over one second
pause(2)
end
1
Distance x (m)
plot(t,y,'k');
0.5
0
0
6
8
10
12
Time t (s)
14
16
18
20