Download Practice Exercise

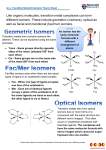
Sample Exercise 24.1 Identifying the Coordination Sphere of a Complex
Palladium(II) tends to form complexes with a coordination number of 4. One such compound was originally
formulated as PdCl2 · 3 NH3. (a) Suggest the appropriate coordination compound formulation for this
compound. (b) Suppose an aqueous solution of the compound is treated with excess AgNO 3(aq). How many
moles of AgCl(s) are formed per mole of PdCl2 · 3 NH3?
Solution
Analyze: We are given the coordination number of Pd(II) and a chemical formula indicating that NH 3 and
Cl– are the potential ligands. We are asked to determine (a) what ligands are attached to Pd(II) in the
compound and (b) how the compound behaves toward AgNO3 in aqueous solution.
Plan: (a) Because of their charge, the Cl– ions can be either in the coordination sphere, where they are
bonded directly to the metal, or outside the coordination sphere, where they are bonded ionically to the
complex. Because the NH3 ligands are neutral, they must be in the coordination sphere. (b) The chlorides
that are in the coordination sphere will not be precipitated as AgCl.
Solve:
(a) By analogy to the ammonia complexes of cobalt(III), we predict that the three NH 3 groups of PdCl2 · 3
NH3 serve as ligands attached to the Pd(II) ion. The fourth ligand around Pd(II) is one of the chloride ions.
The second chloride ion is not a ligand; it serves only as an anion in this ionic compound. We conclude that
the correct formulation is [Pd(NH3)3Cl]Cl.
(b) The chloride ion that serves as a ligand will not be precipitated as AgCl(s) following
the reaction with AgNO3(aq). Thus, only the single “free” Cl– can react. We therefore expect to produce 1
mol of AgCl(s) per mole of complex. The balanced equation is [Pd(NH3)3Cl]Cl(aq) +
AgNO3(aq) → [Pd(NH3)3Cl]NO3(aq) + AgCl(s). This is a metathesis reaction (Section 4.2) in which one of
the cations is the [Pd(NH3)3Cl]+ complex ion.
Chemistry: The Central Science, Eleventh Edition
By Theodore E. Brown, H. Eugene LeMay, Bruce E. Bursten, and Catherine J. Murphy
With contributions from Patrick Woodward
Copyright ©2009 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Sample Exercise 24.1 Identifying the Coordination Sphere of a Complex
Practice Exercise
Predict the number of ions produced per formula unit in an aqueous solution of CoCl 2· 6 H2O.
Answer: three (the complex ion, [Co(H2O)6]2+, and two chloride ions)
Chemistry: The Central Science, Eleventh Edition
By Theodore E. Brown, H. Eugene LeMay, Bruce E. Bursten, and Catherine J. Murphy
With contributions from Patrick Woodward
Copyright ©2009 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Sample Exercise 24.2 Determining the Oxidation Number of a Metal in a Complex
What is the oxidation number of the central metal in [Rh(NH 3)5Cl](NO3)2?
Solution
Analyze: We are given the chemical formula of a coordination compound, and we are asked to determine
the oxidation number of its metal atom.
Plan: To determine the oxidation number of the Rh atom, we need to figure out what charges are
contributed by the other groups in the substance. The overall charge is zero, so the oxidation number of the
metal must balance the charge that is due to the rest of the compound.
Solve: The NO3 group is the nitrate anion, which has a 1– charge, NO3–. The NH3 ligands are neutral, and
the Cl is a coordinated chloride ion, which has a 1– charge, Cl–. The sum of all the charges must be zero.
The oxidation number of rhodium, x, must therefore be +3.
Practice Exercise
What is the charge of the complex formed by a platinum(II) metal ion surrounded by two ammonia molecules
and two bromide ions?
Answer: zero
Chemistry: The Central Science, Eleventh Edition
By Theodore E. Brown, H. Eugene LeMay, Bruce E. Bursten, and Catherine J. Murphy
With contributions from Patrick Woodward
Copyright ©2009 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Sample Exercise 24.3 Determining the Formula of a Complex Ion
A complex ion contains a chromium(III) bound to four water molecules and two chloride ions. What is its
formula?
Solution
Analyze: We are given a metal, its oxidation number, and the number of ligands of each kind in a complex
ion containing the metal, and we are asked to write the chemical formula of the ion.
Plan: We write the metal first, then the ligands. We can use the charges of the metal ion and ligands to
determine the charge of the complex ion. The oxidation state of the metal is +3, water is neutral, and
chloride has a 1– charge.
Solve:
The charge on the ion is 1+, [Cr(H2O)4Cl2]+.
Practice Exercise
Write the formula for the complex described in the Practice Exercise accompanying Sample Exercise 24.2.
Answer: [Pt(NH3)2Br2]
Chemistry: The Central Science, Eleventh Edition
By Theodore E. Brown, H. Eugene LeMay, Bruce E. Bursten, and Catherine J. Murphy
With contributions from Patrick Woodward
Copyright ©2009 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Sample Exercise 24.4 Naming Coordination Compound
Name the following compounds: (a) [Cr(H2O)4Cl2]Cl, (b) K4[Ni(CN)4].
Solution
Analyze: We are given the chemical formulas for two coordination compounds, and we are assigned the task of
naming them.
Plan: To name the complexes, we need to determine the ligands in the complexes, the names of the ligands, and
the oxidation state of the metal ion. We then put the information together following the rules listed previously.
Solve: (a) As ligands, there are four water
molecules, which are indicated as tetraaqua,
and two chloride ions, indicated as dichloro.
The oxidation state of Cr is +3.
Thus, we have chromium(III). Finally, the anion
is chloride. Putting these parts together, the
name of the compound is
(b) The complex has four cyanide ions, CN–,
as ligands, which we indicate as tetracyano.
The oxidation state of the nickel is zero.
Becausethe complex is an anion, the metal is indicated
as nickelate(0). Putting these partstogether and
naming the cation first, we have
Practice Exercise
Name the following compounds: (a) [Mo(NH3)3Br3]NO3, (b) (NH4)2[CuBr4]. (c) Write the formula for sodium
diaquabis(oxalato)ruthenate(III).
Answers: (a) triamminetribromomolybdenum(IV) nitrate, (b) ammonium tetrabromocuprate(II)
(c) Na[Ru(H2O)2(C2O4)2]
Chemistry: The Central Science, Eleventh Edition
By Theodore E. Brown, H. Eugene LeMay, Bruce E. Bursten, and Catherine J. Murphy
With contributions from Patrick Woodward
Copyright ©2009 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Sample Exercise 24.5 Determining the Number of Geometric Isomers
The Lewis structure of the CO molecule indicates that the molecule has a lone pair of electrons on the C atom
and one on the O atom
. When CO binds to a transition-metal atom, it nearly always does so by
using the lone pair on the C atom. How many geometric isomers are there for tetracarbonyldichloroiron(II)?
Solution
Analyze: We are given the name of a complex containing only monodentate ligands, and we must determine
the number of isomers the complex can form.
Plan: We can count the number of ligands, thereby determining the coordination number of the Fe in the
complex and then use the coordination number to predict the geometry of the complex. We can then either
make a series of drawings with ligands in different positions to determine the number of isomers, or we can
deduce the number of isomers by analogy to cases we have discussed.
Solve: The name indicates that the complex has four carbonyl (CO) ligands and two chloro (Cl –) ligands, so
its formula is Fe(CO)4Cl2. The complex therefore has a coordination number of 6, and we can assume that it
has an octahedral geometry. Like [Co(NH3)4Cl2 ]+ (Figure 24.1), it has four ligands of one type and two of
another. Consequently, it possesses two isomers: one with the Cl – ligands across the metal from each other
(trans-Fe(CO)4Cl2) and one with the Cl– ligands adjacent (cis-Fe(CO)4Cl2).
In principle, the CO ligand could exhibit linkage isomerism by binding to a metal atom via the lone pair on
the O atom. When bonded this way, a CO ligand is called an isocarbonyl ligand. Metal isocarbonyl
complexes are extremely rare, and we do not normally have to consider the possibility that CO will bind in
this way.
Comment: It is easy to overestimate the number of geometric isomers. Sometimes different orientations of
a single isomer are incorrectly thought to be different isomers. If two structures can be rotated so that they
are equivalent, they are not isomers of each other. The problem of identifying isomers is compounded by the
difficulty we often have in visualizing three-dimensional molecules from their two-dimensional
representations. It is sometimes easier to determine the number of isomers if we use three-dimensional
models.
Chemistry: The Central Science, Eleventh Edition
By Theodore E. Brown, H. Eugene LeMay, Bruce E. Bursten, and Catherine J. Murphy
With contributions from Patrick Woodward
Copyright ©2009 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Sample Exercise 24.5 Determining the Number of Geometric Isomers
Practice Exercise
How many isomers exist for square-planar [Pt(NH3)2ClBr]?
Answer: two
Chemistry: The Central Science, Eleventh Edition
By Theodore E. Brown, H. Eugene LeMay, Bruce E. Bursten, and Catherine J. Murphy
With contributions from Patrick Woodward
Copyright ©2009 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Sample Exercise 24.6 Predicting Whether a Complex Has Optical Isomers
Does either cis- or trans-[Co(en)2Cl2]+ have optical isomers?
Solution
Analyze: We are given the chemical formula for two structural isomers, and we are asked to determine
whether either one has optical isomers. The en ligand is a bidentate ligand, so the complexes are sixcoordinate and octahedral.
Plan: We need to sketch the structures of the cis and trans isomers and their mirror images. We can draw the
en ligand as two N atoms connected by a line, as is done in Figure 24.20. If the mirror image cannot be
superimposed on the original structure, the complex and its mirror image are optical isomers.
Solve: The trans isomer of [Co(en)2Cl2]+ and its mirror image is
where the dashed vertical line represents a mirror. Notice that the mirror image of the trans isomer is
identical to the original. Consequently trans-[Co(en)2Cl2 ]+ does not exhibit optical isomerism.
The mirror image of the cis isomer of [Co(en)2Cl2]+, however, cannot be superimposed on the original
Thus, the two cis structures are optical isomers (enantiomers): cis-[Co(en)2Cl2 ]+ is a chiral complex.
Chemistry: The Central Science, Eleventh Edition
By Theodore E. Brown, H. Eugene LeMay, Bruce E. Bursten, and Catherine J. Murphy
With contributions from Patrick Woodward
Copyright ©2009 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Sample Exercise 24.6 Predicting Whether a Complex Has Optical Isomers
Practice Exercise
Does the square-planar complex ion [Pt(NH3)(N3)ClBr]– have optical isomers?
Answer: no
Chemistry: The Central Science, Eleventh Edition
By Theodore E. Brown, H. Eugene LeMay, Bruce E. Bursten, and Catherine J. Murphy
With contributions from Patrick Woodward
Copyright ©2009 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Sample Exercise 24.7 Relating Color Absorbed to Color Observed
The complex ion trans-[Co(NH3)4Cl2]+ absorbs light primarily in the red region of the visible spectrum (the
most intense absorption is at 680 nm). What is the color of the complex?
Solution
Analyze: We need to relate the color absorbed by a complex (red) to the color observed for the complex.
Plan: The color observed for a substance is complementary to the color it absorbs. We can use the color
wheel of Figure 24.24 to determine the complementary color.
Solve: From Figure 24.24, we see that green is complementary to red, so the complex appears green.
Comment: As noted in Section 24.1, in the text discussing Table 24.1, this green complex
was one of those that helped Werner establish his theory of coordination. The other geometric isomer of this
complex, cis-[Co(NH3)4Cl2]+, absorbs yellow light and therefore appears violet.
Practice Exercise
The [Cr(H2O)6 ]2+ ion has an absorption band at about 630 nm. Which of the following colors—sky blue,
yellow, green, or deep red—is most likely to describe this ion?
Answer: sky blue
Chemistry: The Central Science, Eleventh Edition
By Theodore E. Brown, H. Eugene LeMay, Bruce E. Bursten, and Catherine J. Murphy
With contributions from Patrick Woodward
Copyright ©2009 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Sample Exercise 24.8 Using thenSpectrochemical Series
Which of the following complexes of Ti3+ exhibits the shortest wavelength absorption in the visible spectrum:
[Ti(H2O)6 ]3+, [Ti(en)3]3+, or [TiCl6]3–?
Solution
Analyze: We are given three octahedral complexes, each containing Ti in the +3 oxidation state. We need to
predict which complex absorbs the shortest wavelength of visible light.
Plan: Ti(III) is a d1 ion, so we anticipate that the absorption is due to a d-d transition in which the 3d
electron is excited from the lower-energy t2 set to the higher-energy e set. The wavelength of the light
absorbed is determined by the magnitude of the energy difference, Δ. Thus, we use the position of the
ligands in the spectrochemical series to predict the relative values of . The larger the energy, the shorter the
wavelength (Equation 24.7).
Solve: Of the three ligands involved—H2O, en, and Cl–—we see that ethylenediamine (en) is highest in the
spectrochemical series and will therefore cause the largest splitting, Δ, of the t2 and e sets of orbitals. The
larger the splitting, the shorter the wavelength of the light absorbed. Thus, the complex that absorbs the
shortestwavelength light is [Ti(en)3]3+.
Practice Exercise
The absorption spectrum of [Ti(NCS)6]3– shows a band that lies intermediate in wavelength between those for
[TiCl6]3– and [TiF6]3–. What can we conclude about the place of NCS– in the spectrochemical series?
Answer: It lies between Cl– and F–; that is, Cl– < NCS– < F–.
Chemistry: The Central Science, Eleventh Edition
By Theodore E. Brown, H. Eugene LeMay, Bruce E. Bursten, and Catherine J. Murphy
With contributions from Patrick Woodward
Copyright ©2009 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Sample Exercise 24.9 Predicting the Number of Unpaired Electrons in an
Octahedral Complex
Predict the number of unpaired electrons in six-coordinate high-spin and low-spin complexes of Fe3+ .
Solution
Analyze: We must determine how many unpaired electrons there are in the highspin and low-spin
complexes of the metal ion Fe3+.
Plan: We need to consider how the electrons populate d orbitals for Fe3+ when the metal is in an octahedral
complex. There are two possibilities: one giving a high-spin complex and the other giving a low-spin
complex. The electron configuration of Fe3+ gives us the number of d electrons. We then determine how
these electrons populate the t2 set and e set of d orbitals. In the high-spin case, the energy difference between
the t2 and e orbitals is small, and the complex has the maximum number of unpaired electrons. In the lowspin case, the energy difference between the t2 and e orbitals is large, causing the t2 orbitals to be filled
before any electrons occupy the e orbitals.
Solve: Fe3+ is a d5 ion. In a high-spin complex, all five of these electrons are unpaired, with three in the t2
orbitals and two in the e orbitals. In a low-spin complex, all five electrons reside in the t2 set of d orbitals, so
there is one unpaired electron:
Practice Exercise
For which d electron configurations in octahedral complexes is it possible to distinguish between high-spin
and low-spin arrangements?
Answer: d4, d5, d6, d7
Chemistry: The Central Science, Eleventh Edition
By Theodore E. Brown, H. Eugene LeMay, Bruce E. Bursten, and Catherine J. Murphy
With contributions from Patrick Woodward
Copyright ©2009 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Sample Exercise 24.10 Populating d Orbitals in Tetrahedral and Square-Planar
Complexes
Four-coordinate nickel(II) complexes exhibit both square-planar and tetrahedral geometries. The tetrahedral
ones, such as [NiCl4]2–, are paramagnetic; the square-planar ones, such as [Ni(CN)4]2–, are diamagnetic. Show
how the d electrons of nickel(II) populate the d orbitals in the appropriate crystal-field splitting diagram in
each case.
Solution
Analyze: We are given two complexes containing Ni2+, a tetrahedral one and a square-planar one. We are
asked to use the appropriate crystal-field diagrams to describe how the d electrons populate the d orbitals in
each case.
Plan: We need to first determine the number of d electrons possessed by Ni2+ and then use Figure 24.34 for
the tetrahedral complex and Figure 24.35 for the squareplanar complex.
Solve: Nickel(II) has an electron configuration of [Ar]3d8. The population of the d electrons in the two
geometries is
Comment: Notice that the tetrahedral complex is paramagnetic with two unpaired electrons, whereas the
square-planar complex is diamagnetic. Nickel(II) forms octahedral complexes more frequently than squareplanar ones, whereas heavier d8 metals tend to favor square planar coordination.
Chemistry: The Central Science, Eleventh Edition
By Theodore E. Brown, H. Eugene LeMay, Bruce E. Bursten, and Catherine J. Murphy
With contributions from Patrick Woodward
Copyright ©2009 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Sample Exercise 24.10 Populating d Orbitals in Tetrahedral and Square-Planar
Complexes
Practice Exercise
How many unpaired electrons do you predict for the tetrahedral [CoCl 4]2– ion?
Answer: three
Chemistry: The Central Science, Eleventh Edition
By Theodore E. Brown, H. Eugene LeMay, Bruce E. Bursten, and Catherine J. Murphy
With contributions from Patrick Woodward
Copyright ©2009 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Sample Integrative Exercise Putting Concepts Together
The oxalate ion has the Lewis structure shown in Table 24.2. (a) Show the geometrical structure of the
complex formed by coordination of oxalate to cobalt(II), forming [Co(C 2O4)(H2O)4]. (b)Write the formula for
the salt formed upon coordination of three oxalate ions to Co(II), assuming that the charge-balancing cation is
Na+. (c) Sketch all the possible geometric isomers for the cobalt complex formed in part (b). Are any of
these isomers chiral? Explain. (d) The equilibrium constant for the formation of the cobalt(II) complex
produced by coordination of three oxalate anions, as in part (b), is 5.0 × 109. By comparison, the formation
constant for formation of the cobalt(II) complex with three molecules of ortho-phenanthroline (Table 24.2) is
9 × 1019.
From these results, what conclusions can you draw regarding the relative Lewis base properties of the two
ligands toward cobalt(II)? (e) Using the approach described in Sample Exercise 17.14, calculate the
concentration of free aqueous Co(II) ion in a solution initially containing 0.040 M oxalate ion and 0.0010 M
Co2+(aq) .
Solution
(a) The complex formed by coordination of one oxalate ion is octahedral:
Chemistry: The Central Science, Eleventh Edition
By Theodore E. Brown, H. Eugene LeMay, Bruce E. Bursten, and Catherine J. Murphy
With contributions from Patrick Woodward
Copyright ©2009 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Sample Integrative Exercise Putting Concepts Together
Solution (Continued)
(b) Because the oxalate ion has a charge of 2–, the net charge of a complex with three oxalate anions and
one Co2+ ion is 4–. Therefore, the coordination compound has the formula Na4[Co(C2O4)3].
(c) There is only one geometric isomer. The complex is chiral, however, in the same way as the [Co(en) 3]3+
complex, shown in Figure 24.20(b). These two mirror images are not superimposable, so there are two
enantiomers:
(d) The ortho-phenanthroline ligand is bidentate, like the oxalate ligand, so they both exhibit the chelate
effect. Thus, we can conclude that ortho-phenanthroline is a stronger Lewis base toward Co2+ than oxalate.
This conclusion is consistent with what we learned about bases in Section 16.7, namely that nitrogen bases
are generally stronger than oxygen bases. (Recall, for example, that NH 3 is a stronger base than H2O.)
Chemistry: The Central Science, Eleventh Edition
By Theodore E. Brown, H. Eugene LeMay, Bruce E. Bursten, and Catherine J. Murphy
With contributions from Patrick Woodward
Copyright ©2009 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Sample Integrative Exercise Putting Concepts Together
Solution (Continued)
(e) The equilibrium we must consider involves three moles of oxalate ion (represented as Ox 2– ).
The formation-constant expression is
Because Kf is so large, we can assume that essentially all of the Co 2+ is converted to the oxalato complex.
Under that assumption, the final concentration of [Co(Ox) 3]3– is 0.0010 M and that of oxalate ion is [Ox2–] =
(0.040) – 3(0.0010) = 0.037 M (three Ox2– ions react with each Co2+ ion).
We then have
Inserting these values into the equilibrium-constant expression, we have
Solving for x, we obtain 4 × 10-9 M. From this, we can see that the oxalate has complexed all but a tiny
fraction of the Co2+ present in solution.
Chemistry: The Central Science, Eleventh Edition
By Theodore E. Brown, H. Eugene LeMay, Bruce E. Bursten, and Catherine J. Murphy
With contributions from Patrick Woodward
Copyright ©2009 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.