* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Tunings and Temperaments Powerpoint
Survey
Document related concepts
Transcript
Tuning
• Intervals are based on relative pitches
– Works fine if you are a solo artist!
• Groups of musicians must tune to a
common reference pitch
– Concert A (440 Hz, maybe)
– Middle C
(used for pianos)
– Concert Bb (used for brass instruments)
• All other tunings are taken relative to
the agreed upon reference
Assigning Notes to Pitches
• We arbitrarily assign note names on a piano
using the letters A-G for the white keys
• By convention, the A above "Middle" C is
fixed at a frequency of 440 Hz
Middle
C D E F G A B C D E F G A B C
(440 Hz)
Brief History of 440 A
• No commonly agreed upon reference pitches before 1600
– Instruments often tuned to organ pipes of local churches
• In 1619, composer Michael Praetorius suggested 425 Hz
as a standard tuning (the so-called "chamber pitch")
– Higher tuning pitches not recommended, due to limited
construction techniques for stringed instruments
• In 1855, French physicist Jules Lissajous developed a
technique for calibrating tuning forks, suggested 435 Hz
as the standard pitch
– French government (under Napoleon) adopted 435 Hz in 1859
– Adopted internationally in 1885 at a conference in Vienna
Lissajous Patterns
• Lissajous's apparatus bounced a light
beam off mirrors attached to tuning forks
• Light produced patterns that could
determine relative frequencies of forks,
based on standard ratios for intervals
• The basic technique is still in use today!
History of 440 A, continued
• Industrial Age ( late 1800s) led to improvements in
metallurgy and construction techniques for instruments
– Concert pitch gradually started to creep up
• Present day 440 pitch adopted in US in 1939 (later by
ANSI)
• Modern orchestras (especially in Europe) now use 442
or even 445 as a reference pitch
• Note: this "history" is grossly over-simplified (we may
never know exactly how standard pitches evolved)
Modern Tuning Techniques
• Instruments today can be tuned electronically
(commercial tuning apparatus - stroboscopes,
etc) or acoustically (tuning forks)
• Monophonic instruments (i.e. most band
instruments) are tuned to a single reference, all
other pitches assumed to be "in tune"
• Polyphonic instruments (piano, guitar, most
orchestra instruments, bagpipes, etc) tune to
one reference, all other tunings derived relative
to that reference
Electronic Tuning Example
• An electronic tuner shows exactly what
pitch is being played and how far off it is
"Sharp" - pitch is too high
Just right!
"Flat" - pitch is too low
Acoustic Tuning
• Acoustic tuning is done by comparing the
instrument's pitch to a reference
• Pitches that are close to each other but out
of tune harmonically will "beat" at a
frequency equal to the difference between
the two frequencies being played
– Example: 442 vs 440 beats at 2 Hz
• Pitches that are not close will "beat" due to
interference in the upper harmonics (good
piano tuners use this characteristic)
Acoustic Tuning Example
• "Standard" tuning on a 6-string guitar is
E
A
D
G
B
E
Fourth Fourth Fourth
Third Fourth
• Tuning by "straight" frets
– Fourth == 5 frets, Third == 4 frets
• Tuning by harmonics
– Fourth == 5th
7th frets, Third == 9th
• As pitches get close, listen for "beats"
– No beats == pitches are in tune
5th frets
Why this Happens
• Consider two pitches an
octave apart
• Coincidental "zero
crossings" (shown by
arrows) eliminate "beats"
• Same effect with a Fifth
Out of Tune Pitches
• Two pitches a half step
apart (no crossings)
• Out of tune Fifth (2 cents
worth)
This all sounds very clinical
So how come piano tuners still have jobs?
Tuning "for real"
Proper tuning of a particular note on a particular
instrument is affected by many factors (some we
can control, some we cannot)
– Psychoacoustics
– Physical characteristics of the instrument (i.e.
how it is constructed)
– Overall temperament of the instrument (i.e.
how it is tuned)
Psychoacoustics
• Our ears process frequencies differently
depending on what register the notes are in
– Higher frequencies sound "flat"
– Lower frequencies sound "sharp"
• Professional piano tuners compensate for
this by tuning upper registers slightly sharp,
and lower registers slightly flat
– Differences can be as much as 20-30 cents
Intonation
• Intonation is how pitches are assigned or
determined relative to each other
– "Good" intonation means that all notes in all
positions are in tune, relatively speaking
– "Bad" intonation means that some notes are out of
tune
• Intonation can be adjusted!
– By the manufacturer ("setting up" a guitar)
– By the musician (adjusting the embouchure)
• Harmonic partials are almost always in tune problems are often encountered with chords
Temperament
(Who says scales are boring?)
• Temperament is how pitches are adjusted
relative to each other when an instrument
is tuned
• Temperament has a profound effect on
intonation
• It's impossible to get an instrument to be
truly "in tune"
– Temperaments have been confounding
musicians for almost 5000 years!
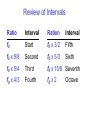
Review of Intervals
Ratio
Interval
Ration
Interval
f0
Start
f0 x 3/2
Fifth
f0 x 9/8
Second
f0 x 5/3
Sixth
f0 x 5/4
Third
f0 x 15/8 Seventh
f0 x 4/3
Fourth
f0 x 2
Octave
Now Assign Note Names
Name
Interval
Name
Interval
C
1/1
Start
G 3/2
Fifth
D
9/8
Second
A
5/3
Sixth
E
5/4
Third
B
15/8 Seventh
F
4/3
Fourth
C
2/1
Octave
Map onto Keys
C D E F G A B C
Taking the Fifth
Name
Interval
Name
Interval
C
1/1
Start
G 3/2
Fifth
D
9/8
Second
A
5/3
Sixth
E
5/4
Third
B
15/8 Seventh
F
4/3
Fourth
C
2/1
Octave
Corresponding notes in each row are perfect Fifths (C-G,
D-A, E-B, F-C), and should be separated by a ratio of 3/2
This one doesn't work!
A Little Music History
• Much of what we understand today about tuning and
temperament was discovered by the ancient Greeks
(specifically, Pythagoras and his followers)
– Harmonic Series, Intervals, etc
• One of the oldest tunings is the Pythagorean tuning,
which is based on the interval of the Fifth
• Tuning Factoid: the notes of any diatonic scale can be
rearranged in sequence such that the interval between
each consecutive note is a Fifth:
C
D
E
F
G
A
B
becomes:
F
C
G
D
A
E
B
Circle of Life, er, Fifths
By extending this idea (and utilizing both
black and white keys on a piano), it is
possible to start at any note, go up
twelve perfect Fifths, and end up at the
same note from whence you started (just
in a different octave)
We call this the Circle of Fifths; it is an important fundamental
concept that is the basis for much of modern music theory
You can even buy a wristwatch
whose face is a Circle of Fifths!
Back to Pythagoras
• The Pythagoreans based their tuning on Fourths and
Fifths, which were considered harmonically "pure":
C
Fourth
Fifth
F
G
Fifth
C
Fourth
• The Fourth was subdivided into two tones (whole step
interval), and a half tone (half step interval)
– This arrangement of intervals is called a tetrachord
– Two tetrachords can be concatenated together (separated by a
whole step) to create a diatonic scale
Tetrachords
C D E F G A B C
Tone
Tone
Half
Tone
Tetrachord
Tone
Tone
Half
Tetrachord
Diatonic
Pythagorean Tuning
Name
Interval
Name
Interval
C
1/1
Start
G
3/2
Fifth
D
9/8
Second
A
27/16 Sixth
E
81/64 Third
B
243/128
F
4/3
C
2/1
Fourth
Seventh
Octave
All whole step intervals are equal at 9/8 (204 cents)
All half step intervals are equal at 256/243 (90 cents)
Back to the Future
• Using the Circle of Fifths, we can start at any arbitrary
note at the "bottom" of the circle, and reach this note
again at the "top" of the circle (in a different octave) by
adding twelve perfect Fifths
– The "top" note will be 6 octaves above the bottom "note"
• We can then try to return to the original note by halving
the frequency of the "top" note six times
– Mathematically: (3/2)12 ÷ 26 == 531441/5524188 == 1.0136/1
– But this should be 1/1 because it's the same note!
• This difference between a note's frequency as
calculated via the Circle of Fifths versus its frequency
calculated via octaves is called a comma
Many Different Temperaments
•
•
•
•
Pythagorean Tuning
"Just" Tuning (four different modes!)
Mean-tone Tuning
Well-tempered Tuning
– J S Bach's Well-Tempered Clavier
• And of course …
– P D Q Bach's Short-Tempered Clavier
So how can we ever tune anything?
We get different results by tuning with different intervals!
Even Tempered Tuning
• Historically, different tunings and temperaments
have been used to improve the intonation of an
instrument
– Instruments sound "best" in only one "key"
– This is a problem if you want to transpose, or use
inharmonic intervals
• Starting in the 1850s, musicians began to use
"even" temperaments
– Much Classical and Romantic music required this, as
composers began to experiment with fuller, more
textured sounds and different key changes
– Makes it easier to tune pianos, harps, and organs
Even Temperament
• Even temperament divides an octave into
12 equally spaced half steps
– Every half step is always 100 cents
– Every whole step is always 200 cents
• Intervals are calculated based on
multiples of 21/12
– All intervals of like size will have the same
multiplier
– Some intervals may not "sound" in tune, but
we live with it to get more flexibility
What tuning should I use?
• In general, Even/Equal Temperaments
are easiest to deal with
• Some "period" pieces may sound better
in their original tunings
• Experiment with it and see what sounds
"best"!