Download Ch.3 lecture

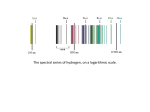
Chapter 3:
Spectral
lines in
stars
Emission and absorption of light
Continuous spectrum
(thermal, blackbody)
Independent of
composition
Emission line spectrum
Dependent on
composition
Each element has its own unique spectrum
Absorption lines in the Sun’s spectrum
Absorption Line Spectrum
QuickTime™ and a
TIFF (Uncompressed) decompressor
are needed to see this picture.
Gustav Kirchhoff (1824-1887)
absorption lines of hydrogen
Emission Line Spectrum
• Produced by a lowdensity gas
• depends on
composition and
temperature
Emission lines
The Balmer series for hydrogen: Visible light
electrons
falling to
n=2
Rydberg formula
(Balmer for nf = 2) :
1 /  = R (1/nf2 - 1/ni2)
R = Rydberg constant
= 1.097 x 107 m-1
The hydrogen atom
Energy levels and transitions of the many-electron atom: Sodium
Quantum states of the valence electron
The Bohr Model
•
•
Classical physics
predicts that the
electron should
spiral into the
nucleus
Cannot explain
emission spectra
The Bohr model:
•The e- stays in certain
stable orbits, emits no
radiation unless it jumps
to a lower level
•The angular momentum
of the e- is quantized
•the attaction between p
and e- provides the
centripetal acceleration
n = principal quantum number
From Coulomb’s law, the force between
the proton and electron is
1
F
=
40
q1 q2
r2
This is the centripetal force,
Where q1 = q2 = e for
the hydrogen atom
mv2 / r
So when the electron is in any energy level n:
Bohr radius a0 = 0h2 / me2 = 5.29 x 10-11 m
KE of the electron in the nth level: Kn = 1/2 mv2
PE of the electron in the nth level: Un =
-1
40
Total energy En = Kn + Un = ??? Compare to
Rydberg formula!
e2
r
Reduced mass: the nucleus is not infinite in mass, Bohr
model is off by 0.1%
m 1 m2
mr =
m 1 + m2
isotopes
Ionized Helium is also a 1-electron atom
Why is the emission spectrum of ionized helium
similar to that of hydrogen?
1. Because hydrogen and helium are similar
chemically
2. Because several of the energy levels of
hydrogen and helium are the same
3. Because hydrogen and helium have similar
atomic masses
4. It is a total coincidence
Energy Level Transitions
Not Allowed
Allowed
• Continuum
• Ionization
• Differences
between elements
• isotopes
Stellar classification scheme
QuickTime™ and a
TIFF (Uncompressed) decompressor
are needed to see this picture.
Is this star hotter or cooler than the Sun?
Spectrum of Arcturus
Luminosity
The
HertzsprungRussell diagram
plots the
luminosity vs.
temperature of
stars
Temperature
B - V is a measure of color: the smaller B-V, the hotter
the star (magnitudes, remember!)
Lines in a star’s spectrum correspond to a spectral type that reveals
its temperature
(Hottest)
O B A F G K M
(Coolest)