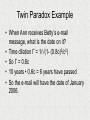* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download JKeehnLtalk
Modified Newtonian dynamics wikipedia , lookup
Specific impulse wikipedia , lookup
Classical central-force problem wikipedia , lookup
Sagnac effect wikipedia , lookup
Hunting oscillation wikipedia , lookup
Centripetal force wikipedia , lookup
Criticism of the theory of relativity wikipedia , lookup
Relational approach to quantum physics wikipedia , lookup
Fictitious force wikipedia , lookup
Equations of motion wikipedia , lookup
Seismometer wikipedia , lookup
Inertial frame of reference wikipedia , lookup
Relativistic mechanics wikipedia , lookup
One-way speed of light wikipedia , lookup
History of special relativity wikipedia , lookup
Frame of reference wikipedia , lookup
Classical mechanics wikipedia , lookup
Special relativity (alternative formulations) wikipedia , lookup
Derivations of the Lorentz transformations wikipedia , lookup
Minkowski diagram wikipedia , lookup
Twin paradox wikipedia , lookup
Special relativity wikipedia , lookup
Variable speed of light wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Length contraction wikipedia , lookup
Tests of special relativity wikipedia , lookup
Faster-than-light wikipedia , lookup
By: Jennifer Doran What was Known in 1900 • Newton’s laws of motion • Maxwell’s laws of electromagnetism Contradiction Between Laws Newton’s Laws Predicted that the speed of light should depend on the motion of the observer and the light source Maxwell’s Laws Predicted that light in a vacuum should travel at a constant speed regardless of the motion of the observer or source Two Postulates of Special Relativity • The laws of physics are the same for all non-accelerating observers • The speed of light in a vacuum is constant for all observers, regardless of motion Inconsistencies with Classical Mechanics • Newton’s Laws state that v+u=V • Einstein’s postulate says that the speed of light is independent of the motion of all observers and sources. Classical Lorentz Transformation x = x' + u t' ; y = y' ; z = z' ; t = t' OR x' = x – u t ; y = y' ; z = z' ; t = t' Then v = v' + u And a = a' BUT this is only good for u<<v. To make the transforms relativistic, assume: x = Γ (x' + u t') x' = Γ (x – u t) Finding Γ A light pulse starts at S at t = 0; S' at t' = 0 So in S, x = ct, and in S‘, x’ = c t', by Einstein’s second postulate Then ct = Γ (c t' + u t') = Γ (c + u) t' And ct' = Γ (c - u) t Substitute for t', then ct = [Γ(c + u)Γ(c - u)t]/c Then Γ2 = c2 / (c2-u2) = 1/(1- u2/c2) Γ = 1/√(1- u2/c2) Time Dilation • Δt = Γ•Δtp • Δtp is the proper time, the time between events which happen at the same place. • Since Γ is always greater than 1, all clocks run more slowly according to an observer in relative motion. Time Dilation Example • An astronaut in a spaceship traveling away from the earth at u = 0.6c decides to take a nap. He tells NASA that he will call them back in 1 hour. How long does his nap last as measured on earth? Time Dilation Example • • • • Δtp = 1 hour 1 – (u/v)2 = 1 – (0.6)2 = 0.64 Therefore, Γ = √(1/0.64) = 1.25 Δt = 1.25 hours Length Contraction • L = (1/Γ)•Lp • Lp is the length of the object in the reference frame in which the object is at rest. • All observers in motion relative to the object measure a shorter length, but only in the direction of motion. Length Contraction Length Contraction Example In the reference frame of a muon traveling at u = 0.999978c, what is the apparent thickness of the atmosphere? (To an observer on earth, the height of the atmosphere is 100 km.) Length Contraction Example • • • • L = (1/Γ)•Lp Lp = 100 km L = 100 km•√(1-(0.999978)2) L = 0.66 km = 660 m Relativistic Velocity Addition • When objects are moving at relativistic speeds, classical mechanics cannot be used. • v = (v' + u) / (1 + v'u/c2) • v = velocity addition • v' = velocity of object moving in the reference frame of u. • u = motion of object Relativistic Velocity Addition Example • A spaceship moving away from Earth at a speed of 0.80c fires a missile parallel to its direction of motion. The missile moves at a speed of 0.60c relative to the ship. What is the speed of the missile as measured by an observer on Earth? Relativistic Velocity Addition Example • • • • Cannot use classical mechanics. v is the velocity we are looking for. u = 0.80c = the velocity of the spaceship v' = 0.60c = the velocity of the missile in the reference frame of the spaceship • v = (v' + u) / (1 + v'u/c2) • v = (0.6c + 0.8c) / (1 + (0.6c)(0.8c)/c2) • v = 1.40c/1.48 = 0.95c Relativistic Velocity Addition Example • A star cruiser is moving away from the planet Mars with a speed of 0.58c and fires a rocket back towards the planet at a speed of 0.69c as seen from the star cruiser. What is the speed of the rocket as measured by an observer on the planet? Relativistic Velocity Addition Example • v is the velocity we are looking for. • u = 0.58c = the velocity of the spaceship • v' = -0.69c = the velocity of the rocket in the reference frame of the star cruiser • v = (v' + u) / (1 + v'u/c2) • v = (0.58c - 0.69c) / (1 + (0.58c)(0.69c)/c2) • v = -0.11c/0.5998 = -0.18c • Compared to –0.11c Twin Paradox • A clock in motion runs slower than one at rest, including biological clocks. • Apparent paradox with one twin staying on earth and other going on a relativistic journey. • Solution Twin Paradox Example • Twin sisters Betty and Ann decide to test the relativity theory. Ann stays on earth. On January 1, 2000, Betty goes off to a nearby dwarf star that is 8 light years from Earth. Betty travels there and back at 0.8c. Twin Paradox Example • What is Betty’s travel time to the star according to Ann? • t = d/v = 8 light years / 0.8c = 10 years • So Betty’s total travel time according to Ann is 20 years. Twin Paradox Example • As soon as Betty reaches the star, she sends her sister an e-mail message saying, “Wish you were here!” via radio. When, from Ann’s perspective, does Ann receive the e-mail from Betty? • 2010 + 8 yrs = 2018 Twin Paradox Example • When Ann receives Betty’s e-mail message, what is the date on it? • Time dilation Γ = 1/√(1- (0.8c)2/c2) • So Γ = 0.6c • 10 years • 0.6c = 6 years have passed • So the e-mail will have the date of January 2006. Twin Paradox Example • How much younger is Betty than Ann when Betty returns from the star? • For Betty, her return date is 2012, but for Ann, she returns in 2020. • Ann is now 8 years older than Betty. Twin Paradox Example Newtonian Gravity • Quote from Newton • Two masses in Newton’s theory — inertial mass and gravitational mass • Newton saw no reason why these masses should be equal • BUT they are!!! Einstein on Gravity “I was sitting in a chair in the patent office at Bern when all of a sudden a thought occurred to me: if a person falls freely he will not feel his own weight. This simple thought made a deep impression on me. It impelled me toward a theory of gravitation.” -Albert Einstein Principle of Equivalence • There is no local experiment that can be done to distinguish between the effects of a uniform gravitational field in a nonaccelerating inertial frame and the effects of a uniformly accelerating reference frame. Principle of Equivalence • Free space view is the same as the free fall view General Relativity • The presence of matter causes spacetime to warp or curve. • Gµv = 8G/c4•Tµv Schwarzschild’s Solution • Found the first exact solution of one of Einstein’s equations • The metric (distance relation) is: • ds2 = -c2(1-2MG/c2r)dt2 + dr2/(1-2MG/c2r) + r2(dq2+sin2qdf2). • Describes space-time geometry around a spherical object of mass M • Basis of tests of general relativity Testing the General Theory of Relativity • Deflection of Starlight • First tested during total solar eclipse in 1919 Slowing Down of Clocks by Gravity • Clock closer to the mass measures a shorter elapsed proper time than a clock that is further out. • Rc=2MG/c2, where Rc is the Schwarzschild radius.