* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lesson One
Electronic engineering wikipedia , lookup
Phase-locked loop wikipedia , lookup
Nanofluidic circuitry wikipedia , lookup
Integrated circuit wikipedia , lookup
Oscilloscope wikipedia , lookup
Analog television wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
Oscilloscope types wikipedia , lookup
Josephson voltage standard wikipedia , lookup
Index of electronics articles wikipedia , lookup
Integrating ADC wikipedia , lookup
Radio transmitter design wikipedia , lookup
Regenerative circuit wikipedia , lookup
Negative-feedback amplifier wikipedia , lookup
Oscilloscope history wikipedia , lookup
Valve audio amplifier technical specification wikipedia , lookup
Analog-to-digital converter wikipedia , lookup
Surge protector wikipedia , lookup
Transistor–transistor logic wikipedia , lookup
Voltage regulator wikipedia , lookup
Power electronics wikipedia , lookup
Current source wikipedia , lookup
Power MOSFET wikipedia , lookup
Two-port network wikipedia , lookup
Wilson current mirror wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Schmitt trigger wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Operational amplifier wikipedia , lookup
Rectiverter wikipedia , lookup
Network analysis (electrical circuits) wikipedia , lookup
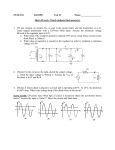
1 Key Lecture Concepts for EE 372 (Mostly Analog Electronics) by R.H.Cornely, Aug 24, 05 All Copyrights Reserved [Sentences in these notes that are enclosed in brackets contain information that may be interesting and important but can be left unread until the entire lesson is learned.] LESSON ONE: Introduction to Analog Electronics; Overall View of Electronics OVERVIEW AND OBJECTIVES: Lesson one presents an overview of the subject of circuits for analog signals and introduces most of the key concepts used in the course. It is expected that it will take several weeks of study before these concepts are mastered. Thus the parts of lesson one which are not understood should be read every three or four days until the lesson is mastered even while studying lessons 2, 3, and 4. The assigned problems and the solved examples in this lesson, and in all the lessons, should be practiced often and discussed in class to exercise the concepts. An analog signal usually represents a physical or chemical variable such as temperature, sound, electromagnetic waves (light), magnetism, and electrical current. The amplitudes of analog signals can have any value; i.e. they vary continuously or smoothly with time, e.g. as a sine wave, as opposed to the on/off, high/low values for digital signals. The variations can occur slowly as in the case of mechanical vibrations of a building or the temperature variations within a classroom. On the hand, analog circuits that can amplify very high frequency changes, in e.g. electromagnetic waves received by an antenna, are also required. In this information age, “very high frequency” refers to frequencies at gigahertz rates and higher. [Analog signals generally have time variations with different frequency components, e.g. representing e.g. the various sounds of musical instruments. Thus the frequency response of a hi-fidelity amplifier of analog signals is an important characteristic of amplifier of audio signals received from a sensor of sound, i.e. a microphone.] A sensor is a device that converts an input signal in the form of one type of energy (e.g. light) to an output signal in the form of another type of energy, e.g. voltage. [If the emphasis is on changing the energy form of the input (e.g. sound to current) the sensor is called a transducer. Examples of sensors that convert energy to electricity are solar cells and photodiodes (light to electricity), receiving antennas (e.g. radio waves to electrical signals), microphones (sound to electricity), and digital cameras (arrays of light detectors that convert patterns of incident light to patterns of charge that are moved on output lines to be digitized and stored in a memory chip).] Very soft musical sounds can be converted to current by a microphone and then amplified by electronic circuitry, i.e. an audio amplifier. To obtain loud sounds of the same music, the amplifier output voltage could be connected to a speaker. To record the sounds, a magnetic head device that converts the voltage to electromagnetic waves that magnetize a storage media, i.e. magnetic tape, can be used. As another example, the electromagnetic radiation sent out from the transmitters of astronauts needs to be selected from the radiation emitted by hot bodies as the sun and stars. Since the unwanted background radiation, or noise, has many frequencies (broad spectrum, the astronauts send their messages within a narrow frequency spectrum. The electronic amplifier on earth is designed to selectively amplify just those frequencies and not amplify the most of the frequencies of the background noise. An important focus of this course is how to design an electronic amplifier to control the selected frequencies that will be amplified (its frequency response) so the desired signals are amplified and unwanted signals (noise) attenuated. 1 2 The focus of this course is on small-signal analog circuits, i.e. sine wave signals whose small amplitude and frequency vary with time. The objective of this lesson is to introduce the key concepts for amplifying and shaping these signals. Small-signal analog circuits process information in the form of voltages that are typically less than 100 mV. These relatively tiny waveforms, or wiggles, are superimposed on top of DC voltages, of the order of volts. The DC voltages bias the operating point (called the Q point) of the transistors so that it is kept in a region of its I/V characteristic where the small signal output current is a linear function of the small signal input voltage. Thus small signal analog electronics is also called linear electronics. Recall that digital electronics is based on exploiting nonlinear characteristics such as the output versus input transfer curves of devices. Large-amplitude analog signals (e.g. signals with amplitudes greater than 100 mV) are discussed in the last lesson of this course. Their analysis is based on the transfer curve concept in the Electronics One course. An example of a large-amplitude analog signal is a ten volt sine wave sent from the output of an audio amplifier to a speaker system. This lesson introduces the bipolar junction transistor, BJT. The BJT consists basically of a forward biased diode whose current is injected into a nearby reversed biased diode. The diodes are both within the same piece of material that is the transistor structure. The BJT has some advantages and some disadvantages versus its four-decade competitor, the MOST. The output of both the MOST and BJT is in the form of small-signal current that is able to “drive”, or control, either another transistor or an external “load”, e.g. a speaker. The input to the transistor is a small-signal voltage. The load as a resistance converts the output current to an output voltage. (The output voltage of course depends on the amount of output current resulting from the input voltage. Thus the change in output current divided by its cause, the change in input voltage, is an important property which is named the transconductance. The transconductance is referred to as a figure of merit. Its value and dependence on DC bias current and device size have entered every discussion, or argument, in which MOST and BJT devices have been compared. To help remember this fundamental idea, note that conductance means current divided by voltage. The syllable “trans” indicates that the current and voltage are at two different locations or “on the other side of” as “transatlantic” or “translation”. An important objective of this course and lesson is to show how small signal transistor circuit models for the BJT and MOST are used in the analysis and design of analog circuits. These linear circuit models replace the transistors by resistors and dependent current sources, which depend on the transconductance, so that linear circuit theory can be applied. A final section of this long lesson focuses on the junction field effect transistor, JFET. This knowledge is needed to prepare for experiments in the EE 392 Laboratory Course. The 392 course is often taken concurrently with EE 372. 2 3 A) Comparison of the Different Types of Electronic Circuits There are four types of signals used in electronic circuits. They are Digital (DS), Small Signal Analog (SSA), Large Signal Analog (LSA), and Mixed (MS). Pictorial representations of the four types are shown in fig1. The amplitudes of the sketched waveforms have typical values. Digital electronic circuits manipulate signals that have discrete amplitude levels, e.g. 0 and 3 volts. Digital circuit design involves finding clever ways to use three terminal devices with nonlinear characteristics, particularly the MOSFET, to perform digital logic and storage by quickly charging and discharging capacitance. The capacitance is often parasitic (undesired); however, sometimes capacitors are deliberately introduced, e.g. for charge storage elements for memory. This topic, covered in Electronics One, will be studied again in the third electronics course with the active MOSFET component replaced by other electronic systems composed of integrated circuits. Analog electronic circuits have voltage and current waveforms that are not discrete but are varying continuously (smoothly) with time. An input waveform, or signal, can have all possible amplitudes. The amplitudes are proportional to the physical variables that they represent. Examples of such variables are fluid flow rates, the sounds of an orchestra, light intensity, magnetic forces, and temperature. An example of a large signal analog waveform is shown in the upper right corner of fig1.1. The voltage waveform might represent the temperature in a room that is varying between 70 and 62 degrees with the time scale in hours and the voltage varying either about zero volts or about some DC value corresponding to an average temperature. The amplitudes of the waveforms, as the variables they represent, can vary with time continuously between positive and negative maximum values. Thus the analog signals can have any value within a continuous range. Usually the frequency of the total, or actual, signal is varying with time as in the case of the large and small signal analog waveforms in fig1.1. The signal generally is made up of sine waves with different frequencies and amplitudes that are summed together, or superimposed, to give the total signal. Analog circuits often are required to amplify the total signal without changing its frequency content, i.e. the relative amplitudes of the sine waves of different frequencies that make up the actual signal. Thus all the signals with different frequencies have to be amplified by the same amount. This is particularly challenging if the signal to be amplified has significant frequency components in the gigahertz range required by broadband communications systems. Therefore the designers of amplifiers of analog signals must be concerned with how the amplification varies with frequency. This is called the frequency response of the amplifier. In this course the analog circuits will be discussed and analyzed as if the input signal representing a physical variable had a single frequency. The total response of an analog amplifier to an actual input signal is obtained from the output responses to the different frequency signals that make up the actual input signal. For analysis, the calculated responses to input signals with different frequencies can be superimposed, or added together. If the amplitudes of the signals are "small enough”, the transistors in the analog circuit that amplify the total signal can be represented by linear circuit models. An example of a small analog signal is the signal shown in the lower left corner of fig1.1. It looks as if it is a small wiggle of the order of 1.0 [mV] riding on top of 1.0 volt DC. 3 4 For input signals with “small” amplitudes, a linear transistor model can approximate the nonlinear three terminal device characteristics. The model consists of linear resistors and dependent current sources. Examples of the small signal circuit models and symbols for the two types of transistors used in analog circuits, MOST and BJT, are shown in fig1.2. [Capacitors must be added to the model, as shown, if the signal frequencies are high enough to cause time delays between the output and input. Note the capacitors dotted into the BJT and MOST models.] The analog circuits can be analyzed when the input signal is “small” by replacing each of the actual transistors in the analog circuits by its small signal circuit model and performing circuit analysis as done in the Circuits One course. [However, a more effective approach will be taught in this course that will simplify analog circuit analysis and design particularly when the circuit has more than two or three transistors.] The values for the resistors and other parameters for the components in the small signal circuit will depend on the DC voltages and DC currents of the 3-terminal transistors. Approximately one third of the analytical work in this course will be DC analysis of MOST and BJT circuits. The purpose of the DC voltages, or currents, is to bias the transistors so that they operate at a Q point on the device characteristic. The Q point should be located where the transconductance has its highest value and required output current variations with time are not distorted with respect to the shape of the input waveform. [Do you recall finding the Q points for diodes and MOS transistors in Electronics One using DC linear models? A battery and resistor to approximate the nonlinear diode curve were used.] To effectively amplify the ac input current or voltage, a three-terminal device must be properly biased into a region that can produce an output that is linearly proportional to the input signal. Large signal circuit analysis is required when the amplitude of the input signals are large enough that the small signal circuit models do not accurately predict the circuit behavior. In Electronics One you learned how to use DC models for two terminal nonlinear diodes and to use voltage transfer characteristics to relate output voltages to input voltages. The techniques for analysis of circuits with large signals are similar to these and will be discussed in the last lesson of the course. A fourth type of electronic circuit is one that converts analog signals to digital, or vice versa. These circuits could be called mixed. An example of a possible waveform in such a circuit is shown in the lower right of fig1.1. Note that discrete voltage levels are superimposed on top of an analog signal. An example of a mixed circuit is the computer modems that convert analog telephone signals to the digital signals used in the computer. These circuits, not covered in Electronics Two, can be understood using the basic concepts for the other three types of circuits. B) Small Signal Linear Models for Representing Nonlinear Devices To introduce the concept of small signal circuit models, we will first study the diode and then the closely related three-terminal device, the bipolar transistor. The graphs and equations in fig1.3 summarize how the nonlinear diode can be treated as a linear resistor for analog signal waveforms with small amplitude. The diode equation for the characteristic in fig1.3a is the familiar equation 1 at the bottom of the figure. 4 5 The diode voltage will normally have two components: a DC voltage that has the symbol VD (which biases the device, or puts the Q point at a desired location on the I/V characteristic) and a small, time varying voltage, vd, the analog signal. This small signal input could be a voltage of amplitude vd that varies sinusoidally with time. The "output", or the response to the input, is the current which also has a DC component, ID, plus an ac component id, with the symbol for their sum being iD. Please adopt the habit of writing upper case letters and subscripts if a symbol is for DC currents or voltages and lower case letters and subscripts for ac currents or voltages. For total voltage or current values (DC plus ac components) use a combination of lower and upper case letters as shown under fig1.3a. In fig1.3b the portion of the curve involving the input signal is magnified and the region around the DC bias point, or Q point, corresponding to VD and ID, is enlarged. The total current at each instant of time can be obtained graphically by reflecting each input value off the characteristic curve at times t1, t2 , t3, etc. to obtain the current waveform, as shown in fig1.3c. Again, the value of current at each moment of time (t1, t2, t3 etc.) can be found by extending a line from each value of input voltage (for each moment) upwards and reflecting the line off either the actual diode curve, as in fig1.3c. This method is also applied in fig1.3d but the linear approximation rather than the diode curve is used. From the difference in the outputs, for the two different reflections, one can appreciate how the distortion of the output current would become worse as the input voltage becomes larger. (Distortion refers to the output current not having the same shape as the input voltage.) The graphical analysis is more easily done with triangle versus sinusoidal inputs, as in fig1.3e and the exercise below. Exercise 1.1 Refer to fig1.11. Complete the sketch of the output current for the two triangular input voltages by reflecting the input voltage off the nonlinear diode curve, not its tangent. Note that there is much more distortion for the large amplitude input because the reflections are from the part of the diode curve that has more curvature. Refer to fig1.3c. Note that if the ac voltage signal is zero, the output current is simply the DC current ID. Note also that because the sine wave voltage input is "large", the current waveform is not a sine wave because the diode characteristic is nonlinear. If the ac voltage, vd, is small enough, the nonlinear curve can be taken to be a straight line tangent to the curve in the neighborhood of the Q pt. as shown in fig1.3d. There will be no significant error, or difference between the current waveform reflected from the actual curve versus the straight line, the approximation of the curve, if the signal is "small". The sine wave component of the voltage applied to the diode will cause a current id that will also be a sine wave, with the same frequency as the ac component of the “input” voltage. The amplitude of the current will be proportional to the small signal conductance, which is the slope of the diode curve. [If the curve is steep, the resistance will be smaller and there will be more ac current.] Fig1.3e shows that the reflection method can be applied to any arbitrarily shaped signal. An important result is given in equation 3 at the bottom of fig1.3. It is derived by differentiation of equation 1, as shown by equation 2. It follows as shown by equation 3 that the ac conductance of the diode is proportional to the DC current divided by the thermal voltage times the ideality factor, n. [This assumes the normal condition of ID being much greater than the reverse saturation current, IS.] 5 6 The key result to memorize is that the diode resistance is inversely proportional to ID, as shown in equation 1 below. Thus the DC Q pt. parameter, ID, controls the "voltage to current conversion gain" of the device. 1) = 3a) r = vd / id = nVT / ID r 25 mV / ID [mA] (assuming nVT = 0.025 V = 25 mV) For convenience in this course 25 mV always will be taken as the value of the thermal voltage times the ideality factor, although actually it is a variable that depends on the ambient temperature. Equation 1 is used often to connect the DC world to the ac world. Figs1.3c, d, and e show that during the time when the total input voltage is greater than the DC voltage the total output current is greater than the DC diode current. When the voltage is less than VD, the output current will be less than the DC current. The small signal current adds to and then subtracts from the DC bias current as time varies, i.e. the signal current flows into the anode when the ac diode voltage is positive and away from the anode when the ac voltage is negative. The ac voltage and current are said to be in phase since when one waveform is positive the other is positive. If they were out of phase they would have opposite polarities at the same time. The concept of phase is very important in analog electronics. In small signal analysis and design, it is convenient to use superposition theory and work either with the DC currents and voltages or with the ac voltages and currents, but never at the same time. Thus for an analysis problem, we will put on our “DC hat” first and do a DC analysis. Then we will put on our “ac hat” and do ac analysis to find the result we seek. [Have you ever notice anyone wearing two hats at the same time? Do they appear to be able to able to accomplish anything?] Thus there is a need to have an ac model for the diode as well as the DC diode models that were used in digital electronics. Based on the previous discussion, the ac model for a pn junction is simply a resistor, as shown in fig1.4. Also shown is one familiar DC model. [In this course the value for the DC voltage for the battery will be chosen to be either 0.6 or 0.7 [v], although any value between 0.3 and 1.4 [v] could be a reasonable choice, depending on the diode, its material and structure, the biasing current and the temperature. The resistance in series with the battery is often very small compared to the external biasing resistors; thus it will be usually neglected in this course.] For the FET and BJT three terminal devices, an input ac voltage will be applied across two “input” terminals and the resultant small signal current from a third terminal is the “output”. The ratio of the output current variation, or wiggle, to the input voltage wiggle is defined as the transconductance. This is THE MOST IMPORTANT PROPERTY of any three terminal electronic device. As stated earlier, the syllable "trans" is added to the word conductance because the voltage is applied to one terminal and the output current is taken from a different location or terminal, unlike the diode. C) The Bipolar Transistor (BJT), Two Closely Coupled Diodes Fig1.5 introduces the BJT and its DC and ac circuit models. Observe carefully the symbol and structure for the NPN and the PNP bipolar junction transistor shown in fig1.5a. The BJT consists of 3 semiconductor regions: emitter (E), base (B), and collector (C); observe that there are two PN junctions. 6 7 For an NPN BJT the emitter can be considered as a source of electrons that “throws” them at the collector. The emitter region is much more heavily doped with impurities added to the host silicon atoms than the collector region. This causes an electron enrichment of the E region as indicated by the plus sign next to the N in the structure. The base terminal has the role of enabling forward bias voltage to be applied between the base and emitter diode. This voltage causes the injection of electrons from the emitter that flow towards the collector, passing through the thin P-type base region. The base region is kept thin to enable the electrons to pass quickly through the region before they have a chance to recombine with the holes of the P region. [The oppositely charged carriers attract each other and recombine if they are given enough time. This time to recombine is called the recombination time, or just lifetime. With the mobility parameter, it is the most important property of semiconductor material. Thus the thickness and doping level of the base region controls the electron current flow through the reversed biased collector-base diode to the collector terminal.] As described above, the base region unfortunately tends to capture a small percentage of the electrons flowing from the emitter to the collector. Thus the collector current always will be slightly less than the emitter current. The transistor is designed so that the base region is as thin as possible to reduce hole flow from the metal contact into the base to make up for the holes that are “grabbed” by the oppositely charged electrons. [Holes most flow into the base to maintain total charge neutrality, summation of all charges equal to zero. In modern transistors the base region is as thin as 0.1 microns or less, i.e. about 300 atomic layers. For PNP transistors, the function of the emitter is to shoot positively charged, mobile holes towards the collector in response to forward bias between the base and emitter diode.] The BJT can be modeled for normal operation by a diode between the B and E terminals and a dependent current source between the C and B terminals, as shown for the NPN and PNP in fig1.5b. [Normal bias is when the EB junction is forward biased and the CB junction reversed biased.] The value of the dependent current source is the DC Beta times the base current IB, or equivalently DC Alpha times the emitter current IE. [Alpha, , and Beta, , are related by equations shown at the right-hand margin in fig1.5b. They are usually given convenient values in this course of 0.99 and 99.] The current directions when the emitter-base junction is forward biased are shown in fig1.5b. The value of Beta can be more than 1000 or as small as 30. Thus the base current is normally very small and IC only a slightly smaller than IE. Exercise 1.2 Derive the equations shown at the right-hand side of fig1.5b. They are useful to find alpha when beta is given and vice versa. The base-emitter diode current is the emitter current, IE. For both the PNP and NPN, IE = IB + IC. Hint: Use ≡ IC /IE and ≡ IC / IB When both junctions are reversed biased, the transistor is biased in the cutoff region and all currents are ideally zero, although actually small leakage currents related to the diodes reverse saturation current and the transistor's Beta actually exist. Although there are four possible bias regions, saturation and reverse active being the names for the other two, analog circuit operation requires that the transistor be biased in the active only. [Four corresponds to the four possible biasing combinations for the base-collector and base-emitter junctions. Each quadrant of the BIAS SPACE plot, fig1.5d, is for different possible combinations of forward and reverse bias for the BC and BE junctions. 7 8 In the cutoff region, the base-collector and base-emitter diode junctions are both reversed biased, as indicated by the signs of the voltages applied to the junctions. In the saturation region, both junctions are forward biased. When designing the bias circuit for non-distorted amplification of small signals, these regions are to be avoided under all operating conditions.] Note the useful equations in the table under fig1.5d with equations useful for relating the three BJT currents. Exercise 1.3 (optional). Construct a Bias Space figure for a PNP transistor. D) DC Analysis of BJT Circuits The objective of DC analysis is to find the Q point values for the BJT: that is the values for either IC or IE and for either VCE (if the transistor is a NPN) or VEC (if the transistor is a PNP). [The Q point values are needed because the values of ac parameters in the transistor models depend on the DC biasing of the transistors, i.e. the Q points.] The analysis can be done in three steps as presented in the text at the left of the first example in fig1.6. As you read each step, refer to the equations in example 1 (for a PNP) at the right of the steps. As previously explained, for convenience the value for eta is taken to be 99, although modern BJT transistors have values up to 10,000, or more. A reasonable value of 0.6 [v] for VBE (and for VEB for a PNP) are assumed for the examples. [Actually the diode voltage depends on the diode current, IE. However, in this course we will not take the time to find the exact value as was done in Electronics One. The diode equation for the diode voltage as a function of current shows that for various practical emitter current values the emitter-base voltage will usually between 0.5 and 0.8.] [Recall from figs1.5b and 1.5d that = /(1+ )]. Step 3 is a necessary check to see if the voltage between the collector and the base is such that the collector base junction is reversed-biased. If it is, then the Q point values are correct. If it is forward biased by more than about 0.4 volts, current will be injected from the base into the collector independent that is in the opposite direction of the normal collector current. The collector current will not equal Beta times the base current but will be less. The transistor is said to be in the saturation region and a saturation model for the BJT would be used to find the Q point. However, further analysis is not necessary in this analog electronics course since the transistors must be biased in the active region for normal applications. [For future reference after this course, bias space sketches summarizing the four possible regions of PNP and NPN transistors is given on the third page of figure 6. The use of the equations relating beta and alpha assumed that the BJT was in the active region. If the method given is used the voltage drops will always be positive values unless the transistor is incorrectly biased into the saturation region. The homework drill exercises will have some transistors biased into the cutoff and saturation regions to exercise your understanding.] Three other examples of how to find the Q point values for a BJT circuits are given on page 2 of fig1.6. The solutions for the examples should be studied and then practiced without referring to the solutions. For example 2 note that the first equation can be immediately written in the form of equation 1a, since the value of the emitter current is sought. [Note that if there are two or more resistors in the base biasing circuit, the Thevinin equivalent theory can be used to reduce the circuit to a single resistor and a modified base supply voltage. This will be done later in the course.] 8 9 Exercise 1.4 Study again the four examples of Q point analysis in the class handout and then do the assigned drill problems for PNP and NPN transistors. These problems will be handed out in class. If your analysis shows that the junctions are both reversed biased, it should be noted that the BJT is incorrectly biased in the cutoff region and no further work needs to be done. Similarly, if both junctions are forward biased, it should be noted that the transistor is incorrectly biased in the saturation region and no further work done. E) Introduction to Small Signal Analysis of BJT Circuits Small-signal ac analysis is done without concern for DC voltages and currents by using superposition, just as explained for the diode in section B. First the DC currents and voltages for the BJT are found by DC analysis, to determine the parameters in the ac circuit model for the BJT. Then the ac analysis is done using the circuit models in fig1.5c. Looking at the ac models in fig1.5c, note that the models for the PNP and NPN transistors are the same. The direction of the arrow of the dependent current source depends only on the polarity (phase) of the voltage across the BE junction and not on whether the BJT is a PNP or NPN. This is because the B-E junction is modeled as a resistor and the directional property of the diode is no longer a factor. When the ac voltage at the base relative to the emitter is positive (as indicated by the + sign on the base and the negative sign on the emitter), the current increases in the direction of base to emitter. As a result the collector to base current increases as indicated by the arrow next to the ac symbol for collector current. On the other hand, as the voltage at the base relative to the emitter decreases, as indicated by the positive polarity of the voltage between the emitter and base, the ac current flows from the base towards the collector. Understanding this phase relation is very important. Fig1.7 is designed to help you understand the concept of superposition of the DC and ac analyses. Study this figure carefully. Also review fig1.8 which shows the ac model drawn in the shape of the letter T. Note that this circuit model for the transistor is identical to the model in fig1.5c; however, it is twisted into a letter T shape so that it is easier to see that the vbe voltage is the input and the dependent current source is the resultant output. This output current can be pushed through a load resistor to provide an output voltage that can be much larger than the input voltage. Thus the transistor can provide a voltage gain; that is, the ac voltage across the load resistor, the output signal, can be much greater than the voltage input signal across the base emitter junction, re. [Please note again that capital letters for the current and voltage symbols and subscripts are used for DC, while lower case letters are used for ac.] F) Examples of Analog Circuit Analysis The voltage gain and input impedance for a simplified BJT circuit will be found in the first example. The BJT circuit, in fig1.9a, has only an ac input vIN. The DC bias circuitry is left out to simplify the circuit. The first step in the analysis of this circuit is to redraw the circuit by replacing the BJT component with its “T” circuit model as done in fig1.9b. The “T” circuit model is drawn first and then the components attached to the e, b, and c terminals in fig1.9a are connected between the corresponding terminals of the model in fig1.9b and the rest of the circuit. For this simplified circuit example the only component to attach is the 10K resistor to VCC. Note that in fig1.9b the resistor was placed between the collector terminal and ground and not a DC voltage. VCC was replaced by ground, since DC voltages are shorts for ac signals. 9 10 If the voltage on one side of a battery, or power supply, is increased by some value, the voltage on the other side is increased by the same amount, as shown in the insert at the right of circuit in fig1.9b. [Please remember that DC voltages are shorts in the “ac world” and DC current sources are open circuits.] In the analysis under the circuit in fig1.9b the input impedance, Zin, which is defined as the input voltage vin divided by input current, iin, is found by setting the input voltage equal to the IR drop across the ac emitter junction resistance, re. Note that the current flowing through this resistance is more than the input current! The result is that the resistance of the base emitter diode, re, is effectively increased by ( + 1). [The changing of the apparent value of impedance between two terminals by transistors is a key concept in analog electronics. Once the application of this concept is mastered, the analysis and design of circuits with more than one transistor can be easily done without redrawing the original circuit, as was done in fig1.9b.] The voltage “gain”, v0/vin, is found by the analysis initiated by equations 2a and 2b. Please practice finding the voltage gain (− 400) by copying the circuit in fig1.9a on a sheet of paper and repeating the work done in fig1.9b. Also please study the time, or phase, relationship of the output and input voltages in the Phase Analysis under the circuit and note the resulting out-of-phase relationship of the waveforms in fig1.9c. The example in fig1.10 presents an overview of the key concepts and techniques that are used to analyze analog circuits. For simplification purposes it is assumed that DC analysis has been done previously and that the DC emitter base diode current, IE, was found to be 1 mA. [The DC analysis would be done as in the problems in exercise 1.4 by using the circuit with the DC biasing voltages VBB and VCC and the 2.5 M base biasing resistor connected to the base-emitter diode.] The role of the capacitor is to isolate, or protect, the ac input source from the DC voltage at the base. Note again that since DC voltages are shorts for ac signals, the biasing voltages can be replaced by ground for ac signals. As previously mentioned, the DC and ac Betas were given as 99, a convenient value to work with. [Normally ac and DC beta values for a BJT are e.g.10% different when the device characteristics are measured; however, in many textbooks, such as Jaeger and Blaylock, the DC and ac beta values are taken to be equal] The emitter base diode resistance is calculated to be 25 ohms. Multiplying that value by +1 (i.e. 100), the input impedance between the base and emitter junction is found to be 2.5 K. That value is then put into a box on the circuit diagram, with an arrow pointing in the direction of the base. The box is used to highlight this important and useful result. All the circuitry to the right of that box can be treated as a resistor of 2.5Kattached from the base to ground. Understanding and applying this concept is a crucial for analysis of more complicated circuits. If there are any questions about the concept please bring them to the attention of the instructor and exercise the ideas in discussions with classmates and instructor during the class. The steps a, b, and c in fig10b are done after the input impedance is found and put in the box. They are the critical first steps to find the voltage gain of the circuit. After they are done it is straight-forward to write equations for the base and collector currents, ib and ic, as done in equations 1 and 2. The output voltage and input voltages can then both be written in terms of the base current, as in equations 3 and 1a and the voltage gain, Av, found as shown in the lower left corner of the figure. 10 11 To obtain a quick and reasonable result, the 2.5M resistance to ground was neglected compared with the 25K input resistance. Thus two of the three parameters of interest for any small signal amplifier (the input impedance, the voltage gain and the output impedance) have been found. Note the 180 degree shift, phase relationship, in the plots of the input and output voltages. [The analysis at the lower right side shows that neglecting the shunting of input current by the 2.5Mresistor has little effect on the voltage gain. However, the current division approach accounting for this shunt to ground effect will be important in other problems. The importance of input and output impedance in analog electronics cannot be overemphasized; it will be taken up in more detail in lesson 2 and used in each of the remaining hours of the course! Exercise 1.5 Draw the circuit at the top of fig1.10 on a sheet of paper. Without looking at the solution in the figure, find the voltage gain and compare your answer with the value of – 283. Sketch the output waveform for a sinusoidal input of five microvolts. Exercise 1.6 You speak into a microphone at a radio studio. Your friend tells you a week later what he heard and you smile. What different forms of energy related to the voice signal occurred during this week? G) The Basic Model for an Amplifier and Examples of Limits on its Effectiveness A small signal amplifier can be modeled in terms of its input and output impedance and its voltage gain, as shown by the model circuit in the amplifier “box” in fig1.12a. Example values for the input impedance, RI, and output impedance, R0, and the voltage gain, AV, are given in parentheses. Note that the impedances of the amplifier are fixed, and modeled as internal or “in the box”. This amplifier may not be necessarily effective for the loads it may have to drive and for the signal sources driving it as shown by the examples. In the example problems in fig1.12b the amplifier, with the given values, is driven by signal sources with different values for the signal source impedance and with various loads attached to the output of the amplifier. The examples are designed to show how the overall signal gain, v0/vS, depends on not only the voltage gain of the amplifier, AV, but on the ratio of the amplifier input impedance to the sum of the input impedance plus the signal source impedance. The gain also depends on the ratio of the load resistance to the sum of the load resistance and amplifier output resistance. Exercise 1.7 Practice the examples given in fig1.12b and do problems presented without solutions in class. Can you answer the question in fig1.12b? Explain all the critical factors to achieve large overall gain in an amplifier circuit. H) The Junction Field Effect Transistor Fig 1.13 summarizes the JFET device characteristics, as done for the four different MOS transistors in the notes for Electronics One. The characteristics of the device are basically the same as the depletion mode MOST (DMOS) except that the n-channel device can not be operated with the gate to source voltage more than a small positive voltage or the gate draws significant current. 11 12 [This results in the loss of the isolation between the gate and the source, critical for the field effect device to function.] From the drain characteristic it is seen that as for the DMOST there is a linear region where the device acts as a voltage controlled resistor, with VGS the voltage that changes the resistance. There is also a saturation region, or constant current region. If the Q point is in that region, the device acts as a “constant” current source with a current value largely independent of the drain to source voltage. The current in the saturation region can be changed by changing the gate to source voltage, as shown by the transfer characteristic. [The physical operation of the device is based on the widening of the depletion region of a reversed biased diode which effectively changes the resistance between the drain and the source, and thus the current for a fixed drain to source voltage. The physical operation is entirely different than that for the MOST, which is based on changing the carrier concentration, thus the conductivity and source to drain resistance, of the electrons which carry the current between the source and the drain.] The equation for the JFET saturation region, equation 1, has the same form as the equation for the MOST. Thus if K for the DMOS equations is replaced by (2IDSS)/(VP)2, where IDSS is two times the saturation current for VGS = 0, equation 1 is obtained. The threshold voltage for a DMOS corresponds to the pinchoff voltage, VP, for a JFET. Thus the values for RON and gm can be found from values for the pinchoff voltage and IDSS from measured characteristics on a curve tracer similar to the curves in the upper right of the figure. The equations for the JFET and MOST in the saturation and linear regions are given and compared in the figure for your convenience. For small signal inputs the JFET if biased in its linear region can be replaced by RON = r. If it is the saturation region, the device can be represented by the model for the MOST shown in fig1.2, with the capacitors replaced by open circuits if the signal frequency is relatively small. I) Summary You have achieved a reasonable mastery of this lesson when you can understand and solve on your own the examples in figs1.10, 1.11 and 1.12 and can do the BJT DC analysis exercises, similar to the examples in fig1.6. DC analysis of MOST circuits was studied in the Electronics One course and will be reviewed and used in later lessons. 12 13 Fig. 1.1 Examples of the Four Types of Electronic Signals Fig.l.2 Examples of Small Signal Models 13 14 Fig. 1.3 Small Signal Modeling of the Diode Distorted a output iD sine wave input, v D 1 iD ISe VD nVT -IS 2 δi D δv D I S e vD nVT nVT I D +IS nVT =g d Ideality factor, n: 1<n<2; Thermanl voltage, VT : VT k T q ; nVT 25mV Therefore, 3 g d I D nVT I D mA 25 mV or 3a rd 25 mV I D mA 14 15 Fig. 1.4 DC and ac Circuit Models for the Diode Input: vd VD vd Output: i D I D id Input: vD VD vd Output: i D I D id 15 16 Fig. 1.5 Symbols and a.c. Models for NPN and PNP Bipolar Transistors a) Structures and Symbols for NPN and PNP Transistors α IC IE β ICB I Transistor circuits are analyzed at one instant of time and usually the "arrow down" model is used unless the circuit has more than one transistor. 16 17 Fig. 1.5d Bias Space for an NPN BJT Transistor Exercise 1.3 Complete the construction of a bias space figure for a PNP Bipolar Transistor. Label the axes as shown. Hint: when VEB and VCB are both positive, both junctions are forward biased and, the BJT would be in its saturation mode. Table 1.5 Useful Equations for Relating I B , IC , and I E . 17 18 Figl.6 Finding the Q Point of BJT Circuits; General Procedure and Three Examples Procedure: The Q Point is determined by finding either I C or I E along with VCE (for an NPN transistor) or VEC (for a PNP transistor). The following steps should, be taken to find the Q point: 1) Write a loop equation for the base emitter loop by assuming a reasonable value for base emitter diode voltage drop. (A reasonable value would be 0.4 to 0.75 [v].) For this course 0.6 [v]will normally be assumed. Set the total voltage applied to the base emitter loop equal to VBE (or VEB for a PNP) plus the sum of the IR drops across the resistors in the base and emitter circuits. (Assume the convenient value for of 99.) Write the base current as the emitter current divided by plus 1 when you first write the equation to save time. Solve for the emitter current, I E (The collector current can be found if needed by multiplying I E by a, i.e. 0.99 for 99 . The base current can be found if needed by dividing the emitter current by 1 .) ~ 2) Find VCE ,or VEC ,by writing a loop equation for the loop from the collector supply voltage to the emitter supply voltage. Set the total voltage applied to this loop equal to the IR drops plus VCE ,or VEC ,and solve for VCE ,or VEC . (To save time express the IR drop for the collector resistor in terms of the known value of I E by using IC 0.99I E ). 3) Steps 1 and 2 were done by assuming that the BJT was in the active mode and therefore that I c I B . This assumption has to be checked, after the value for the collector to emitter voltage is found, by seeing if the collector to base junction is reversed biased or if forward biased has less than 0.3 volts so that the diode current of the junction is negligible. An easy way to do this is to make sure that VCE is positive for an NPN and greater than about 0.3 [v] and that VEC is positive for a PNP and also greater than about 0.3 volts. If the voltage from the C to E is 0.3[v] for and NPN, the voltage from B to C would be 0.3 [v], since the voltage from B to E was taken to be 0.6[v]. (Check this statement by making certain that the summation of voltages around the transistor loop is the equal to zero.) 18 19 Example One 1 30.6 0.6 I E 1K IE 50 K 100 30 20 mA 1K 0.5 K 2 50 I E 1K VEC 0.99 I E 1a I E 2a VCE 50 I E 1K 0.99 = 50 20 19.8 10.2 V VE 10 I E 1K 10 V VB 10 VEB 10.6 V VC 40 0.99 I E 1K 20.2 V 19.8 VCB 20.2 10.6 9.6 V VCB 9.6 R biased 19 20 Fig 1.6 Continued THREE EXAMPLES Example Two BE loop:1 30.6 0.6 IE 50 K I E 1K 1 100 30 20 mA 1.5 K CE loop:2 40 0.99 I E 1K VCE I E 1k 1a I E 2a VCE 40 19.8 20 0.2 V VE 0 20 mA 1K 20 V VB VE 0.6 VC VE 0.2 20.2 V VBC 20.6 20.2 0.4 V VBC 0.4 V indicates BC junction is F-biased by 0.4 V and the junction is "almost" conducting BJT is at the edge of saturation. Assumption of BJT being active is "just" OK. 0.2 20 21 Example Three IE 30 50 K I E 1K I E 20 mA 100 1.5K 2 35 0.99 I E 1K VEC I E 1K VCE 4.98 V 1 30.6 0.6 VC 35 19.8 15.7 VB 20 0.6 20.6 VBC 4.9 VBC 4.9 indicates both BE and BC junctions are F-biased and BJT is saturated and 99 VBE 0.75, VCE 0.2 Example Four 300 K BE loop: 4.1 0.6 I E 0.5 K I E 1 mA 100 EC loop: 15.4 1 mA VEC 0.99*1 mA *10 K VEC 15.4 0.5 9.9 5 V VC 13.4 9.9 3.5 VE 2 0.5 1.5 V VB 1.5 0.6 0.9 V VBC 0.9 3.5 4.4 and jct. R-biased. OK BC junction R-biased means BJT is in active region 21 22 Fig 1.6c Bias Space for a PNP and an NPN Transistor 22 23 Fig. 1.7 Total Base-Emitter Voltage Waveform Decomposed Into Its DC and ac Components. Fig. 1.8 The ac BJT Model Drawn in the Shape of a "T" Model. . 23 24 Fig. 1.9 Simplified Analog Circuit Analysis Fig. 1.9a Simplified BJT Amplifier Circuit Fig. l.9b Circuit with BJT Transistor Replaced by its T Model [The analysis in equations 1 and 1a finds the input impedance, Z IN VIN I IN , needed to find the voltage gain for the circuit Using this information, equations 2a and 2b can be written to find the voltage gain, Av.] 24 25 Fig.1.9c Sketch of the Output Waveform, or Signal, for an Input Signal with an amplitude of one millivolt. [Note that the output waveform is out of phase with the input waveform.] Fig. 1.10An Example of Analysis of the Analog Signal Gain for a BJT SingleStage Amplifier. Box around the + sing means that this is the polarity assumed. If the polarity result is opposite, the answer is given a minus sign to indicate the actual phase relation between the input and output. Fig. 1.10a Circuit Usually just the + signs are shown, without the boxes. Notice the + signs at the input. C Given: VCE 4 v ; IE 1 mA ; =99; re 25 mV 25 IE mV +1 re 2.5K 25 26 Fig. 1.1B Step by Step (a, b, and c) Analysis 26 27 Fig 1.11 In Class Exercise: Reflecting the Large Signal Input Voltage Off the Diode Characteristic and its Linear Approximation. Note that points (a) and (b) have been done for you. Repeat the exercise for the small signal, using a different color pencil, if possible. Use the characteristic curve, not the tangent. What would the shape of the output current be if the tangent was used instead of the curve? 27 28 Fig 1.12 Basic Model for an Amplifier and Analysis of Example Circuits. Fig 1.12a Basic Model with Example Values for Impedances and Gain. R I =Amplifier Input Impedance R S =Signal Source Impedance R o =Amplifier Output Impedance VS =Signal Source Voltage A V =Amplifier Gain R L =Load for Amplifier to Drive vo vS =Overall Voltage Gain Fig. 1.12b Analysis of Example Circuits 28 29 Check the Answers for the Examples! What Conclusion Do you Draw About the Desired Values for RI and Ro for an Amplifier? [Find the overall voltage gain, vo vs , of the amplifier circuit for the given Rs and Ro values.] 1 RS 103 RL 10 VI 106 Vs V 10 VS ; Vo 103VI 500Vs o 500 3 6 10 10 10 10 Vs 2 RS 106 RL 10 VI 106 Vs V V 10 s ; Vo 103VI 500VI 250Vs o 250 6 6 10 10 2 10 10 Vs 3 RS 106 RL 1 VI Vs V 1 V 10 ; Vo 103VI Vo 103 s 45.45VS o 45.45 2 10 1 2 11 Vs 4 RS 9*106 RL 1 VI 5 RS 108 RL 1 VI 6 V V 1 V 106 10 s ; Vo 103VI Vo 103 s o 9.09 6 6 10 9*10 10 10 1 2 11 Vs V 106 1 0.01VS ; Vo 103 0.1VS 0.909VS o 0.909! 6 8 10 10 11 Vs V 106 104 3 RS 10 RL 10 VI V VS ; Vo 10 VI 103VS o 103 6 s 4 10 10 10 10 Vs 4 Fig. 1.13 Characteristics and Equations for the JFET Device and Comparison with the MOSFET Device 29 30 VCD mV The threshold voltage and the pinch-off voltage are different names voltages on the transfer characteristic. Note that the transfer characteristics for Junction Field-effect Transistors are the same as for the transfer characteristics for depletion mode MOSFETs for gate to source voltage less than zero, even though the devices are physically very different 30