Download Lesson One

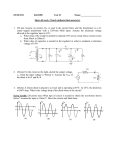
1
Key Lecture Concepts for EE 372 (Mostly Analog Electronics) by R.H.Cornely, Aug 24, 05
All Copyrights Reserved [Sentences in these notes that are enclosed in brackets contain information
that may be interesting and important but can be left unread until the entire lesson is learned.]
LESSON ONE: Introduction to Analog Electronics; Overall View of Electronics
OVERVIEW AND OBJECTIVES: Lesson one presents an overview of the subject of circuits
for analog signals and introduces most of the key concepts used in the course. It is expected that
it will take several weeks of study before these concepts are mastered. Thus the parts of lesson one
which are not understood should be read every three or four days until the lesson is mastered even
while studying lessons 2, 3, and 4. The assigned problems and the solved examples in this lesson,
and in all the lessons, should be practiced often and discussed in class to exercise the concepts.
An analog signal usually represents a physical or chemical variable such as temperature, sound,
electromagnetic waves (light), magnetism, and electrical current. The amplitudes of analog
signals can have any value; i.e. they vary continuously or smoothly with time, e.g. as a sine wave,
as opposed to the on/off, high/low values for digital signals. The variations can occur slowly as in
the case of mechanical vibrations of a building or the temperature variations within a classroom. On
the hand, analog circuits that can amplify very high frequency changes, in e.g. electromagnetic waves
received by an antenna, are also required. In this information age, “very high frequency” refers to
frequencies at gigahertz rates and higher. [Analog signals generally have time variations with
different frequency components, e.g. representing e.g. the various sounds of musical instruments. Thus
the frequency response of a hi-fidelity amplifier of analog signals is an important characteristic of
amplifier of audio signals received from a sensor of sound, i.e. a microphone.]
A sensor is a device that converts an input signal in the form of one type of energy (e.g. light)
to an output signal in the form of another type of energy, e.g. voltage. [If the emphasis is on
changing the energy form of the input (e.g. sound to current) the sensor is called a transducer.
Examples of sensors that convert energy to electricity are solar cells and photodiodes (light to
electricity), receiving antennas (e.g. radio waves to electrical signals), microphones (sound to
electricity), and digital cameras (arrays of light detectors that convert patterns of incident light to
patterns of charge that are moved on output lines to be digitized and stored in a memory chip).]
Very soft musical sounds can be converted to current by a microphone and then amplified by
electronic circuitry, i.e. an audio amplifier. To obtain loud sounds of the same music, the
amplifier output voltage could be connected to a speaker. To record the sounds, a magnetic
head device that converts the voltage to electromagnetic waves that magnetize a storage media,
i.e. magnetic tape, can be used. As another example, the electromagnetic radiation sent out from
the transmitters of astronauts needs to be selected from the radiation emitted by hot bodies as the sun
and stars. Since the unwanted background radiation, or noise, has many frequencies (broad
spectrum, the astronauts send their messages within a narrow frequency spectrum. The electronic
amplifier on earth is designed to selectively amplify just those frequencies and not amplify the most
of the frequencies of the background noise. An important focus of this course is how to design an
electronic amplifier to control the selected frequencies that will be amplified (its frequency
response) so the desired signals are amplified and unwanted signals (noise) attenuated.
1
2
The focus of this course is on small-signal analog circuits, i.e. sine wave signals whose
small amplitude and frequency vary with time. The objective of this lesson is to introduce
the key concepts for amplifying and shaping these signals. Small-signal analog circuits
process information in the form of voltages that are typically less than 100 mV. These
relatively tiny waveforms, or wiggles, are superimposed on top of DC voltages, of the
order of volts. The DC voltages bias the operating point (called the Q point) of the
transistors so that it is kept in a region of its I/V characteristic where the small signal
output current is a linear function of the small signal input voltage. Thus small signal
analog electronics is also called linear electronics. Recall that digital electronics is based on
exploiting nonlinear characteristics such as the output versus input transfer curves of devices.
Large-amplitude analog signals (e.g. signals with amplitudes greater than 100 mV) are discussed
in the last lesson of this course. Their analysis is based on the transfer curve concept in the
Electronics One course. An example of a large-amplitude analog signal is a ten volt sine wave
sent from the output of an audio amplifier to a speaker system.
This lesson introduces the bipolar junction transistor, BJT. The BJT consists basically of a
forward biased diode whose current is injected into a nearby reversed biased diode. The diodes
are both within the same piece of material that is the transistor structure. The BJT has some
advantages and some disadvantages versus its four-decade competitor, the MOST.
The output of both the MOST and BJT is in the form of small-signal current that is able to
“drive”, or control, either another transistor or an external “load”, e.g. a speaker. The input
to the transistor is a small-signal voltage. The load as a resistance converts the output
current to an output voltage. (The output voltage of course depends on the amount of output
current resulting from the input voltage. Thus the change in output current divided by its cause,
the change in input voltage, is an important property which is named the transconductance.
The transconductance is referred to as a figure of merit. Its value and dependence on DC
bias current and device size have entered every discussion, or argument, in which MOST and
BJT devices have been compared. To help remember this fundamental idea, note that
conductance means current divided by voltage. The syllable “trans” indicates that the
current and voltage are at two different locations or “on the other side of” as “transatlantic”
or “translation”.
An important objective of this course and lesson is to show how small signal transistor circuit
models for the BJT and MOST are used in the analysis and design of analog circuits. These linear
circuit models replace the transistors by resistors and dependent current sources, which
depend on the transconductance, so that linear circuit theory can be applied.
A final section of this long lesson focuses on the junction field effect transistor, JFET. This
knowledge is needed to prepare for experiments in the EE 392 Laboratory Course. The 392
course is often taken concurrently with EE 372.
2
3
A) Comparison of the Different Types of Electronic Circuits
There are four types of signals used in electronic circuits. They are Digital (DS), Small Signal
Analog (SSA), Large Signal Analog (LSA), and Mixed (MS). Pictorial representations of the
four types are shown in fig1. The amplitudes of the sketched waveforms have typical values.
Digital electronic circuits manipulate signals that have discrete amplitude levels, e.g. 0 and 3 volts.
Digital circuit design involves finding clever ways to use three terminal devices with nonlinear
characteristics, particularly the MOSFET, to perform digital logic and storage by quickly charging
and discharging capacitance. The capacitance is often parasitic (undesired); however, sometimes
capacitors are deliberately introduced, e.g. for charge storage elements for memory. This topic,
covered in Electronics One, will be studied again in the third electronics course with the active
MOSFET component replaced by other electronic systems composed of integrated circuits.
Analog electronic circuits have voltage and current waveforms that are not discrete but are
varying continuously (smoothly) with time. An input waveform, or signal, can have all
possible amplitudes. The amplitudes are proportional to the physical variables that they
represent. Examples of such variables are fluid flow rates, the sounds of an orchestra, light
intensity, magnetic forces, and temperature. An example of a large signal analog waveform is
shown in the upper right corner of fig1.1. The voltage waveform might represent the temperature
in a room that is varying between 70 and 62 degrees with the time scale in hours and the voltage
varying either about zero volts or about some DC value corresponding to an average temperature.
The amplitudes of the waveforms, as the variables they represent, can vary with time continuously
between positive and negative maximum values. Thus the analog signals can have any value
within a continuous range.
Usually the frequency of the total, or actual, signal is varying with time as in the case of the large
and small signal analog waveforms in fig1.1. The signal generally is made up of sine waves with
different frequencies and amplitudes that are summed together, or superimposed, to give the total
signal. Analog circuits often are required to amplify the total signal without changing its
frequency content, i.e. the relative amplitudes of the sine waves of different frequencies that
make up the actual signal. Thus all the signals with different frequencies have to be
amplified by the same amount. This is particularly challenging if the signal to be amplified has
significant frequency components in the gigahertz range required by broadband communications
systems. Therefore the designers of amplifiers of analog signals must be concerned with how the
amplification varies with frequency. This is called the frequency response of the amplifier.
In this course the analog circuits will be discussed and analyzed as if the input signal
representing a physical variable had a single frequency. The total response of an analog
amplifier to an actual input signal is obtained from the output responses to the different
frequency signals that make up the actual input signal. For analysis, the calculated responses to
input signals with different frequencies can be superimposed, or added together.
If the amplitudes of the signals are "small enough”, the transistors in the analog circuit
that amplify the total signal can be represented by linear circuit models. An example of a
small analog signal is the signal shown in the lower left corner of fig1.1. It looks as if it is a small
wiggle of the order of 1.0 [mV] riding on top of 1.0 volt DC.
3
4
For input signals with “small” amplitudes, a linear transistor model can approximate the
nonlinear three terminal device characteristics. The model consists of linear resistors and
dependent current sources. Examples of the small signal circuit models and symbols for the
two types of transistors used in analog circuits, MOST and BJT, are shown in fig1.2.
[Capacitors must be added to the model, as shown, if the signal frequencies are high enough to
cause time delays between the output and input. Note the capacitors dotted into the BJT and
MOST models.]
The analog circuits can be analyzed when the input signal is “small” by replacing each of the
actual transistors in the analog circuits by its small signal circuit model and performing circuit
analysis as done in the Circuits One course. [However, a more effective approach will be taught in this
course that will simplify analog circuit analysis and design particularly when the circuit has more than
two or three transistors.] The values for the resistors and other parameters for the components in
the small signal circuit will depend on the DC voltages and DC currents of the 3-terminal
transistors. Approximately one third of the analytical work in this course will be DC analysis of
MOST and BJT circuits. The purpose of the DC voltages, or currents, is to bias the transistors
so that they operate at a Q point on the device characteristic. The Q point should be located
where the transconductance has its highest value and required output current variations with
time are not distorted with respect to the shape of the input waveform. [Do you recall finding the
Q points for diodes and MOS transistors in Electronics One using DC linear models? A battery and
resistor to approximate the nonlinear diode curve were used.] To effectively amplify the ac input
current or voltage, a three-terminal device must be properly biased into a region that can
produce an output that is linearly proportional to the input signal.
Large signal circuit analysis is required when the amplitude of the input signals are large
enough that the small signal circuit models do not accurately predict the circuit behavior. In
Electronics One you learned how to use DC models for two terminal nonlinear diodes and to use
voltage transfer characteristics to relate output voltages to input voltages. The techniques for analysis
of circuits with large signals are similar to these and will be discussed in the last lesson of the course.
A fourth type of electronic circuit is one that converts analog signals to digital, or vice versa.
These circuits could be called mixed. An example of a possible waveform in such a circuit is
shown in the lower right of fig1.1. Note that discrete voltage levels are superimposed on top of an
analog signal. An example of a mixed circuit is the computer modems that convert analog telephone
signals to the digital signals used in the computer. These circuits, not covered in Electronics Two,
can be understood using the basic concepts for the other three types of circuits.
B) Small Signal Linear Models for Representing Nonlinear Devices
To introduce the concept of small signal circuit models, we will first study the diode and then
the closely related three-terminal device, the bipolar transistor. The graphs and equations in
fig1.3 summarize how the nonlinear diode can be treated as a linear resistor for analog signal
waveforms with small amplitude. The diode equation for the characteristic in fig1.3a is the
familiar equation 1 at the bottom of the figure.
4
5
The diode voltage will normally have two components: a DC voltage that has the symbol VD
(which biases the device, or puts the Q point at a desired location on the I/V characteristic) and a
small, time varying voltage, vd, the analog signal. This small signal input could be a voltage of
amplitude vd that varies sinusoidally with time. The "output", or the response to the input, is the
current which also has a DC component, ID, plus an ac component id, with the symbol for their sum
being iD. Please adopt the habit of writing upper case letters and subscripts if a symbol is for
DC currents or voltages and lower case letters and subscripts for ac currents or voltages. For
total voltage or current values (DC plus ac components) use a combination of lower and
upper case letters as shown under fig1.3a.
In fig1.3b the portion of the curve involving the input signal is magnified and the region around the
DC bias point, or Q point, corresponding to VD and ID, is enlarged. The total current at each
instant of time can be obtained graphically by reflecting each input value off the characteristic curve at
times t1, t2 , t3, etc. to obtain the current waveform, as shown in fig1.3c. Again, the value of current at
each moment of time (t1, t2, t3 etc.) can be found by extending a line from each value of input voltage
(for each moment) upwards and reflecting the line off either the actual diode curve, as in fig1.3c. This
method is also applied in fig1.3d but the linear approximation rather than the diode curve is used.
From the difference in the outputs, for the two different reflections, one can appreciate how the
distortion of the output current would become worse as the input voltage becomes larger. (Distortion
refers to the output current not having the same shape as the input voltage.) The graphical analysis is
more easily done with triangle versus sinusoidal inputs, as in fig1.3e and the exercise below.
Exercise 1.1 Refer to fig1.11. Complete the sketch of the output current for the two
triangular input voltages by reflecting the input voltage off the nonlinear diode curve, not
its tangent. Note that there is much more distortion for the large amplitude input because
the reflections are from the part of the diode curve that has more curvature.
Refer to fig1.3c. Note that if the ac voltage signal is zero, the output current is simply the DC
current ID. Note also that because the sine wave voltage input is "large", the current waveform is
not a sine wave because the diode characteristic is nonlinear. If the ac voltage, vd, is small
enough, the nonlinear curve can be taken to be a straight line tangent to the curve in the
neighborhood of the Q pt. as shown in fig1.3d. There will be no significant error, or difference
between the current waveform reflected from the actual curve versus the straight line, the
approximation of the curve, if the signal is "small". The sine wave component of the voltage
applied to the diode will cause a current id that will also be a sine wave, with the same frequency
as the ac component of the “input” voltage. The amplitude of the current will be proportional to
the small signal conductance, which is the slope of the diode curve. [If the curve is steep, the
resistance will be smaller and there will be more ac current.] Fig1.3e shows that the reflection
method can be applied to any arbitrarily shaped signal.
An important result is given in equation 3 at the bottom of fig1.3. It is derived by differentiation of
equation 1, as shown by equation 2. It follows as shown by equation 3 that the ac conductance of
the diode is proportional to the DC current divided by the thermal voltage times the ideality factor,
n. [This assumes the normal condition of ID being much greater than the reverse saturation current,
IS.]
5
6
The key result to memorize is that the diode resistance is inversely proportional to ID, as
shown in equation 1 below. Thus the DC Q pt. parameter, ID, controls the "voltage to current
conversion gain" of the device.
1) = 3a) r = vd / id = nVT / ID
r  25 mV / ID [mA]
(assuming nVT = 0.025 V = 25 mV)
For convenience in this course 25 mV always will be taken as the value of the thermal voltage
times the ideality factor, although actually it is a variable that depends on the ambient
temperature. Equation 1 is used often to connect the DC world to the ac world.
Figs1.3c, d, and e show that during the time when the total input voltage is greater than the DC
voltage the total output current is greater than the DC diode current. When the voltage is less than
VD, the output current will be less than the DC current. The small signal current adds to and
then subtracts from the DC bias current as time varies, i.e. the signal current flows into the
anode when the ac diode voltage is positive and away from the anode when the ac voltage is
negative. The ac voltage and current are said to be in phase since when one waveform is
positive the other is positive. If they were out of phase they would have opposite polarities at
the same time. The concept of phase is very important in analog electronics.
In small signal analysis and design, it is convenient to use superposition theory and work
either with the DC currents and voltages or with the ac voltages and currents, but never at the
same time. Thus for an analysis problem, we will put on our “DC hat” first and do a DC
analysis. Then we will put on our “ac hat” and do ac analysis to find the result we seek. [Have
you ever notice anyone wearing two hats at the same time? Do they appear to be able to able to
accomplish anything?] Thus there is a need to have an ac model for the diode as well as the DC
diode models that were used in digital electronics.
Based on the previous discussion, the ac model for a pn junction is simply a resistor, as shown
in fig1.4. Also shown is one familiar DC model. [In this course the value for the DC voltage for
the battery will be chosen to be either 0.6 or 0.7 [v], although any value between 0.3 and 1.4 [v]
could be a reasonable choice, depending on the diode, its material and structure, the biasing current
and the temperature. The resistance in series with the battery is often very small compared to the
external biasing resistors; thus it will be usually neglected in this course.] For the FET and BJT
three terminal devices, an input ac voltage will be applied across two “input” terminals and the
resultant small signal current from a third terminal is the “output”. The ratio of the output current
variation, or wiggle, to the input voltage wiggle is defined as the transconductance. This is
THE MOST IMPORTANT PROPERTY of any three terminal electronic device. As stated
earlier, the syllable "trans" is added to the word conductance because the voltage is applied to one
terminal and the output current is taken from a different location or terminal, unlike the diode.
C) The Bipolar Transistor (BJT), Two Closely Coupled Diodes
Fig1.5 introduces the BJT and its DC and ac circuit models. Observe carefully the symbol and
structure for the NPN and the PNP bipolar junction transistor shown in fig1.5a. The BJT consists
of 3 semiconductor regions: emitter (E), base (B), and collector (C); observe that there are two
PN junctions.
6
7
For an NPN BJT the emitter can be considered as a source of electrons that “throws” them
at the collector. The emitter region is much more heavily doped with impurities added to the
host silicon atoms than the collector region. This causes an electron enrichment of the E region
as indicated by the plus sign next to the N in the structure. The base terminal has the role of
enabling forward bias voltage to be applied between the base and emitter diode. This voltage
causes the injection of electrons from the emitter that flow towards the collector, passing
through the thin P-type base region. The base region is kept thin to enable the electrons to
pass quickly through the region before they have a chance to recombine with the holes of the
P region. [The oppositely charged carriers attract each other and recombine if they are given
enough time. This time to recombine is called the recombination time, or just lifetime. With the
mobility parameter, it is the most important property of semiconductor material. Thus the thickness
and doping level of the base region controls the electron current flow through the reversed biased
collector-base diode to the collector terminal.]
As described above, the base region unfortunately tends to capture a small percentage of the
electrons flowing from the emitter to the collector. Thus the collector current always will be
slightly less than the emitter current. The transistor is designed so that the base region is as thin
as possible to reduce hole flow from the metal contact into the base to make up for the holes that
are “grabbed” by the oppositely charged electrons. [Holes most flow into the base to maintain total
charge neutrality, summation of all charges equal to zero. In modern transistors the base region is
as thin as 0.1 microns or less, i.e. about 300 atomic layers. For PNP transistors, the function of the
emitter is to shoot positively charged, mobile holes towards the collector in response to forward
bias between the base and emitter diode.]
The BJT can be modeled for normal operation by a diode between the B and E terminals and
a dependent current source between the C and B terminals, as shown for the NPN and PNP
in fig1.5b. [Normal bias is when the EB junction is forward biased and the CB junction reversed
biased.] The value of the dependent current source is the DC Beta times the base current IB,
or equivalently DC Alpha times the emitter current IE. [Alpha, , and Beta, , are related by
equations shown at the right-hand margin in fig1.5b. They are usually given convenient
values in this course of 0.99 and 99.] The current directions when the emitter-base junction is
forward biased are shown in fig1.5b. The value of Beta can be more than 1000 or as small as
30. Thus the base current is normally very small and IC only a slightly smaller than IE.
Exercise 1.2 Derive the equations shown at the right-hand side of fig1.5b. They are useful to find
alpha when beta is given and vice versa. The base-emitter diode current is the emitter current,
IE. For both the PNP and NPN, IE = IB + IC. Hint: Use  ≡ IC /IE and  ≡ IC / IB
When both junctions are reversed biased, the transistor is biased in the cutoff region and all
currents are ideally zero, although actually small leakage currents related to the diodes reverse
saturation current and the transistor's Beta actually exist. Although there are four possible bias
regions, saturation and reverse active being the names for the other two, analog circuit
operation requires that the transistor be biased in the active only. [Four corresponds to the
four possible biasing combinations for the base-collector and base-emitter junctions. Each
quadrant of the BIAS SPACE plot, fig1.5d, is for different possible combinations of forward and
reverse bias for the BC and BE junctions.
7
8
In the cutoff region, the base-collector and base-emitter diode junctions are both reversed biased,
as indicated by the signs of the voltages applied to the junctions. In the saturation region, both
junctions are forward biased. When designing the bias circuit for non-distorted amplification of
small signals, these regions are to be avoided under all operating conditions.] Note the useful
equations in the table under fig1.5d with equations useful for relating the three BJT currents.
Exercise 1.3 (optional). Construct a Bias Space figure for a PNP transistor.
D) DC Analysis of BJT Circuits
The objective of DC analysis is to find the Q point values for the BJT: that is the values for
either IC or IE and for either VCE (if the transistor is a NPN) or VEC (if the transistor is a
PNP). [The Q point values are needed because the values of ac parameters in the transistor
models depend on the DC biasing of the transistors, i.e. the Q points.] The analysis can be done
in three steps as presented in the text at the left of the first example in fig1.6. As you read
each step, refer to the equations in example 1 (for a PNP) at the right of the steps. As previously
explained, for convenience the value for eta is taken to be 99, although modern BJT
transistors have values up to 10,000, or more. A reasonable value of 0.6 [v] for VBE (and for
VEB for a PNP) are assumed for the examples. [Actually the diode voltage depends on the
diode current, IE. However, in this course we will not take the time to find the exact value as was
done in Electronics One. The diode equation for the diode voltage as a function of current shows
that for various practical emitter current values the emitter-base voltage will usually between 0.5
and 0.8.] [Recall from figs1.5b and 1.5d that  = /(1+  )].
Step 3 is a necessary check to see if the voltage between the collector and the base is such
that the collector base junction is reversed-biased. If it is, then the Q point values are
correct. If it is forward biased by more than about 0.4 volts, current will be injected from
the base into the collector independent that is in the opposite direction of the normal
collector current. The collector current will not equal Beta times the base current but will
be less. The transistor is said to be in the saturation region and a saturation model for the
BJT would be used to find the Q point. However, further analysis is not necessary in this
analog electronics course since the transistors must be biased in the active region for normal
applications. [For future reference after this course, bias space sketches summarizing the four
possible regions of PNP and NPN transistors is given on the third page of figure 6. The use of the
equations relating beta and alpha assumed that the BJT was in the active region. If the method
given is used the voltage drops will always be positive values unless the transistor is incorrectly
biased into the saturation region. The homework drill exercises will have some transistors biased
into the cutoff and saturation regions to exercise your understanding.]
Three other examples of how to find the Q point values for a BJT circuits are given on page 2 of
fig1.6. The solutions for the examples should be studied and then practiced without referring to
the solutions. For example 2 note that the first equation can be immediately written in the form
of equation 1a, since the value of the emitter current is sought. [Note that if there are two or more
resistors in the base biasing circuit, the Thevinin equivalent theory can be used to reduce the circuit to
a single resistor and a modified base supply voltage. This will be done later in the course.]
8
9
Exercise 1.4 Study again the four examples of Q point analysis in the class handout and then
do the assigned drill problems for PNP and NPN transistors. These problems will be handed
out in class. If your analysis shows that the junctions are both reversed biased, it should be noted
that the BJT is incorrectly biased in the cutoff region and no further work needs to be done.
Similarly, if both junctions are forward biased, it should be noted that the transistor is incorrectly
biased in the saturation region and no further work done.
E) Introduction to Small Signal Analysis of BJT Circuits
Small-signal ac analysis is done without concern for DC voltages and currents by using
superposition, just as explained for the diode in section B. First the DC currents and voltages for
the BJT are found by DC analysis, to determine the parameters in the ac circuit model for the BJT.
Then the ac analysis is done using the circuit models in fig1.5c. Looking at the ac models in
fig1.5c, note that the models for the PNP and NPN transistors are the same. The direction of
the arrow of the dependent current source depends only on the polarity (phase) of the voltage
across the BE junction and not on whether the BJT is a PNP or NPN. This is because the B-E
junction is modeled as a resistor and the directional property of the diode is no longer a
factor. When the ac voltage at the base relative to the emitter is positive (as indicated by the + sign
on the base and the negative sign on the emitter), the current increases in the direction of base to
emitter. As a result the collector to base current increases as indicated by the arrow next to the
ac symbol for collector current. On the other hand, as the voltage at the base relative to the
emitter decreases, as indicated by the positive polarity of the voltage between the emitter and base,
the ac current flows from the base towards the collector. Understanding this phase relation is
very important.
Fig1.7 is designed to help you understand the concept of superposition of the DC and ac
analyses. Study this figure carefully. Also review fig1.8 which shows the ac model drawn in the
shape of the letter T. Note that this circuit model for the transistor is identical to the model in
fig1.5c; however, it is twisted into a letter T shape so that it is easier to see that the vbe voltage
is the input and the dependent current source is the resultant output. This output current
can be pushed through a load resistor to provide an output voltage that can be much larger
than the input voltage. Thus the transistor can provide a voltage gain; that is, the ac voltage
across the load resistor, the output signal, can be much greater than the voltage input signal
across the base emitter junction, re. [Please note again that capital letters for the current and
voltage symbols and subscripts are used for DC, while lower case letters are used for ac.]
F) Examples of Analog Circuit Analysis
The voltage gain and input impedance for a simplified BJT circuit will be found in the first
example. The BJT circuit, in fig1.9a, has only an ac input vIN. The DC bias circuitry is left out to
simplify the circuit. The first step in the analysis of this circuit is to redraw the circuit by replacing
the BJT component with its “T” circuit model as done in fig1.9b. The “T” circuit model is drawn
first and then the components attached to the e, b, and c terminals in fig1.9a are connected
between the corresponding terminals of the model in fig1.9b and the rest of the circuit. For
this simplified circuit example the only component to attach is the 10K resistor to VCC. Note
that in fig1.9b the resistor was placed between the collector terminal and ground and not a
DC voltage. VCC was replaced by ground, since DC voltages are shorts for ac signals.
9
10
If the voltage on one side of a battery, or power supply, is increased by some value, the voltage on
the other side is increased by the same amount, as shown in the insert at the right of circuit in
fig1.9b. [Please remember that DC voltages are shorts in the “ac world” and DC current
sources are open circuits.]
In the analysis under the circuit in fig1.9b the input impedance, Zin, which is defined as the
input voltage vin divided by input current, iin, is found by setting the input voltage equal to the
IR drop across the ac emitter junction resistance, re. Note that the current flowing through this
resistance is more than the input current! The result is that the resistance of the base emitter
diode, re, is effectively increased by ( + 1). [The changing of the apparent value of impedance
between two terminals by transistors is a key concept in analog electronics. Once the
application of this concept is mastered, the analysis and design of circuits with more than one
transistor can be easily done without redrawing the original circuit, as was done in fig1.9b.]
The voltage “gain”, v0/vin, is found by the analysis initiated by equations 2a and 2b. Please practice
finding the voltage gain (− 400) by copying the circuit in fig1.9a on a sheet of paper and repeating
the work done in fig1.9b. Also please study the time, or phase, relationship of the output and input
voltages in the Phase Analysis under the circuit and note the resulting out-of-phase relationship of
the waveforms in fig1.9c.
The example in fig1.10 presents an overview of the key concepts and techniques that are used to
analyze analog circuits. For simplification purposes it is assumed that DC analysis has been done
previously and that the DC emitter base diode current, IE, was found to be 1 mA. [The DC analysis
would be done as in the problems in exercise 1.4 by using the circuit with the DC biasing voltages
VBB and VCC and the 2.5 M base biasing resistor connected to the base-emitter diode.] The role
of the capacitor is to isolate, or protect, the ac input source from the DC voltage at the base.
Note again that since DC voltages are shorts for ac signals, the biasing voltages can be
replaced by ground for ac signals. As previously mentioned, the DC and ac Betas were given as
99, a convenient value to work with. [Normally ac and DC beta values for a BJT are e.g.10%
different when the device characteristics are measured; however, in many textbooks, such as
Jaeger and Blaylock, the DC and ac beta values are taken to be equal]
The emitter base diode resistance is calculated to be 25 ohms. Multiplying that value by  +1
(i.e. 100), the input impedance between the base and emitter junction is found to be 2.5 K.
That value is then put into a box on the circuit diagram, with an arrow pointing in the direction
of the base. The box is used to highlight this important and useful result. All the circuitry to the
right of that box can be treated as a resistor of 2.5Kattached from the base to ground.
Understanding and applying this concept is a crucial for analysis of more complicated
circuits. If there are any questions about the concept please bring them to the attention of the
instructor and exercise the ideas in discussions with classmates and instructor during the class.
The steps a, b, and c in fig10b are done after the input impedance is found and put in the box.
They are the critical first steps to find the voltage gain of the circuit. After they are done it is
straight-forward to write equations for the base and collector currents, ib and ic, as done in equations
1 and 2. The output voltage and input voltages can then both be written in terms of the base current,
as in equations 3 and 1a and the voltage gain, Av, found as shown in the lower left corner of the
figure.
10
11
To obtain a quick and reasonable result, the 2.5M resistance to ground was neglected compared
with the 25K input resistance. Thus two of the three parameters of interest for any small signal
amplifier (the input impedance, the voltage gain and the output impedance) have been found.
Note the 180 degree shift, phase relationship, in the plots of the input and output voltages. [The
analysis at the lower right side shows that neglecting the shunting of input current by the
2.5Mresistor has little effect on the voltage gain. However, the current division approach
accounting for this shunt to ground effect will be important in other problems.
The importance of input and output impedance in analog electronics cannot be overemphasized;
it will be taken up in more detail in lesson 2 and used in each of the remaining hours of the
course!
Exercise 1.5 Draw the circuit at the top of fig1.10 on a sheet of paper. Without looking at the
solution in the figure, find the voltage gain and compare your answer with the value of – 283.
Sketch the output waveform for a sinusoidal input of five microvolts.
Exercise 1.6 You speak into a microphone at a radio studio. Your friend tells you a week later
what he heard and you smile. What different forms of energy related to the voice signal
occurred during this week?
G) The Basic Model for an Amplifier and Examples of Limits on its Effectiveness
A small signal amplifier can be modeled in terms of its input and output impedance and its
voltage gain, as shown by the model circuit in the amplifier “box” in fig1.12a. Example
values for the input impedance, RI, and output impedance, R0, and the voltage gain, AV, are
given in parentheses. Note that the impedances of the amplifier are fixed, and modeled as
internal or “in the box”. This amplifier may not be necessarily effective for the loads it may
have to drive and for the signal sources driving it as shown by the examples. In the example
problems in fig1.12b the amplifier, with the given values, is driven by signal sources with
different values for the signal source impedance and with various loads attached to the output of
the amplifier. The examples are designed to show how the overall signal gain, v0/vS, depends on
not only the voltage gain of the amplifier, AV, but on the ratio of the amplifier input impedance
to the sum of the input impedance plus the signal source impedance. The gain also depends on
the ratio of the load resistance to the sum of the load resistance and amplifier output resistance.
Exercise 1.7 Practice the examples given in fig1.12b and do problems presented without
solutions in class. Can you answer the question in fig1.12b? Explain all the critical factors to
achieve large overall gain in an amplifier circuit.
H) The Junction Field Effect Transistor
Fig 1.13 summarizes the JFET device characteristics, as done for the four different MOS
transistors in the notes for Electronics One. The characteristics of the device are basically the
same as the depletion mode MOST (DMOS) except that the n-channel device can not be
operated with the gate to source voltage more than a small positive voltage or the gate draws
significant current.
11
12
[This results in the loss of the isolation between the gate and the source, critical for the field effect
device to function.] From the drain characteristic it is seen that as for the DMOST there is a
linear region where the device acts as a voltage controlled resistor, with VGS the voltage that
changes the resistance. There is also a saturation region, or constant current region. If the Q
point is in that region, the device acts as a “constant” current source with a current value
largely independent of the drain to source voltage.
The current in the saturation region can be changed by changing the gate to source voltage,
as shown by the transfer characteristic. [The physical operation of the device is based on the
widening of the depletion region of a reversed biased diode which effectively changes the
resistance between the drain and the source, and thus the current for a fixed drain to source
voltage. The physical operation is entirely different than that for the MOST, which is based on
changing the carrier concentration, thus the conductivity and source to drain resistance, of the
electrons which carry the current between the source and the drain.] The equation for the JFET
saturation region, equation 1, has the same form as the equation for the MOST. Thus if K for
the DMOS equations is replaced by (2IDSS)/(VP)2, where IDSS is two times the saturation
current for VGS = 0, equation 1 is obtained.
The threshold voltage for a DMOS corresponds to the pinchoff voltage, VP, for a JFET. Thus
the values for RON and gm can be found from values for the pinchoff voltage and IDSS from
measured characteristics on a curve tracer similar to the curves in the upper right of the
figure. The equations for the JFET and MOST in the saturation and linear regions are given
and compared in the figure for your convenience. For small signal inputs the JFET if biased
in its linear region can be replaced by RON = r. If it is the saturation region, the device can be
represented by the model for the MOST shown in fig1.2, with the capacitors replaced by
open circuits if the signal frequency is relatively small.
I) Summary You have achieved a reasonable mastery of this lesson when you can understand
and solve on your own the examples in figs1.10, 1.11 and 1.12 and can do the BJT DC analysis
exercises, similar to the examples in fig1.6. DC analysis of MOST circuits was studied in the
Electronics One course and will be reviewed and used in later lessons.
12
13
Fig. 1.1 Examples of the Four Types of Electronic Signals
Fig.l.2 Examples of Small Signal Models
13
14
Fig. 1.3 Small Signal Modeling of the Diode
Distorted a
output iD
sine wave
input, v D
1 iD  ISe VD
nVT
-IS
2  δi D δv D  I S e vD nVT  nVT   I D +IS  nVT =g d
Ideality factor, n: 1<n<2;
Thermanl voltage, VT : VT  k T q ; nVT  25mV
Therefore,
3 g d  I D nVT  I D  mA  25  mV  or 3a  rd  25  mV  I D  mA 
14
15
Fig. 1.4 DC and ac Circuit Models for the Diode
Input: vd  VD  vd
Output: i D  I D  id
Input: vD  VD  vd
Output: i D  I D  id
15
16
Fig. 1.5 Symbols and a.c. Models for NPN and PNP Bipolar Transistors
a) Structures and Symbols for NPN and PNP Transistors
α
IC
IE
β  ICB
I
Transistor circuits are analyzed at one instant of
time and usually the "arrow down" model is used
unless the circuit has more than one transistor.
16
17
Fig. 1.5d Bias Space for an NPN BJT Transistor
Exercise 1.3 Complete the construction of a bias space figure for a PNP Bipolar
Transistor. Label the axes as shown.
Hint: when VEB and VCB are both positive, both junctions are forward biased and, the
BJT would be in its saturation mode.
Table 1.5 Useful Equations for Relating I B , IC , and I E .
17
18
Figl.6 Finding the Q Point of BJT Circuits; General Procedure and Three
Examples
Procedure: The Q Point is determined by finding either I C or I E along with
VCE (for an NPN transistor) or VEC (for a PNP transistor). The following steps
should, be taken to find the Q point: 1) Write a loop equation for the base
emitter loop by assuming a reasonable value for base emitter diode voltage
drop. (A reasonable value would be 0.4 to 0.75 [v].) For this course 0.6 [v]will
normally be assumed. Set the total voltage applied to the base emitter loop
equal to VBE (or VEB for a PNP) plus the sum of the IR drops across the resistors in
the base and emitter circuits. (Assume the convenient value for  of 99.) Write
the base current as the emitter current divided by  plus 1 when you first write
the equation to save time. Solve for the emitter current, I E (The collector
current can be found if needed by multiplying I E by a, i.e. 0.99 for   99 .
The base current can be found if needed by dividing the emitter current
by   1 .)
~
2) Find VCE ,or VEC ,by writing a loop equation for the loop from the collector
supply voltage to the emitter supply voltage. Set the total voltage applied to this
loop equal to the IR drops plus VCE ,or VEC ,and solve for VCE ,or VEC . (To save time
express the IR drop for the collector resistor in terms of the known value of I E by
using IC  0.99I E ).
3) Steps 1 and 2 were done by assuming that the BJT was in the active mode
and therefore that I c   I B . This assumption has to be checked, after the value for
the collector to emitter voltage is found, by seeing if the collector to base
junction is reversed biased or if forward biased has less than 0.3 volts so that
the diode current of the junction is negligible. An easy way to do this is to make
sure that VCE is positive for an NPN and greater than about 0.3 [v] and that VEC is
positive for a PNP and also greater than about 0.3 volts. If the voltage from the
C to E is 0.3[v] for and NPN, the voltage from B to C would be 0.3 [v], since the
voltage from B to E was taken to be 0.6[v]. (Check this statement by making
certain that the summation of voltages around the transistor loop is the equal to
zero.)
18
19
Example One
1 30.6  0.6  I E 1K 
IE
50 K
100
30
 20 mA
1K  0.5 K
2  50  I E 1K  VEC  0.99 I E
1a  I E 
2a  VCE  50  I E 1K  0.99 
= 50  20  19.8  10.2 V 
VE  10  I E 1K  10 V 
VB  10  VEB  10.6 V 
VC  40  0.99 I E 1K  20.2 V 
19.8
VCB  20.2   10.6   9.6 V 
VCB  9.6  R  biased
19
20
Fig 1.6 Continued THREE EXAMPLES
Example Two
BE loop:1 30.6  0.6 
IE
50 K  I E 1K
  1  100
30
 20  mA 
1.5 K
CE loop:2  40  0.99 I E 1K  VCE  I E 1k
1a  I E 
2a  VCE  40  19.8  20  0.2 V 
VE  0  20  mA 1K  20 V 
VB  VE  0.6
VC  VE  0.2  20.2 V 
VBC  20.6  20.2  0.4 V 
VBC  0.4 V  indicates BC junction is F-biased by 0.4 V  and the junction is
"almost" conducting BJT is at the edge of saturation. Assumption of BJT being
active is "just" OK.
0.2
20
21
Example Three
IE
30
50 K  I E 1K  I E
 20  mA 
100
1.5K
2  35  0.99 I E 1K  VEC  I E 1K  VCE  4.98 V 
1 30.6  0.6 
VC  35  19.8  15.7
VB  20  0.6  20.6
VBC  4.9
VBC  4.9 indicates both BE and BC junctions are F-biased and
 BJT is saturated and   99 VBE  0.75, VCE  0.2
Example Four
300 K 

BE loop: 4.1  0.6  I E 0.5 K 
 I E  1 mA
100 

EC loop: 15.4  1 mA  VEC  0.99*1 mA *10 K
VEC  15.4  0.5  9.9  5 V 
VC  13.4  9.9  3.5
VE  2  0.5  1.5 V 
VB  1.5  0.6  0.9 V 
VBC  0.9   3.5   4.4 and jct. R-biased. OK
BC junction R-biased means BJT is in active region
21
22
Fig 1.6c Bias Space for a PNP and an NPN Transistor
22
23
Fig. 1.7 Total Base-Emitter Voltage Waveform Decomposed Into Its DC and ac
Components.
Fig. 1.8 The ac BJT Model Drawn in the Shape of a "T" Model. .
23
24
Fig. 1.9 Simplified Analog Circuit Analysis
Fig. 1.9a Simplified BJT Amplifier Circuit
Fig. l.9b Circuit with BJT Transistor Replaced by its T Model
[The analysis in equations 1 and 1a finds the input impedance, Z IN  VIN I IN ,
needed to find the voltage gain for the circuit Using this information, equations
2a and 2b can be written to find the voltage gain, Av.]
24
25
Fig.1.9c Sketch of the Output Waveform, or Signal, for an Input Signal with an
amplitude of one millivolt. [Note that the output waveform is out of phase with
the input waveform.]
Fig. 1.10An Example of Analysis of the Analog Signal Gain for a BJT SingleStage Amplifier.
Box around the +  sing means that this is the polarity assumed.
If the polarity result is opposite, the answer is given a minus sign to
indicate the actual phase relation between the input and output.
Fig. 1.10a Circuit
 Usually just the
+  signs are shown, without the boxes. Notice
the +  signs at the input.
C
Given: VCE  4 v ; IE  1 mA ;  =99; re 
25 mV
 25
IE  mV
  +1 re  2.5K
25
26
Fig. 1.1B Step by Step (a, b, and c) Analysis
26
27
Fig 1.11 In Class Exercise: Reflecting the Large Signal Input Voltage
Off the Diode Characteristic and its Linear Approximation.
Note that points (a) and (b) have been done for you. Repeat the exercise for the small signal,
using a different color pencil, if possible. Use the characteristic curve, not the tangent. What
would the shape of the output current be if the tangent was used instead of the curve?
27
28
Fig 1.12 Basic Model for an Amplifier and Analysis of Example Circuits.
Fig 1.12a Basic Model with Example Values for Impedances and Gain.
R I =Amplifier Input Impedance
R S =Signal Source Impedance
R o =Amplifier Output Impedance
VS =Signal Source Voltage
A V =Amplifier Gain
R L =Load for Amplifier to Drive
vo vS =Overall Voltage Gain
Fig. 1.12b Analysis of Example Circuits
28
29
Check the Answers for the Examples! What Conclusion Do you Draw
About the Desired Values for RI and Ro for an Amplifier?
[Find the overall voltage gain, vo vs , of the amplifier circuit for the given
Rs and Ro values.]
1 RS  103  RL  10  VI 
106 Vs
V
10
 VS ; Vo  103VI
 500Vs o  500
3
6
10  10
10  10
Vs
2  RS  106  RL  10  VI 
106 Vs
V
V
10
 s ; Vo  103VI
 500VI  250Vs o  250
6
6
10  10
2
10  10
Vs
3 RS  106  RL  1  VI 
Vs
V 1
V
10
; Vo  103VI
 Vo  103 s
 45.45VS  o  45.45
2
10  1
2 11
Vs
4  RS  9*106  RL  1  VI 
5  RS  108  RL  1  VI 
6
V
V 1
V
106
10
 s ; Vo  103VI
 Vo  103 s  o  9.09
6
6
10  9*10 10
10  1
2 11 Vs
V
106
1
 0.01VS ; Vo  103  0.1VS   0.909VS  o  0.909!
6
8
10  10
11
Vs
V
106
104
3
RS  10 RL  10   VI 
V  VS ; Vo  10 VI
 103VS  o  103
6 s
4
10  10
10  10
Vs
4
Fig. 1.13 Characteristics and Equations for the JFET Device and Comparison
with the MOSFET Device
29
30
VCD  mV 
The threshold voltage and the pinch-off voltage are different names voltages on the
transfer characteristic. Note that the transfer characteristics for Junction Field-effect
Transistors are the same as for the transfer characteristics for depletion mode MOSFETs
for gate to source voltage less than zero, even though the devices are physically very
different
30