Download B - Instituto de Física / UFRJ

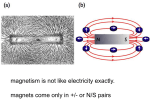
Física 3 - 2013/1
Instituto de Física - UFRJ
Campo magnético e
força magnética
Prof. João T. de Mello Neto
Referências
•
•
1.
2.
3.
4.
5.
Atenção: esta apresentação é apenas para uso interno
do curso de Física 3 - UFRJ 2013/1.
Referências:
Física 3, 12a. edição, Young e Freedman, Pearson Education do Brasil.
(Quase todas as figuras foram retiradas desta referência)
H. M. Nussenzveig, "Curso de Física Básica 3: Eletromagnetismo." Edgard Blücher, São
Paulo, Brasil, 1997.
P. A. Tipler & G. A. Mosca, "Física para Cientistas e Engenheiros 2: Electricidade,
Magnetismo e Óptica, 6a. ed." LTC, Rio de Janeiro, 2009.
Fundamentos da Física, vol. 3 (Eletromagnetismo), Quarta Edição, Halliday, Resnick,
Walker, Livros Técnicos e Científicos Editora S.A.
Outras citadas na apresentação.
MAGNETIC FORCES
Introdução
Imageamento por ressonância nuclear
permite o exame dos tecidos moles do
pé que não são visíveis por raios X. No
entanto os tecidos moles não são
magnéticos. Como a técnica de RMN
funciona?
Força magnética:
motores elétricos, circuitos de TV, fornos de microondas, alto-falantes...
Mais familiares: mã permanente, agulha de uma bússola.
Natureza fundamental do magnetismo: interação produzida por cargas
elétricas que se movem. As forças magnéticas só agem em cargas em
movimento.
Um conjunto de cargas em movimento PRODUZ um campo magnético. A seguir, uma
segunda corrente ou cargas em movimento reage a esse campo magnético e sofre a ação
de uma força magnética.
Neste capítulo: campo magnético DADO, como ele age em cargas e correntes??
next to each other. (b) The bar magnets
repel when
like
poles
(N
and
N,
or
S
and
S)
Interação entre magnetos
are next to each other.
(a)
Opposite
polesseattract.
Polos
opostos
atraem
S
N
N
S
F F
F F
S
N
N
S
(b)
Likeiguais
poles repel.
Polos
se repelem
F
F
S
N
N
S
N
S
S
N
F
F
an iron rod
magnetized.
its center, it
ordinary com
Before th
stood, the in
in terms of m
free to rotate
other end is
poles repel
magnetized
either pole
between a m
to electric in
ing that a ba
body respon
which varies with locatio
ins iron, such as a nail. (b) A real-life
Materiais não magnetizados
xample of this effect.
(b) Also, the magnetic field
t
d
)
b)
S
N
N
S
F
F
F
F
angle up or down is call
netic field is vertical.
Figure 27.3 is a sketc
field lines, show the dire
are discussed in detail in
be defined as the directi
27.3 A sketch of the eart
the earth’s molten core, cha
direction entirely at irregul
North geographic pole
(earth’s rotation axis)
O campo magnético da Terra
27.3 A sketch of the earth’s magnetic field. The field, which is caused by currents in
the earth’s molten core, changes with time; geologic evidence shows that it reverses
direction entirely at irregular intervals of 10 4 to 10 6 years.
Polo
norte
North geographic pole
geográfico
(earth’s
rotation axis)
The geomagnetic north pole is actually
Polo
norte geomagnético é
a magnetic south (S) pole—it attracts
um
sul magnético
the Npolo
pole of(S)
a compass.
Compass
bússola
Magnetic field lines show
the direction a compass
would point at a given
location.
S
The earth’s magnetic
field has a shape
similar to that produced by a simple
bar magnet (although
actually it is caused by
electric currents in the
core).
N
The earth’s magnetic axis is
offset from its geographic axis.
Polo
polo
The geomagnetic
sul geomagnético
é um
south pole is actually
a
north (N) pole.
magnetic
(N) norte
magnético
South
geographic
Polo
sul pole
geográfico
magnéticos
X cargas
elétricas
ieces arePólos
different
sizes. (The
smaller
the
iece,
the
weaker
its
magnetism.)
• Não existe nenhuma evidência experimental de pólos magnéticos
isolados (monopolos).
partida ao meio:
dois outros
imãs completos!
• Barra imantada
In contrast
to
electric
charges,
magnetic
poles
• Existência de monopolos magnéticos é um tema quente na física:
importantes
para acan't
cosmologia,
física de partículas,
always
comeconsequências
in pairs and
be isolated.
etc.
Breaking a magnet in two ...
N
N
S
S
N
S
(here viewed from above). When the comExperimento
de
Oersted
is placedconnected.
directly under
opass
be intimately
Overthe
thewire, the
compass
deflection
is reversed.
nifying
principles
of electromagnet-
S
(1819)
points north.
I50
(b)
principles
in
Maxwell’s
equations.
(a)
When the wire carries a current, the compass
electromagnetism, just as Newton’s
needle deflects. The direction of deflection
cs, and like Newton’s laws they repdepends on the direction of the current.
N
When the wire
intellect.
I
carries no
W
E current, the
.1 Suppose you cut off the part of the
N
compass needle
d gray. You discard this part, drill a hole
points north.
S
n the pivot at the center of the compass.
current is applied as in Fig. 27.5b?
❙
W
I50
I
N
E
W
S
I
I
(b)
When the wire carries a current, the compass
needlelet’s
deflects.
Theour
direction
of deflection
roperly,
review
formulation
Forças
magnéticas
:
produzidas
fundamentalmente
pelo
efeito
magnético
depends
on
the
direction
of
the
current.
we introduced the concept of electric
dos elétrons dos átomos no interior dos corpos.
two steps:
E
S
where
q ƒ is theismagnitude
of
the
charge
andBfare
is
ƒ
that
component
zero
(that
is,
when
and
v
S
agnetic
S
v
F
=
q
vB
!Bq, vas B
direction
of
v
to
the
direction
of
shown
in
the
force
is
zero.
rce.
F
=
=
q
vB
si
ƒ
ƒ
ƒ
ƒ
!
S
This
formB is sometimes
more
convenient,
This description
does
not
specify theThe
directio
Figure
27.6
shows
these
relationships.
direc
q
S
S
arge moving parallel tov a magnetic field
S
This
form
is
sometimes
more
convenient,
especially
+
always
two
opposite
toBcharge
each
other,
that
cular
to the
plane
vofand
. Its magnitude
where
isdirections,
theScontaining
magnitude
the
and
fw
i
harge moving
f to a magnetic
ƒ qSƒ individual
riences
zero at an angle
currents
rather
than
particles.
We
S
S
q
S
plane
of
v
and
Todirection
complete
d
experiences
a
magnetic
force
with
netic currents rather
direction ofparticles.
v toB.the
ofthe
B, description,
as discuss
shown in we
th
v
than
individual
We
will
0 vB sin f.
5 0 q this
e.
Fnot= specify
chapter.
thatThis
we used
to definedoes
the vector
inƒ qSection
ƒ qproduct
ƒ v! B =the
ƒ vB sin
)gnitude F 5 0 q 0 v!B in
S
description
directio
B
in this chapter.
SS q
to
reviewtwo
thatdirections,
section before
you go
on.) Draw
the
always
opposite
to
each
other,
tha
v
charge moving at an angle
f to a magnetic
F +
From
Eq.
(27.1)
the
units
of
B
must
be
the
S
S
S the
where
q
is
magnitude
of
the
charge
and
f
is
s perpendicƒ
ƒ
together,
as
in
Fig.
27.7a.
Imagine
turning
v
until
plane
of of
v Sand
B
. To complete
description,
w
Sthe
From
Eq.
(27.1)
the
units
B
must
be
the
same
as
th
ld experiences
a magnetic
force
Swith
r to the plane
direction
of
vis
to
the
of the
Bproduct
,to
as
shown
in s>C
the
(turning
through
thedirection
smaller
of
two
possible
an
B f. SI unit
5 0 q 0 vB the
sin
gnitude F 5 0 q 0 vq!Bfore
of
B
equivalent
1
N
that
we
used
to
define
the
vector
in
Section
S
taining
equivalent
to
1
N
s>C
m,
or,
si
S fore the SI unit of B is This
description
does
not
specify
the
direction
right
hand
around
the
line
perpendicular
to
the
pla
B
S f
to review that section before you go on.)
Draw
the
nd B.
S
S
S
v! coulomb
per
second
11
A
=
1
C>s2,
1
N>A
F
S
v
always
two
directions,
opposite
to
each
other,
that
v
B
.
around
with
the
sense
of
rotation
from
to
Your
arge
moving
at an angleper
f to a magnetic
s perpendiccoulomb
second
11
A
=
1
C>s2,
1
N>A
m.
This
u
together,
as
in
Fig.
27.7a.
Imagine
turning
v
unti
S
S
S
S
plane
of
v
and
B
.
To
complete
the
description,
we
rexperiences
to the planea magnetic force with
F
tion
of
the
force
on
a
positive
charge.
(Alternati
(turning
through
theof
smaller
of
the two
possible
ant
B
(abbreviated
T),
in
honor
Nikola
Tesla
(18
S
q
(abbreviated
T),
in
honor
of
Nikola
Tesla
(1856–1943),
0
0
0
0
nitude
F 5 q v!B 5 q vB sin f.
S
ntaining
that
we
used
to
define
the
vector
product
in
Section
1
F
on
a
positive
charge
is
the
direction
in
which
a
r
S
right
hand
around
the
line
perpendicular
to
the
pla
B
fS
nd B.
S the v
SDraw
v
American
scientist
and
inventor:
S
to
review
that
section
before
you
go
on.)
!
advance
if
turned
the
same
way.)
v
American
scientist
and around
inventor:
with the sense
of rotation from v toSB. Your
F
S
harge moving perpendicular to a magnetic together,
perpendicas in
Fig.F27.7a.
Imagine
turning
v
until i
This
discussion
shows
that
the
force
on
a
charge
tion
of
the
force
on
a
positive
charge.
(Alternat
S
S
d experiences
force
to
the plane a maximal magnetic
S
(turning
through
the
smaller
of direction
the
two
possible
ang
B
B
magnetic
field
is
given,
both
in
magnitude
and
q
1
tesla
=
1
T
=
1
F
on
a
positive
charge
is
the
in
which
ain
1
tesla
=
T
=
1
N>A
m
h magnitude
S
aining
S
right
hand ifaround
the
line
perpendicular
toSthe plan
B
fS
5 qvB. v S
dax B.
advance
turned
the
same
way.)
S
Fmax
!
v
S
S
v toon
Ba. Your
with
the S
sense
of rotation
from
t
charge moving perpendicular to a magnetic around
-4
-4
This
discussion
shows
that
the
force
charg
S
F
!
qv
:
B
(magnetic
force
on
a
mo
11
G
=
10
Another
unit
of
B,
the
gauss
T2,
is
also
in
co
S
11
G
=
10
Another
unit
of
B,
the
gauss
T2,
ld experiences a maximal magnetic
force
F
tion
of
the
force
on
a
positive
charge.
(Alternativ
S
S magnetic field B is given, both in magnitude and i
B
q +
th magnitude
Fof
on athe
positive
charge
isof
thethe
direction
in which
a ri
10
The
magnetic
field
earth
is
order
of
S
The
magnetic
field
of
the
earth
is
of
the
o
ax 5 qvB.
This
is
the
first
of
several
vector
products
we
w
S
advance ifSturnedS the same
way.)
S
vFmax
fields
offields
the order
of
10
T
occur
in
the
of
atoms
arge moving
perpendicular
to aof
magnetic
magnetic-field
relationships.
It’sforce
important
n
F!
qv
:
B interior
(magnetic
force
on to
a ma
This
discussion
shows
that
the
on
a
charge
the
order
of
10
T
occur
in
the
interior
S
S
experiences a maximal magnetic
force
deduced
theoretically;
it is
an observation
on
B
magnetic field B is given,
both
in magnitudebased
and in
q
q
S
Campo magnético
ƒ ƒ
#
#
#
#
#
Produto vetorial
n of the magnetic force on a moving charged particle.
(b)
ction of magnetic force on a positive charge moving in a magnetic field:
S
S
1
S S
d B in the v-B
r angle).
e perpenCurl the
around
tion you
w points
acts.
S
S
F 5 qv 3 B
tail to tail.
S
If the charge is n
of the force is op
the right-hand ru
B
q
S
v
plano
3
q
2
S
v
Force acts along this line.
S S
v-B plane
S
v
1
F5
2
1
S
q
3
S
B
S
S
Right
Mão
hand!
direita
S
v
q
S
F 5 qv 3 B
d for both positive and negative charges. When q is neg-
27.8 Two charges of
S
velocity
in
the
same
magnetic
field.
The
If
the
charge
is
negative,
the
direction
in the same B field with
Produto
vetorial
magnetic
forces on the charges are equal in
of
the
force
is
opposite
to
that
given
by
magnitude and opposite magnitude but opposite in direction.
the right-hand rule.
mples of the relationships
negative charges. Be sure
S
1
B
.
S
q Eq. (27.2). We
force F in
S
2
way. Since fvis the angle
S
S
S
erpret B sin fF as
the3com5 qv
B
S magniS
S
notation the force
F 5 qv 3 B
Positive and negative charges
moving in the same direction
through a magnetic field
experience magnetic
forces in opposite
S
S
S
directions.
F 5 qv 3 B
S
S
v
q
B
y in problems involving
ss forces on currents later
the units of F>qv. There-
f
S
(27.3)
S
B
q1 5 q . 0
q2 5 2q , 0
S
v
S
S
v
B
f
S
S
F 5 (2q)v 3 B
rce F is the vector sum of the electric and magnetic forces:
S
S
S
S
Medida do campo
magnético
F ! q1E " v : B2com cargas teste(27.4
y
) If the tube axis
parallel to the
xis, the beamSis
deflected, so B is
either the 1y- or
2y-direction.
(b) If the tube axis is parallel to the x-axis,Sthe
beam is deflected in the 2z-direction, so B is
the 1y-direction.
y
S
B
S
v
S
S
F
B
x
S
v
z
feixe
de elétrons
Electron
beam
z
x
field line is tangent
the field lines are
Linhas
de
campo
magético
e
fluxo
to the magnetic
packed,
the
stronger
S
field vector B.
the field is at that point.
S
B
Linhas do campo
magnético não são
linhas de força
S
B
S
At each point, the
N
. . . therefore, magnetic
gnetic field lines produced by some common sources of magnetic field.
Linhas de campo(b)magnético
Magnetic field of a straight current-carrying wire
(a) Magnetic field of a C-shaped magnet
Between flat, parallel magnetic poles,
the magnetic field is nearly uniform.
S
To represent a field coming out of or
going into the plane of the paper, we
use dots and crosses, respectively.
B
S
B directed out of plane
I
S
B
I
I
I
S
B directed into plane
S
B
Perspective view
Wire in plane of paper
(c) Magnetic fields of a current-carrying loop and a current-carrying coil (solenoid)
I
I
S
B
I
I
Notice that the field of the
loop and, especially, that of
the coil look like the field
of a bar magnet (see Fig. 27.11).
S
B
S
Linhas de campo magnético
B
(b)
(a)
S
B
limalha de ferro
Linhas de campos magnéticos não tem um "fim"
ences to help it navigate.
Física e vida: lagosta do caribe
ences to help it navigate.
Física e vida: lagosta do caribe
Embora tenha um sistema nervoso relativamente simples, ela é
incrivelmente sensível a campos magnéticos. Ela tem uma bússola
magnética interna que a permite distinguir sul, norte, leste e oeste.
Ela também sente pequenas diferenças no campo magnético da
Terra que podem ajudá-la a se orientar.
The total
magnetic
flux through
the
surface
isFor
the
sum
of
theoncontribu
this
component
varies
from
point
to
point
surf
total electric
charge
enclosed
by
the
surface.
example,
ifthethe
£ B = B! A = BA cos f
Fluxo
magnético
individual
area
elements:
27.15 Thethe
magnetic
through
anflux
area
this flux
component
varies
from
to this
point
onasthe surface. We define
d£ B point
through
area
Selectric dipole, the total electric flux is zero becaus
ncloses
an
lement dA is
to d£
be Bto
d£
Bthis
flux
through
area as to the surface, then cos f =
B =perpendicular
! dA.
B happens
If defined
be
d£ B = B! dA = B cos f dA =
e is zero.reduces
(You may
want
to
review
Section
Gauss’s
law
flux
S22.3
S on(magnetic
S
S
=
BA.
We
will
use
the
concept
of
magnetic
flux
#
#
ic Field and Magnetic
d£
=
B
dA
=
B
cos
f
dA
=
B
dA
£ B =to £BBForces
dA
=
B
cos
f
dA
=
B
dA
B
!
!
The
total
magnetic
flux through
the
surfaceaissurfac
the sum
through
f there were
such
a
thing
as
a
single
magnetic
charge
(magnetic
L of electromagnetic
L
L
S
ing our study
induction
in Chapter 29.
the
individual
area
elements:
B
The
total
magnetic
flux through the surface is the sum of the contri
f
B
tal magneticThe
flux
a
closed
surface
would
be
proportional
'through
SI
unit
of
magnetic
flux
is
equal
to
the
unit
of
magnetic
fie
theFor
individual
areaconcepts
elements:
(This equation
uses
of vector
area and
surface
integral
th
2 the
Gauss’s
law,
which
always
deals
with
closed
11Sm
). This
unit
of in
area
unit
called
the
(1
hon
#
etic charge
enclosed.
But
we
mentioned
that
noWb),
£ B is
=want
B!todAreview
= weber
Bthat
cos fdiscussion.)
dA
= magnetic
Bin
dA
SSection
duced
22.2;
youhave
may
S points
L
L S Sout (magnetic
L
dA Wilhelm
ment
dA
in
Eq.
(27.6)
always
of
the
surfa
fluxs
physicist
Weber
(1804–1891):
ver been observed,
despite
intensive
searches.
We
conclude:
Magnetic
flux
is
a
scalar
quantity.
If
B
is
uniform
over
a
plane
£B =
B! dA =
B cos f dA =
B # dA
through
a
surfa
tions
of
magnetic
flux
involve
an
open
surface
with
(This
equation
uses
the
concepts
of
vector
area
and
su
L the same at all
Lpoints on
total area A, BthenL
B! and f are
the
surface,
a
2
#
1
Wb
=
1
T
m
duced
in
Section
22.2;
you
may
want
to review
thattw
d
campo
an ambiguity
of
sign
in
Eq.
(27.6)
because
of
the
dA
S uses
(Thisthrough
equation
theMagnetic
concepts
area
and
surface
t
is=is
a BA
scalar
If B integral
is uniform
total magnetic flux
a closed
always
£
= Bflux
cosquantity.
f zero.
uniforme
B surface
!ofAvector
#
tion
for
dA
.
In
these
cases
we
choose
one
of
the
two
1
T
=
1
N>A
m,
Also,
so
total
area
A,
then
B
and
f
are
the
same
at
all
points
duced
in
Section
22.2;
you
may
want
to
review
that
discussion.)
na
superfície
!
S
S
f =a 1plane
If B happens
to beside
perpendicular
to
thechoice
surface,
then cosover
and
Magnetic
flux
isand
a scalar
If B isconsistently.
uniform
“positive”
use quantity.
that
A = BA cos f
2 £ B = B!
#
#
1
Wb
=
T
m
1
N
=A,BA.
reducestotal
to £area
of=points
magnetic
flux
exten
mbolically,
thenWe
B! will
and
fuse
arethe
the1concept
same
at all
onm>A
the
surface,
B
If the elementIf Bofhappens
area dA
in
Eq.
(27.5)
is
at
right
to be perpendicular
ing our study of electromagnetic induction
in Chapter to
29.the surface, the
££BBdA
==flux
BBA.
= will
BA cos
B!
= B;
calling
the
area
,Awe
!the
reduces
toequal
We
concept
of(1
maT
In
Gauss’s
law
the total
through
afthe
closed
surfac
The
SI unit
of
magnetic
fluxelectric
is
to!
unithave
ofuse
magnetic
field
S
S
i
S
S
#
ing enclosed
our study ofby
electromagnetic
induction
in Chapter
2 charge
total
electric
the
surface.
For
example,
11 m ). This
unit of If
area
unit
is called
the
weber
(1 Wb),
in
honor
ofant
Lei
de
Gauss
para
B
cos
f
=
1
happens
to
be
perpendicular
to
the
surface,
then
(magnetic
surface
B dA = 0
Theflux
SI unitthrough
of magnetic any
flux isclosed
equal
to the
unit of m
d£
B
o =magnetismo
physicist
Wilhelm
Weber
(1804–1891):
£
BA.
reduces
to
We
will
use
concept
of
magnetic
flux
exte
2the
face
encloses
an
electric
dipole,
the
total
electric
flux
is
zero
B
B
=
11
m
).
unit
of
area
This
unit
is
called
the
weber
(1
W
C
ingzero.
our study
of may
electromagnetic
induction
in
Chapter
29.!
dA
physicist
Wilhelm
Weber
(1804–1891):
charge
is
(You
want
to
review
Section
22.3
on
Gauss
2
#
hET: Magnet and Compass
S to the
S
S
1 Wb
= 1toTthemunit of magnetic field (1
The SI unit of magnetic flux
is equal
R
The particle therefore moves under the influence of a constant-m
F
=
where
is
the
mass
the
particle.
Solving
Eq.
(27.10)
for
(a) The
orbit ofm
a charged
particle
in aof
uniform
that is always
atpartículas
right angles toem
the velocity
of the
particle. Compar
Movimento
de
campos
magnéticos
magnetic
field
circular
we find
sion path,
of circular
motion in Sections
3.4 and 5.4, we see that the par
S
here
is
the
mass
of
the
particle.
Solving
Eq.
A charge m
moving
at
right
angles
to
a
uniform
B
circle, traced out with constant speed v. The centripetal accelerati
field
moves
insob
a circle
constant
speed
Movimento
açãoatde
forças
magnéticas
apenas
se dámass
sempre com
velocidade
where
m
is
the
of
the
particle
S only
the
magnetic
force
acts,
so
from
Newton’s
second
law,
S
mv
rcular
path,
weperpendicular
find
because
F and
v are always
to
constante
each other.
R =
S
v
(radius
ofwe
a circular
orbit in a magn
circular
path,
find
ƒqƒB
v2
mv
S
F = ƒ q ƒ vB = m
R
mv
R
=
p>
p = mvorbit
We canRalso
write
this
as
q
B,
where
is th
ƒ
ƒ
=
(radius
of
a
circular
S
where m isFthe mass of the particle.
for the
r
R = Solving Eq. (27.10)
(radius
of
raiosthe
parapartic
uma
q
particle’s
momentum.
If
the
charge
is
negative,
q
B
ƒ
ƒ
circular
path, we find
ƒqƒB
R
órbita circular
around the orbit in Fig. 27.17a.
The angularS speed
mvS v of the particle can be found from E
RF =
(radius of a circular orbit in a magnetic fi
v
Combining
this with
(27.11),
get
R = p>
We
can
R we
=write
p> ƒ qthis
pƒ
can
alsoS write
asalso
ƒ B, aswhere
ƒ q this
ƒ BEq.
We
P
F
particle’s
momentum.
Ifisthe
charge
q
article’s momentum.
If the
charge
negative
q
B
q
B
ƒ
ƒ
ƒ
ƒ
v
R
=
p>
p
=
mv
We can also
write
this
as
q
B,
where
is
the
ma
ƒ
ƒ
v
around
the
orbit
in
Fig.
27.17a.
v
=
=
=
v
O
round
the
orbit
in Fig.If27.17a.
B
particle’s
momentum.
the charge
themparticle m
mv
R q is negative,
The27.17a.
angular speed v of the part
around
the
orbit
in
Fig.
v
The angular
speed
of
the
particle
can
be
fo
The angular speed v of the particle can be found from Eq. (9
S
S
Combining
thistime
withis Eq.
we
ƒ = (27.11),
v>2p. This
per unit
The
number
of asrevolutions
(b) An
electron
beam (seen
a white arc)
parallel (vi) and perpendicular (v') to the
caso geral
magnetic Movimento
field, so it moves
in a helical path.
y
v'
S
v
vi
z
q
S
B
x
Visualzação de um feixe de elétrons
Garrafas magnéticas
and Magnetic Forces
ear
agion.
ed
of
rial
elts
ed
alis
f
S
S
v
B
S
v
S
B
+
S
F
I
S
F
I
S
F
Coil 1 1
Bobina
S
B
S
v
(b)
(a)
Charged particles
from sun enter earth’s
magnetic field
Protons trapped
in inner radiation
belts
Coil 22
Bobina
F
Coil 1
S
Coil 2
B
S
v
(b)
(a)
partículas
carregadas
Charged particles
sun enternoearth’s
dofrom
sol entram
magnetic
campo
mag.field
da Terra
prótons
presos nos
Protons trapped
cinturões
de radiação
in inner radiation
internos
belts
North
Pólo
Pole
Norte
Pólo
South
Sul
Pole
Magnetic forces on charged particles play an important role in studies of elementary particles. Figure 27.21 shows a chamber filled with liquid hydrogen and
area
A
using
the
on
the
wire
segment
is
then
length
l
of
conductor
with
cross-sectional
area
A
using
t
ing
charges
are
positive.
Later
we
itive.
Later
we’ll
see
what
happens
when
they
are
ne
magnética
sobre
um
condutor
com
corrente
nt
has
magnitude
S
edForça
in
Eqs.
(25.2)
and
(25.3)
of
Section
25.1.
The
S number
l
along
the
wire
in
th
S
used
in
Eqs.
(25.2)
and
(25.3)
of
Section
25.1.
The
numb
The
drift
velocity
is
upwar
v
d
ty
is
upward,
The
average
fo
v
B
.
27.6
Magnet
S perpendicular to
d
S
S
lume
is
;
a
segment
of
conductor
with
length
has
volum
n
l
S
S
velocidade
de
J
volume
is n; a segment ofcharge
conductor
with
length
vol
lS, has
SIlB
F
=
=
Drift velocity
is
directe
F
!
qv
:
B
d
!
dos
directed
to
the
left
shown
in
the
figure;
s
:arrasto
B
,
S as
mber
of
charges
equal
to
The
total
force
on
all
th
nAl.
F
F
=
1nAl21qv
B2
=
1nqv
A
Current
A
of chargeof charges equal B
d total force
number
toare
The
onSdall
nAl.perpendicular,
S
StheFmagnitu
transportadores
carriers
ar,
the
magnitude
of
the
force
is
F
=
qv
B.
de
carga
s segment
has
magnitude
d
this
segment
hasismagnitude
F
!
I
l
:
B
We
can
derive
an
expression
The
force
always
perpendicular
to
bo
What
makes
an
electric
S
an
expression
for
total
force
on
all
the
moving
c
vd the density
25.3)
the current
is
J
=
nqv
.
The
length
l dof
conductor
with
cros
d
F =F1nAl21qv
B2
=
1nqv
A21lB2
currents
(that
is,
whose
=
1nAl21qv
B2
=
1nqv
A21lB2
dsame dright-ha
d
direction
determined
by
the
S cross-sectional
l
ctor
with
area
A
using
the
same
la
used
in
Eqs.
(25.2)
and
(25.3)
forces on the moving cho
e
can
rewrite
Eq.
(27.16)
as
F
om
Eq.
(25.3)
the
current
density
is
J
=
nqv
.
The
produc
From
Eq.
(25.3)
the
current
density
is
J
=
nqv
.
The
prod
Figure
27.27
illustra
d
d
charge
(Fig.ofq27.26).
Hence
this
forceofcan
be
iseach
segment
of charg
cond
n; anumber
) and (25.3)
Sectionvolume
25.1. The
current-carrying
co
nt I,rent
so we
Eq. (27.16)
as
I, socan
werewrite
can rewrite
Eq.
(27.16)
as
ing-coil
galvanometer
t
number
of
charges
equal
to
nAl
ment
of
conductor
with
length
has
volume
and
l
Al
If
the
conductor
F
=
IlB
he
force
on
a
single
moving
charge.
We
rep
S
S
S
forces
on
conductors.
S
this
segment
has
magnitude
F
=
IlB
IlBall the moving
s equal to nAl. The total forceFF=on
gth inl aofcurrent-carrying
conductor with
cross-sectional
arge
conductor.
S
d
l
.
The
force
dF
on
We
can
compute
the
f
lfield
along
the
wire
in
the
direction
of
the
curre
S
S
Bnot perpendicular
is
not
perpendicular
the
wire
but
m
If
the
B
field
is
to
the
wire
but
makes
magnitude
F
=
1nA
If the B field isJ not perpendicular toto
the
wire
but
makes
an
netic force F ! qv : B
handle
the situation
theSsame
way
we
did
in
Section
27.
ndle
the
situation
the
same
way
we
did
in
Section
27.2
situation
the
same
way
we
did
in
Sectio
From
Eq.
(25.3)
the
current
den
S
S
S
S
S
S
S
F
=
1nAl21qv
B2
=
1nqv
A21lB2
Only
the
component
of
B
perpendicular
to
the
wire
(and
to
d
d
S
ly the F
component
of
B
perpendicular
to
the
wire
(and
to
t
dF
!
I
d
l
:
B
!
I
l
:
B
(magnetic
force
on
rent
I,
so
we
can
rewrite
Eq.
(27
the
charges)
exerts
a
force;
this
component
is
B
=
B
sin
omponent
of
B
perpendicular
to
the
wire
(
!
charges) exerts a force; this component is B! = B sin f.
S
S
S
S
S
• Magnitude is F 5 IlB! 5 IlB sin f.
S sobre um condutor com corrente
Força magnética
• Direction of F is given by the right-hand rule.
S
F
B' 5 B sin f
S
S
l
B
f
Bi
I
27.30 What
is
the
total
magnetic
force
on
the
conductor?
Força magnética num condutor curvo
y
dFy
S
dF
S
B (out)
S
dl
I
u
dl
S
F
R
I
L
L
I
du
S
u
O
dFx
x
I (in)
Teste seu entendimento
Which
Qual
orientation?
orientação?
A
B
r
Switch
chave
barraConducting
condutora
bar
trilhos
Conducting
condutores
rails
❙
😓😓
S
F
S
B
forces are reversed.
+
and
magnetic
fields
called
a
velo
he
forces
are
reversed
and
magnetic
fields
are
m,
charge
q,
and
speed
v
enters
a
region
of
space
where
v (a)
enters
a
region
of
space
where
the
electric
Aplicações:
seletor
de
velocidades
S
Schematic diagram of velocity selector
with
mass
m,
charge
q,
and
spee
ative.
The
electric
field
E
is
t
tic
fields
are
perpendicular
to
the
particle’s
velocity
and
to
lar to the
particle’s
velocity
and
to
each
other.
Fonte de partículas
S
S
S
figure.
If
q
is
positive,
and
magnetic
fields
are
perpendic
Source
of
charged
particles
carregadas
(b)
Free-body
diagram
for
a
positive
part
cmfield
E is to
thefield
left,Band
the magnetic
nd
the
magnetic
is into
the plane field
ofStheB is into the
of velocity
selector
the
magnetic
force
is
t
The
electric
field
E
is
to
the
left,
a
q
is
positive,
the
electric
force
is
to
the
left,
with
magnitu
force is to the left, with magnitude tudes
qE, and
Only
if for
a charged
E
and
B,
a
pa
figure.
If
q
is
positive,
the
electr
F
!
qE
F
!
qvB
particle
has
v
!
E
urce
of
charged
particles
E
B
ic
force
isS to theqvB.
right,
with
magnitude
qvB.
For
given
fi
with
magnitude
For
given
field
magniBy the right-hand
rule,
equal dointhemagnitude;
th
S
electric
and
ma
v
the
magnetic
force
is
to
the
right
the
force
of
the
B
field
de B,
a particular
value
of v theforces
electric
magnetic
fo
of for
v the
electric and
magnetic
willand
beline
straight
with
forces
cancel.
Allcon
othe
v
on
the
charge
points
to
tudes
E
and
B,
for
a
particular
val
S
particles
are
deflected
magnitude;
the Btotal
force
is then travels
zero,
and
-qE
qvB particle
= 0; solv
e is then zero,
and
the particle
in+ athe
the
right.
By the right-hand
rule,
equal
in
magnitude;
the
total
fo
S
S
find
ethewith
constant
velocity.
For
zero
total
force,
gF
=
y.
For
zero
total
force,
g
F
=
0,
we
need
S
y
E
y
force of the B field
The force straight
of the E field
line
with
constant
veloc
Bon=the0;v
solving
for
the
speed
v
for
which
there
is
no
de
speed
for points
which
there
is
no
deflection,
we
charge
to
on the charge points to
the right.
the left. - qE + qvB = 0; solving for the
find
S
The force
For a negative charge,
E
Only particles with spe
E of the E field
v of=both
v the
= charge points the
(27.13)
on
to directions
by
the
fields
(Fig.
27.22
B
forces are reversed.
the left.B
+
+
+
+
+
+
ticles having
a particul
27.23 Thomson’s
apparatus
for me
ingbeing
the
ratio
the
electron.bein
e/minforEq.
les
equal towithout
E>B can
pass
through
without
out
(27.13),
a ve
E>Bwith
canspeeds
pass through
deflected
electrons pass
straight
throughcharge:
the plates when Eq. (2
e eimpact.
is theThe
magnitude
of the
electron
fied; combiningexperimento
this with Eq. (27.14),
we get
27.5
Applications
Aplicações:
de Thompson
(elétron)
ur+
2
2eV
1
2
E
e
E
2eV
mv
=
eV
v
=
1
V
2=or Electrons
travel
fromdo
thecatodo
cathode
to the ascreen.
Elétrons
viajam
para
tela
so
=
2
gained kinetic energy 2 mv
lostAelectric
potential
2
m
B equals
A m + the feixe
m
2VB
de elétrons
Electron
beam
896
CHAPTER 27 Magnetic Field and Magnetic Forces
27.5
Applications of Motion
of Charged Particles
e is the magnitude of the electron charge:
tela ratio
Applications
of Mo
e>
All the quantities on the right sideB can be 27.5
measured,
soScreen
the
s pass
between
the
plates
P
and
P¿
and
strike
the
screen
27.5
Applications
of M
2eV
e
m
mass
can
be
determined.
It
is
not
possible
to
measure
or
sep
1
A
2
A"
P
mv
= eV
ormaterial
v = that fluoresces (glows)
(27.14)
Catodo
Cathode
2
ch is
coated
with
a
at
t
Anodes
method, only
their
ratio.
m
A
1
2anodos
P"
Eelectric
netic
energy
equals
the
lost
potential
mv
1
2
e>m
The
most
significant
aspect
of
Thomson’s
measurement
2
ctrons
pass
straight
through
the
plates
when
Eq.
(27.1
gained
energy
equals
the
lost
electric
potential
mv
Entrekinetic
as
placas
P
e
P'
existem
Between plates P and P" 2there
agnitude
of
the
electron
charge:
pass
between
the
plates
P
and
P¿
and
strike
the
screen
at
the
end
found
a
single
value
for
this
quantity.
It
did
not
depend
on
the
cat
campos
perpendiculares
e
–
are
mutually
perpendicular,
is thewith
magnitude
of the electron
charge:
ethis
Eq.
(27.14),
we
get
uniform
andagas
Bmaterial
fields.
E eE B.
h is uniformes
coated
with
(glows)
the point
of
the residual
in the that
tube,fluoresces
or anything
else at
about
the experime
2eV
ronspendence
pass
straight
through
the
plates
when
Eq.
(27.13)
is
satisshowed
that
the
particles
in
the
beam,
which
we
now
cal
2eV
1
2 or
2 (27.14)
=
eV
v
=
(27.14)
mv
=
eV
or
v
=
E (27.14),
e
E
2eV
his with
Eq.
we get
a 2common
constituent
of
all
matter.
Thus
Thomson
is
credited
wit
m
A
A m
so
=
=
covery
2
m
Bof a subatomic
A m particle, the electron.
2VB
2
E
e
E
2eV
e>m
The
most
precise
value
of
available
as
of
this
ass
between
the
plates
P
and
P¿
and
strike
the screen
at
thewriting
end is
en the plates
P
and
P¿
and
strike
the
screen
at
the
end
so
=
(27.15)
=
2
is
coated
with
a
material
that
fluoresces
(glows)
atpoint
the point
of
m
m
B
A
2VB
with
a
material
that
fluoresces
(glows)
at
the
of
11
e>m
sonsonpass
thestraight
right through
side can
be
measured,
so
the
ratio
o
e>m
=
1.7588201501442
*
10
C>kg
the plates when Eq. (27.13) is satistraight through the plates when Eq. (27.13) is satisThis section describes several applications of the principles introduced in this
chapter. Study them carefully, watching for applications of Problem-Solving
Strategy 27.2 (Section 27.4).
27.22 (a) A velocity selector for S
charged
particles uses perpendicular E and
S
B fields. Only charged particles with
v = E>B move through undeflected.
(b) The electric and magnetic forces on
a positive charge. The forces are reversed
if the charge is negative.
(a) Schematic diagram of velocity selector
Source of charged particles
q
S
v
+
S
S
+
S
+
E
+
S
B
By the right-hand
rule,
S
the force of the B field
on the charge points to
the right.
S
The force of the E field
on the charge points to
the left.
Velocity SelectorS
In a beam of charged particles produced by a heated cathode or a radioactive
material, not all particles move with the same speed. Many applications, however, require a beam in which all the particle speeds are the same. Particles of a
specific speed can be selected from the beam using an arrangement of electric
and magnetic fields called a velocity selector. In Fig. 27.22a a charged particle
with mass m, charge q, and speed v enters a region of space where the electric
and magnetic fields
are perpendicular to the particle’s velocity
and to each other.
S
S
The electric field E is to the left, and the magnetic field B is into the plane of the
figure. If q is positive, the electric
S force is to the left, with magnitude qE, and
the magnetic force is to the right, with magnitude qvB. For given field magnitudes E and B, for a particular value of v the electric and magnetic forces will be
equal in magnitude; the total force is then zero, and the particle travels in a
straight line with constant velocity. For zero total force, g Fy = 0, we need
- qE + qvB = 0; solving for the speed v for which there is no deflection, we
find
v =
+
+
+
For a negative charge,
the directions of both
forces are reversed.
(b) Free-body diagram for a positive particle
FE ! qE
Only if a charged
FB ! qvB particle has v ! E B
do the electric and magnetic
forces cancel. All other
v
particles are deflected.
/
27.23 Thomson’s apparatus for measuring the ratio e/m for the electron.
E
B
(27.13)
Only particles with speeds equal to E>B can pass through without being deflected
by the fields (Fig. 27.22b). By adjusting E and B appropriately, we can select particles having a particular speed for use in other experiments. Because q divides
out in Eq. (27.13), a velocity selector for positively charged particles also works
for electrons or other negatively charged particles.
Thomson’s e/m Experiment
In one of the landmark experiments in physics at the end of the 19th century,
J. J. Thomson (1856–1940) used the idea just described to measure the ratio of
charge to mass for the electron. For this experiment, carried out in 1897 at the
Cavendish Laboratory in Cambridge, England, Thomson used the apparatus shown
in Fig. 27.23. In a highly evacuated glass container, electrons from the hot cathode
are accelerated and formed into a beam by a potential difference V between the two
anodes A and A¿. The speed v of the electrons is determined by the accelerating
+
V
Electrons travel from the cathode to the screen.
+
Electron beam
Screen
S
B
A
Cathode
A"
Anodes
P
S
E
P"
rection
shown.sinOn
is perpendicular to(b)the current
>22
sin
= 1IBa21b
f2this side, B(27.22)
(a) f as
S on this
Força
e
torque
sobre
uma
espira
de
corrente
e90°,
force
side
has
magnitude
TheB
twoispairs
of
forces
acting
on
the
loop
cancel,
so
no
net
force
acts
on
the
loop.
in the plane of the loop, and the nor-
z
S
Screen
Electron beam
Electrons travel from the cathode to the screen.
S
S
S
to B
(Fig.
27.31b).
The
torque
is
zero
when
is
f
However, the forces on the a sides of the loop F
(F and
2F)
produce
a
torque
B
=
IaB
z
t 5 is
(IBa)(b
sinf) on
the
loop.
e loop
parallel
or
antiparallel
to
the
field
(Fig.
S
stable
because the but
torque
is
S the
e ! Fequilibrium
withythe position
same magnitude
opposite
direction
acts
on
I
y
B
slightly
from
this
position,
the
resulting
S
f
is
the
angle
frotated
the
loop,
as
shown
in
the
figure.
𝜙 ângulo
F!
I = 180°
between
a
vector
toward
The
position
is an
f
=
0°.
f
S
S
entre
o
vetor
S direction
normalwith
to the loop
ef displaced
sides
length
b
make
an
angle
190°
f2
with
the
B
B
m
x
slightly from this position,
normal
S theS loop S
and theàmagnetic
S
Fabout
these
the vectors
! F ¿; their magnitude SF¿ is
B 90° 2rotation
f F ¿ and
field.
espira
e B sides
mon
Figure
27.31
shows
f
= 180°.
I are
2F
f
S
rce on the loop is zero,mEq. (27.22) ffor the torque
27.7 Force and Torque on a Current Loop
903
27.7 Force and Torque on a Current Loop
903
(equal to the perpendicular distance from the rotation axis to the line of action of
perpendicular
from due
the rotation
to the
linemagnitude
of action of
sin f, sodistance
the(equal
force)to the
is 1b>22
the torque
to eachaxis
force
has
1b>22
sin
f,
the
force)
is
so
the
torque
due
to
each
force
has
F1b>22 sin f. If we use Eq. (27.21) for F, the magnitude of the net torquemagnitude
is
F1b>22 sin f. If we use Eq. (27.21) for F, the magnitude of the net torque is
t = 2F1b>22 sin f = 1IBa21b sin f2
(27.22)
t = 2F1b>22 sin
(27.22)
S f = 1IBa21b sin f2
The torque is greatest when f = 90°,
B is
S in the plane of the loop, and the norS
The
torque
is greatest
when f to
= B90°,
B 27.31b).
is in the The
planetorque
of theisloop,
and the
normal
to this
plane
is perpendicular
(Fig.
zero when
f is
S
to this
plane
perpendicular
to Bis (Fig.
27.31b).
The torque
zero
when
f is
or 180°
and
the is
normal
to the loop
parallel
or antiparallel
toisthe
field
(Fig.
0° mal
and the
the loop
is parallelposition
or antiparallel
thetorque
field (Fig.
0° or 180°
27.31c).
The value
a stable
equilibrium
becausetothe
is
f normal
= 0° is to
27.31c).
value the
stable slightly
equilibrium
because
torque is
f =loop
0° is
zero
there, The
and when
is arotated
fromposition
this position,
thethe
resulting
zero there,
when ittheback
looptoward
is rotated
from
this position,
the resulting
torque
tends and
to rotate
position
is an
f slightly
= 0°. The
f = 180°
torque equilibrium
tends to rotate
it back
toward fslightly
is an
= 0°. The
f = 180°
unstable
position;
if displaced
from position
this position,
the loop
unstable
equilibrium
position;
if
displaced
slightly
from
this
position,
the
loop
tends to move farther away from f = 180°. Figure 27.31 shows rotation about
tends
to
move
farther
away
from
Figure
27.31
shows
rotation
about
f
=
180°.
the y-axis, but because the net force on the loop is zero, Eq. (27.22) for the torque
the y-axis,
butchoice
because
the net force on the loop is zero, Eq. (27.22) for the torque
is valid
for any
of axis.
isThe
valid
for
any
choice
of
area A of the loop is axis.
equal to ab, so we can rewrite Eq. (27.22) as
The area A of the loop is equal to ab, so we can rewrite Eq. (27.22) as
(magnitude of torque on a current loop)
(27.23)
t = IBA sin f
(magnitude of torque on a current loop)
(27.23)
t = IBA sin f
The product IA is called the magnetic dipole moment or magnetic moment of
product
called
thesymbol
magnetic
dipole
moment
or magnetic moment of
IA iswe
theThe
loop,
for which
use the
Greek
letter mu):
m (the
the loop, for which we use the symbol m (the Greek letter mu):
m = IA
(27.24)
m = IA
(27.24)
It is analogous to the electric dipole moment introduced in Section 21.7. In terms
analogous
to the
electric
dipole
momentloop
introduced
in Section 21.7. In terms
of It
m,isthe
magnitude
of the
torque
on a current
is
of m, the magnitude of the torque on a current loop is
t = mB sin f
(27.25)
t = mB sin f
(27.25)
whereS f is the
angle between the normal to the loop (the direction of the vector
S
where
f isBthe
angle
between
normal
the loop
direction
of the vector
area
A2Sand
. SThe
torque
tends the
to rotate
thetoloop
in the(the
direction
of decreasing
area
A
2
and
B
.
The
torque
tends
to
rotate
the
loop
in
the
direction
of
decreasing
f—that is, toward its stable equilibrium position in Swhich the loop lies
in the
f
—that
is,
toward
its
stable
equilibrium
position
in
which
the
loop
in the
xy-plane perpendicular to the direction of the field B S
(Fig. 27.31c). A lies
current
xy-plane
perpendicular
to
the
direction
of
the
field
B
(Fig.
27.31c).
A
current
loop, or any other body that experiences a magnetic torque given by Eq. (27.25),
loop,called
or anya other
bodydipole.
that experiences a magnetic torque given by Eq. (27.25),
is also
magnetic
is also called a magnetic dipole.
F¿ = IbB sin190°
f
b sin f - f2 = IbB cos(c)
l to ab, so we can rewrite
Eq. (27.22) as
B
S
z (d
to
P
nes of action of both forces
lie along the y-axis.
f
m
I
eitude
totalof force
the
loop
is
zero
because
the
forces
on
opposite
sid
y
F!
B
torque on
on
a
current
loop)
(27.23)
2F
B
a
pairs.
I
E P"
S
Magnetic Torque: Vector Form
S
Torque:
WeMagnetic
can also define
a vectorVector
magneticForm
moment M with magnitude IA: This is shown
S
S
S
S
S
alsoThe
define
a vector
moment
with magnitude
IA:plane
This isofshown
in We
Fig.can
27.31.
direction
ofmagnetic
M is
defined
to beMperpendicular
to the
the
S
in Fig.
The
direction of
is defined to
be perpendicular
to the
plane
of the
loop,
with27.31.
a sense
determined
byMa right-hand
rule,
as shown in Fig.
27.32.
Wrap
with
sense
determined
by a the
right-hand
rule,
Fig.direction
27.32. Wrap
theloop,
fingers
ofayour
right
hand around
perimeter
of as
theshown
loop ininthe
of
fingersThen
of your
right
hand
around
the perimeter
of the loop
in the
direction
of
thethe
current.
extend
your
thumb
so that
it is perpendicular
to
the
plane
of
the
S
S
the its
current.
Then
your thumb
so that
it isvector
perpendicular
to
the
plane
of
the
loop;
direction
is extend
the direction
of
M
(and
of
the
area
A
of
the
loop).
The
S
S
S
S
loop;isits
direction
is the
direction
of M (and of the vector area
A ofthey
the loop).
The
torque
greatest
when
M and
B are
when
are parS perpendicular and is zero
S
S
S is zero when they are partorque
is
greatest
when
M
and
B
are
perpendicular
and
B are
allel or antiparallel. In the stable equilibrium position, M and
S parallel.
S
S
allel
or antiparallel.
In thethis
stable
equilibrium
position,
and B vector
are parallel.
T, Swhich
Finally,
we can express
interaction
in terms
of theMtorque
T, which
Finally,
we
can
express
this
interaction
in
terms
of
the
torque
vector
we used for electric-dipole interactions in SectionS 21.7. From Eq. (27.25)
the
S
S
we
used
for
electric-dipole
interactions
in
Section
21.7.
From
Eq.
(27.25)
the
M
:
B
,
magnitude of T is
equal
to
the
magnitude
of
and
reference
to
Fig.
27.31
S
S
S
T
M
:
B
,
magnitude
of
is
equal
to
the
magnitude
of
and
reference
to
Fig.
27.31
shows that the directions are also the same. So we have
shows that the directions are also the same. So we have
S
–
B
S
+
S
I
Sof
gnetic dipole moment or magnetic moment
S
2F!
b
2F
mbol
(the
Greek
letter
mu):
m
net force on a current loop in a uniform magnetic field is zero. Howe
orque
not in general equal to zero.
m =is IA
(27.24)
S
S
S
27.32 The right-hand rule determines
the27.32
directionThe
of the
magneticrule
moment
of a
right-hand
determines
current-carrying
This is also
the of a
the direction ofloop.
the magnetic
moment
S
direction
of the loop’s
area
vector
A; S
current-carrying
loop.
This
is also
the
S
S
M!
vector
equation.
IA isS aof
direction
the loop’s
area vector A;
S
M ! IA is a vector equation.
I
I
I
I
S
m
S
m
S
A
S
A
I
I
I
I
greatest when they are antipara
S This isS
rrent-carrying loop.
also the
S
The
torque
is m
m
The
product
is
called
the
magnetic
dipole
moment
or
IA
Finally,
we
can
express
this
intera
of
the
loop
(F
and
2F)
produce
a
torque
U
as
a
function
of
orientatio
rection of the loop’s
area vector Ae
; energia potencial numa
B
S
Torque
espira
when letter
f 5 90°
(
z
use
the
symbol
(the
Greek
m
m
! IA is a vector equation.the loop, for which we
F
we used
for electric-dipole
interacti
between
the
electric
and
magn
the
plane
of the
S
S
I
T
magnitude
of
is
equal
to
the
magni
IA
dipoleI inSman=electric
field is T !
y
B
I
x (direc
showssponding
that the directions
are
also
theU
potential
energy
is
It is analogous to the electric dipole moment introduced
inSS
S
S
m
I
is loop
T S! isM : B,
S
of m, the magnitude of the magnetic
torque onSS
afield
current
S
S
netic field. AB
BT ! M : B
(vec
m
sponding potential
energy
is
x
I
S
S
S
S
I
S
B (b)
90° 2 f
f
.
f
f
y
I
S
F
t = mB sin f
#
This
resultthe2F
isnormal
directly
analogous
to
t
S
where
f
is
the
angle
between
to
the
loop
(the
di
S
S
z
S
S
Uexerted
= - MbyBan=electric
- mB cos
fE o
torque
field
area A2 and B. The torque tends to rotate the loop in the dir
(c)
b sinS f
The
torque
is
maximal
S
is, toward its stable
equilibrium
position
in Swhich
B f—that
z
(direction
normal
S
when f 5 90° (so B is in
With
this
definition,
U
is
zero
w
F
Potential
Energy
for
a
Magne
to
loop)
xy-planetheperpendicular
to
the
direction
of
the
field
B
(Fig
Th
plane of the loop).
S
m
to
the
magnetic
field.
f5
loop,
or
any
other
body
that
experiences
a
magnetic
torque
g
SI
S
When
a
magnetic
dipole
changes
ori
S
I B
S
B
fS 5
y(direction
F! normal
S
Sto loop)B
is also called axmagnetic
dipole.
work onBit. In an infinitesimal
F angula
I
S
Magnetic Torque:
x Bi
Loops
pla
I
Magnetic
Torque:
Vector
Form
I
S
m The collection of rectangles
7.33
Although
we haveS derived Eqs
S
2F!
I
S
S
B
b
The
Smagnitu
can also
define
a vector
magnetic
moment
M
with
xactly matchesS theWe
irregular
plane
loop
in 2F
loop,
all these relationships
are
2F!
S
libr
2F
he limit as the number
of rectangles
in Fig.
27.31. The directionnar
of M
is defined
to approximated
be perpendicul
loop
may be
in u
pproaches infinity loop,
and the
width
of each
with
a sense
determined by a right-hand rule, as shown
(c)
rectangular loops, as shown wh
in
27.34
The torque
T ! on
M :the
B on
this
nof
exactly matches
the irregular
loopthe
in sum
magnetic
field isplane
simply
of
the
torques
individual
loop,
all
these
relationships
are
valid
solenoid in a uniform magnetic field is
he
limit
as
the
number
of
rectangles
is
noid with N turns in a uniform
field
B,may
the
magnetic
is
nar
loop
be
directed
straight
into
theapproximated
page. Anmoment
actual as clo
approaches infinity and the width of each
solenoid
has many
more turns,
wrapped
rectangular
loops,
as
shown
in Fig. 27
rectangle approaches zero.
wh
closely
together.
t
=
NIAB
sin
f
al
in the same clockwise sense, then thefief
S
d
A planar current loop
adjacent to each other mcancel, and the
I
gr
any shape
be
where f isofthe
anglecanbetween
the
axis
of
the
solenoid
and
th
f the boun
are
due
to
currents
around
wh
S
approximated by a
field. The magnetic
moment
vector
M
is
along
the
solenoid
a
valid for aS plane current loop of anyin
set of rectangular
I
S
greatest when loops.
the solenoid axis
is
perpendicular
to
the magne
so
by M ! IA.
Torque: espiras e bobinas
when they are parallel. The effect
this
is tothis
tend
to r
Weofcan
alsotorque
generalize
whole
ne
I
loops
close
together;
the
effect
is
sim
into
a
position
where
its
axis
is
parallel
to
the
field.
Solenoids
I
t
is
moment,
the torque,
and the28.
potential
sources of magnetic field, as we’ll
discuss
in Chapter
lar
An
arrangement
of
particular
inte
The d’Arsonval galvanometer, described in Section 26.3, ma
to
wire, such as a coil wound on a circul
cot
netic torque on a coil carrying a current.
As
Fig.
26.14
shows,
I
closely
spaced, the solenoid
can be pr
ap
B
is not uniform
but is radial, solying
the side
thrusts
on
the
coil
are
al
I
in planes at right angles to its cu
lo
Thef
torque
to(27.28)
make the solenoid
rotate 90°,
lar to its plane. Thus the angle
in tends
Eq.
is always
re
magnetic
field
is
simply
the
sum
of
the
O torque
tende in
a fazer
o solenóide
em
S
clockwise
the plane
of the page,girar
aligning
S
S
de
is directly
to
the
current,
no
matter
what
the
27.34 torque
The torque
T ! M : proportional
B on this
noid
with
N
turns
in
a
uniform
field
B
magnetic
moment
m
with
field
B.
sentido horário no plano da figura, alinhando
solenoid coil.
in a uniform
magnetic
field
is
A restoring torque oproportional
to
the
angular
displacem
directed straight into the page. An actual momento magnético 𝜇 com o campo B. t =ma
by two
which also serve as current leads
solenoid provided
has many more
turns,hairsprings,
wrapped
of
S
S
S
S
where f is the angle between the ax
MAGNETIC FORCES
Introdução
Imageamento por ressonância nuclear
permite o exame dos tecidos moles do
pé que não são visíveis por raios X. No
entanto os tecidos moles não são
magnéticos. Como a técnica de RMN
funciona?
O paciente é colocado em um campo magnético de 1.5 T (10000 x o campo da
Terra) . O núcleo de cada átomo de hidrogênio no tecido a ser examinado possui um
momento de dipolo magnético que o alinha ao campo aplicado. A seguir o tecido é
iluminado com ondas eletromagnéticas que retiram o átomo do alinhamento. A
absorção de ondas eletromagnéticas é proporcional à quantidade de hidrogênio
presente. Como o osso tem menos hidrogênio, o tecido mole fica "iluminado". Essa
técnica é ideal para análise de tecidos humanos que não são visíveis em imagens de
raios X.
on in Fig. 27.39a.
Brushes are aligned with commutator
ow be (a)
in its
equisegments.
ation. But here’s
de rotação
contact with both Eixo
Rotation
axis
v Rotor
rotor
nce between the
Rotor has turned 90°.
Motor de corrente(b)contínua
v
I50
S
BI
S the rotor ends are attached
N
oop that is freeN to rotate
about
an
axis;
IS
es are colored red andt blue for clarity.) The commutator
escova
Brush
°.
I
v
S
m
comutador
(c) RotorCommutator
has
turned 180°.
I
+
t50
B
I
S
I
I
I
m50
S
t50
+
v
• Current flows into the red side of the
rotor
S
BI
S and out of the blue Nside.
S
I causes the
• Therefore the magnetic torque
S
t
rotor to spin counterclockwise.
S
S
m
m50
S
S
S
I
I
+
• Each brush is in contact with both
commutator segments, so the current
bypasses the rotor altogether.
• No magnetic torque acts on the rotor.