Download FACTORING GUIDE

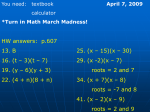
FACTORING GUIDE
I. Check for GCF
II. Count the number of terms
________________________________________________________________________________
Two Terms
1. Difference of squares
2. Sum or difference of cubes
A 2 B 2 = ( A B)( A + B)
A 3 B 3 = ( A B)( A 2 + AB + B 2 )
A 3 + B 3 = ( A + B)( A 2 AB + B 2 )
Example:
4 x 2 25 y 2 = (2 x 5 y )(2 x + 5 y )
A=2x B=5y
Examples:
x 3 8 = ( x 2)( x 2 + 2 x + 4)
A=x B=2
27 y 3 + 64 z 3 = (3 y + 4 z )(9 y 2 12 yz + 16 z 2 )
A=3y B=4z
*Note: A 2 + B 2 does NOT factor
________________________________________________________________________________
Three Terms
1.Leading Coefficient is 1
a) x 2 + x 6 = ( x + 3)( x 2)
(find 2 numbers that multiply out to
– 6 and add up to 1)
b) x 2 + 9 x + 14
(find 2 numbers that multiply out to
14 and add up to 9)
2. Leading Coefficient is NOT 1
a) Check to see if it is a perfect square trinomial
(use square root of first and last term as first guess
in trial and error)
4 x 2 20 xy + 25 y 2 = (2 x 5 y )(2 x 5 y )
= (2 x 5 y ) 2
b) Use trial and error to factor
(nail down your first and last terms and try
different combinations to get your outer and
inner terms to equal your original middle term)
2 x 2 5 x 12 = ( 2 x + 3)( x 4)
(outers = – 8x, inners = 3x, their sum is – 5x )
2 x 2 + 23 x 12 = (2 x 1)( x + 12)
(outers = 24x, inners = – 1x, their sum is 23x )
c) An alternative to trial and error is the “ac
method “
See textbook or a Math Center tutor for an
explanation.
_________________________________________________________________
Four Terms
Factor by grouping
Examples:
1. Two by Two:
2ax + 2ay 5 x 5 y = 2a ( x + y ) 5( x + y ) = ( x + y )(2a 5)
x 3 3 x 2 + 5 x 15 = x 2 ( x 3) + 5( x 3) = ( x 3)( x 2 + 5)
2. Three by one:
x 2 6 x + 9 y 2 = ( x 3) 2 y 2 = ( x 3 y )( x 3 + y )