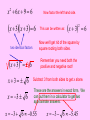Download P.5+Revised Factoring

FACTORING
POLYNOMIALS
15 5x
The first thing we do when factoring is to see if there is a
common factor. We could factor out a 5 here or a –5.
Let's factor out a -5.
Yes---it checks!
 5(3  x)  15
15 5x
Remember you can always check to see if you've
done this step correctly by re-distributing through.
Let's check it.
Binomial Expression
Is the expression a difference of
two perfect squares
a) Is the first term a perfect square?
b) Is the last term a perfect square?
c) Is it the difference? (- sign in the middle)
Factor
Completely:

20 y  45
2
5 4y 9
2


Two terms left----is it the difference of
squares?
5 2 y   3
2
Look for something in
common (there is a 5)
2

Yes---so factor into
conjugate pairs.
52 y  32 y  3
Factoring Trinomials
Remember a trinomial is a polynomial with three terms.
To factor them what we are doing is "unFOILing" so let's
look at one we've FOILed and see how we can reverse
the process.
x·x
 x  2 x  4
-8 · 1
-1 · 8
-2 · 4
-4 · 2
 x  2x  8
2
This term came from multiplying last
first
terms last
outers
times
together
andso
inners
wesoneed
and
we must
to
then
see
figure
combining
whatout
2in
like terms.
factors
that(we'll
would
willgive
multiply
figure
us -8.
how
toWhich
give
to get
usofitxthese
a minute).
would
add up to the middle's coefficient?
( x - 2 )(
x + 4)
A perfect square trinomial is one that can be factored into
two factors that match each other (and hence can be
written as the factor squared).
x  12 x  36  x  6x  6  x  6
2
2
This is a perfect square trinomial because it factors into
two factors that are the same and can be written as the
factor squared.
Notice that the first and last terms are perfect squares.
The middle term comes from the outers and inners when
FOILing. Since they match, it ends up double the product of
the first and last term of the factor.
Factor by Grouping
4u  6u  2u  3
4
3
When you see four terms, it is a clue to try factoring by
grouping. Look at the first two terms first to see what is in
common and then look at the second two terms.

 

2u 2u  3  1 2u  3
3
3
These match so let's factor them out
2u
3

 3 2u  1
There is nothing in common in the second two terms but we
want them to match what we have in parenthesis after
factoring the first two terms so we'll factor out a -1
Summary of How to Factor a Polynomial
1. Look for something in common
Before you try anything else, see if you can factor out anything
2. Look at the number of terms
a) Two terms
Is it the difference of squares (that factors into conjugate pairs?)
Is it the sum or difference of cubes
b) Three terms – trinomial factoring (unFOILing)
c) Four terms – try factoring by grouping
8m n  20m n  48mn
3
2
Look for something in common

3
There is a 4mn in each term
4mn 2m  5mn  12n
2
2
2

Three terms left---try
trinomial factoring
Check by FOILing and then
distributing 4mn through
"unFOILing"
4mn2m  3nm  4n
-3mn
8mn
5mn
Completing the Square
What are we going to do if we have non-zero values for
a, b and c but can't factor the left hand side?
x  6x  3  0
2
x  6 x  3
2
This will not factor so we will complete the
square and apply the square root method.
First get the constant term on the other side by
subtracting 3 from both sides.
9  3  ___
9
x  6 x  ___
2
x  6x  9  6
2
Let's add 9. Right now we'll see that it works and then we'll look at how
to find it.
We are now going to add a number to the left side so it will factor
into a perfect square. This means that it will factor into two
identical factors. If we add a number to one side of the equation,
we need to add it to the other to keep the equation true.
x  6x  9  6
2
Now factor the left hand side.
x  3x  3  6
x  3
 x  3
2
6
Now we'll get rid of the square by
square rooting both sides.
two identical factors
2
This can be written as:
Remember you need both the
positive and negative root!
 6
x3  6
Subtract 3 from both sides to get x alone.
x  3  6
These are the answers in exact form. We
can put them in a calculator to get two
approximate answers.
x  3  6  0.55
x  3  6  5.45
Okay---so this works to solve the equation but how did we
know to add 9 to both sides?
9  3  ___
9
x  6 x  ___
2
x  3x  3  6
+3x
+3 x
6x
We wanted the left hand side to factor
into two identical factors.
When you FOIL, the outer terms and the
inner terms need to be identical and need
to add up to 6x.
The
termterm's
in the coefficient
original trinomial
willby
then
be the
middle
the last
middle
divided
2 and
squared
term's coefficient divided by 2 and squared since last term
times last term will be (3)(3) or 32.
So to complete the square, the number to add to both sides
is…
Let's solve another one by completing the square.
2 x  16 x  2  0
2
2
2
2
To complete the square we want the coefficient
of the x2 term to be 1.
2
x 2  8x  1  0
Divide everything by 2
16  1  ___
16
x 2  8x  ___
 8


 2 
Since it doesn't factor get the constant on the
other side ready to complete the square.
2
 16
So what do we add to both sides?
the middle term's coefficient divided by 2 and squared
x  4x  4  x  42  15
2
x  4   15
x  4   15
Factor the left hand side
Square root both sides (remember )
Add 4 to both sides to
get x alone
x  4  15
Quadratic Formula
By completing the square on a general quadratic equation in
standard form we come up with what is called the quadratic formula.
(This is derived in your book on page 101)
ax  bx  c  0
2
 b  b 2  4ac
x
2a
This formula can be used to solve any quadratic equation
whether it factors or not. If it factors, it is generally easier to
factor---but this formula would give you the solutions as well.
1x
2
 6x  3  0
We solved this by completing the square
but let's solve it using the quadratic formula
 6  36  12
(1) (3) 
 b6  b6 2  4ac
x
2
(1)
2a
Don't make a mistake with order of operations!
Let's do the power and the multiplying first.
24  4  6  2 6
 6  36  12  6  24  6  2 6
x


2
2
2

2 3 6

2

There's a 2 in common in
the terms of the numerator
 3  6
These are the solutions we
got when we completed the
square on this problem.
NOTE: When using this formula if you've simplified under the
radical and end up with a negative, there are no real solutions.
(There are complex (imaginary) solutions, but that will be dealt
with in the next section).
SUMMARY OF SOLVING QUADRATIC EQUATIONS
Get the equation in standard form:
ax  bx  c  0
2
If there is no middle term (b = 0) then get the x2 alone and square
root both sides (if you get a negative under the square root there are
no real solutions).
If there is no constant term (c = 0) then factor out the common x
and use the zero-product property to solve (set each factor = 0)
If a, b and c are non-zero, see if you can factor and use the zeroproduct property to solve
If it doesn't factor or is hard to factor, use the quadratic formula to
solve (if you get a negative under the square root there are no real
solutions).