Download Lecture 11. Power in Electric Circuits, Kirchhoff`s Rules

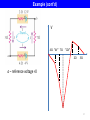
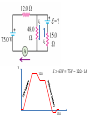
Lecture 11. Power in Electric Circuits, Kirchhoff’s Rules
Outline:
Energy and power in electric circuits.
Voltage and Current Sources.
Kirchhoff’s Rules.
Lecture 10:
Connection of resistors in parallel and in series.
Batteries: the potential energy of charge carriers is increased by non𝑉𝑎𝑎 = ℰ − 𝐼𝐼
electrostatic (non-conservative) forces.
Non-ideal batteries: internal resistance.
Potential distribution around a complete circuit.
1
The second common hour in Physics 227 will be held Thursday, November 12 from 9:50 to
11:10 PM at night in 4 locations on two campuses, Livingston and Busch. You should go to
the exam location assigned to the first letters of your last name. Note that the exam
locations have changed since the first exam. Make sure you go to the correct exam
location where you will find your exam.
Aaa-Gzz
Haa-Mzz
Naa-Shz
Sia-Zzz
BE Aud
LSH Aud
PHY LH
SEC 111
If you have a conflict for this exam you must send your request for a conflict and your
entire schedule for the week of November 8 to Professor Cizewski
[email protected] no later than 5:00 PM on Wednesday, November 4. If you
do not request a conflict exam before the deadline you will have to take the exam as
scheduled on November 12.
Energy and Power in DC Circuits
Each charge carrier going “downhill” from a
higher 𝑉𝑎 to a lower 𝑉𝑏 dissipates the energy
𝑒𝑉𝑎𝑎 in its environment: the gained kinetic
energy is transformed into thermal energy
(“heat”) due to inelastic scattering
(remember, no acceleration!).
If charge 𝑑𝑑 passes a circuit element in
𝑑𝑑, the power generated is:
For a resistor R:
2
𝑉
𝑃 = 𝑉𝑉 = 𝑅𝐼 2 =
𝑅
𝑃=
𝑑𝑞𝑉𝑎𝑎
= 𝑉𝑎𝑎 𝐼
𝑑𝑑
- Joule (resistive)
heating power
Units: 1J/1s =1Watt (W)
3
Problem
What is the maximum power one can get
(dissipate in the load) from a given (ℰ, 𝑟) battery?
𝑉
ℰ =𝐼 𝑟+𝑅
𝑃=
𝑃
“current” source
r>>R
𝑑𝑑
1
∝
𝑑𝑑
𝑟+𝑅
−2
2
𝑟 + 𝑅 − 2𝑅 = 0
𝑅
𝑟+𝑅
𝑅𝐼2
∝𝑅
3
𝑅=𝑟
=0
𝑅
=
𝑟+𝑅
𝑟
2
ℰ
2
“voltage” source
r<<R
∝ 1/𝑅
𝑅
𝑃𝑚𝑚𝑚 → @ 𝑅 = 𝑟
6
Light Bulbs
The incandescent light bulb: a resistor, being heated by current,
emits black-body radiation in the visible wavelength range.
Bulbs are rated by power. Resistance of a 60W bulb designed for
120V (neglect the fact that this rating is for the AC (not DC)
current):
𝑉2
120𝑉 2
𝑅=
=
= 240Ω
𝑃
60𝑊
Note that a light bulb that is rated at 60W actually produces
only about 3 W of visible light 
The larger the power, the smaller the resistance (we assume that R is much greater
than the internal resistance of the voltage source).
𝑃
The wall outlet 110V can be considered as a
voltage source – the internal resistance is
smaller than all typical loads.
∝𝑅
𝑟
∝ 1/𝑅
𝑅 (𝑟 is fixed)
7
Kirchhoff’s Junction Rule
Junction Rule (for currents): charge conservation
� 𝐼𝑖 = 0
𝑖
Currents flowing in →
+
Currents flowing out →
-
14
Kirchhoff’s Loop Rule
𝑟
𝑉
ℰ
𝑅
ℰ
Loop Rule (energy conservation):
� ℰ𝑖 + � 𝑉𝑖 = 0
𝑖
𝑖
for any
closed
loop
� 𝑉𝑖 = 0
𝑖
𝐼𝐼
𝐼𝐼
𝑥
if we neglect the difference
between 𝑉’s and ℰ’s, and
accept the sign conventions.
15
Example
We don’t need to know a priori the actual
direction of the current: if we get the negative
value of I, that would mean that the current
flows in the direction opposite to the
direction of “travel”.
� ℰ𝑖 + � 𝑉𝑖 = 0
𝑖
𝑖
−4𝑉 + 12𝑉 − 𝐼 7Ω + 2Ω + 3Ω + 4Ω = 0
8𝑉
𝐼=
= 0.5𝐴
16Ω
16
Example (cont’d)
V
4Ω “4V” 7Ω “12V”
2Ω
3Ω
a – reference voltage =0
17
More Examples
6Ω
3Ω
(a)
3Ω
3Ω
6Ω
36𝑉
𝐼=
= 4𝐴
9Ω
Problem 26.77:
(a) what is the potential difference Vab when the switch
is open?
(b) What is the current through the switch when the
switch is closed?
(c) What is the equivalent resistance when the switch is
closed?
𝑉𝑎 = 36𝑉 − 6Ω ∙ 4𝐴 = 12𝑉
𝑉𝑏 = 36𝑉 − 3Ω ∙ 4𝐴 = 24𝑉
𝑉𝑎 − 𝑉𝑏 = 12𝑉 − 24𝑉 = −12𝑉
20
More Examples (cont’d)
6Ω
3Ω
3Ω
3Ω
ℰ
6Ω
1
Problem 26.77:
(b) What is the current through the switch when
the switch is closed?
(b)
loop 1: 36 − 6 ∙ 𝐼1 − 3 ∙ 𝐼1 − 𝐼3 = 0
loop 2: −6 ∙ 𝐼1 − 3 ∙ 𝐼3 + 3 ∙ 𝐼2 = 0
2
3
𝐼1 =
36
10.5
Choose (arbitrary) directions of currents and
travel along the loops. Note that the “current”
rule has been taken care of.
loop 3: −3 ∙ 𝐼1 − 𝐼3 + 6 ∙ 𝐼2 + 𝐼3 + 3 ∙ 𝐼3 = 0
+
𝐼3 = 𝐼2 − 2𝐼1
(from Eq.2)
−3 ∙ 𝐼1 + 12 ∙ 𝐼3 + 6 ∙ 𝐼2 = 0
(from Eq.3)
−3 ∙ 𝐼1 + 12 ∙ 𝐼2 − 24 ∙ 𝐼1 + 6 ∙ 𝐼2 = 0
3
𝐼2 = 𝐼1
2
36 − 6 ∙ 𝐼1 − 3 ∙ 𝐼1 + 3 𝐼2 − 2𝐼1 = 36 − 10.5 ∙ 𝐼1 = 0
3
𝐼3 = 𝐼1 − 2𝐼1 = −0.5𝐼1
2
𝐼3 = −
18
= −1.71
10.5
“-” means that our initial direction of I3 has to be reversed.
21
More Examples (cont’d)
6Ω
3Ω
3Ω
3Ω
6Ω
Problem 26.77:
(a) what is the potential difference Vab when the switch
is open?
(b) What is the current through the switch when the
switch is closed?
(c) What is the equivalent resistance when the switch is
closed?
(c)
ℰ
1
2
3
𝑰
+
𝐼1 =
𝑅𝑒𝑒
ℰ
=
𝐼
𝐼 = 𝐼1 + 𝐼2
36
10.5
3
𝐼2 = 𝐼1
2
𝑅𝑒𝑒 =
𝐼 ≈ 8.6𝐴
36𝑉
= 4.2Ω
8.6𝐴
22
Conclusion
Resistors in Series and Parallel
Voltmeters and Ammeters
Kirchhoff’s Rules
Next time: Lecture 12: RC circuits
§§ 26.4
23
Voltmeters
The goal: to measure the voltage difference across
an element (ideally, without affecting the circuit due
to the voltmeter connection).
V
𝑹𝒊𝒊
An ideal voltmeter:
A. has 𝑹𝒊𝒊 = 𝟎 and should be connected in parallel with
the circuit element being measured.
𝑹
V
𝑹
𝑹𝒊𝒊
B. has 𝑹𝒊𝒊 = 𝟎 and should be connected in series with
the circuit element being measured.
C. has 𝑹𝒊𝒊 = ∞ and should be connected in parallel
with the circuit element being measured.
D. has 𝑹𝒊𝒊 = ∞ and should be connected in series with
the circuit element being measured.
24
Voltmeters
The goal: to measure the voltage difference across
an element (ideally, without affecting the circuit due
to the voltmeter connection).
V
𝑹𝒊𝒊
An ideal voltmeter:
A. has 𝑹𝒊𝒊 = 𝟎 and should be connected in parallel with
the circuit element being measured.
𝑹
V
𝑹
𝑹𝒊𝒊
B. has 𝑹𝒊𝒊 = 𝟎 and should be connected in series with
the circuit element being measured.
C. has 𝑹𝒊𝒊 = ∞ and should be connected in parallel
with the circuit element being measured.
D. has 𝑹𝒊𝒊 = ∞ and should be connected in series with
the circuit element being measured.
Voltmeter: high internal resistance
25
Ammeters
The goal: to measure the current in a circuit element
(ideally, without affecting the current due to the
ammeter connection).
I
𝑹𝒊𝒊
An ideal ammeter:
A. has 𝑹𝒊𝒊 = 𝟎 and should be connected in parallel with
the circuit element being measured.
𝑹
I
𝑹
𝑹𝒊𝒊
B. has 𝑹𝒊𝒊 = 𝟎 and should be connected in series with
the circuit element being measured.
C. has 𝑹𝒊𝒊 = ∞ and should be connected in parallel
with the circuit element being measured.
D. has 𝑹𝒊𝒊 = ∞ and should be connected in series with
the circuit element being measured.
26
Ammeters
The goal: to measure the current in a circuit element
(ideally, without affecting the current due to the
ammeter connection).
I
𝑹𝒊𝒊
An ideal ammeter:
A. has 𝑹𝒊𝒊 = 𝟎 and should be connected in parallel with
the circuit element being measured.
𝑹
I
𝑹
𝑹𝒊𝒊
B. has 𝑹𝒊𝒊 = 𝟎 and should be connected in series with
the circuit element being measured.
C. has 𝑹𝒊𝒊 = ∞ and should be connected in parallel
with the circuit element being measured.
D. has 𝑹𝒊𝒊 = ∞ and should be connected in series with
the circuit element being measured.
Ammeter: low internal resistance
27
Appendix 1: Built-in Battery Tester
Bi-layer structure: the thermochromic (non-conductive)
ink deposited on top of the conductive ink.
𝑅𝑒𝑒
𝑉
𝑟
1
1
1
=
+
+
𝑅1 𝑅2 𝑅3
𝐼=
ℰ
𝑟 + 𝑅𝑒𝑒
𝑉𝑎𝑎 2
𝑃1 =
𝑅1
−1
𝑉𝑎𝑎
=
𝑅1 𝑅2 𝑅3
𝑅1 𝑅2 + 𝑅1 𝑅3 + 𝑅2 𝑅3
𝑅𝑒𝑒
= ℰ − 𝐼𝐼 = ℰ
𝑟 + 𝑅𝑒𝑒
𝑉𝑎𝑎 2
𝑃2 =
𝑅2
𝑉𝑎𝑎 2
𝑃3 =
𝑅3
∆T of the thermochromic ink is proportional to P/area:
(e.g., 𝑃3 is ~2 times smaller than 𝑃1 , and its area is 2 times greater)
𝑃1 𝑃2 𝑃3
: :
= 4: 2: 1
𝐴1 𝐴2 𝐴3
28
𝐼1
𝐼2
V
12Ω
ℰ > 63V = 75V − 12Ω ∙ 1𝐴
15Ω