* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture 11. Power in Electric Circuits, Kirchhoff`s Rules
Schmitt trigger wikipedia , lookup
Lumped element model wikipedia , lookup
Operational amplifier wikipedia , lookup
Power electronics wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Index of electronics articles wikipedia , lookup
Flexible electronics wikipedia , lookup
Distributed element filter wikipedia , lookup
Regenerative circuit wikipedia , lookup
Integrated circuit wikipedia , lookup
Power MOSFET wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Two-port network wikipedia , lookup
Current source wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Current mirror wikipedia , lookup
Yagi–Uda antenna wikipedia , lookup
Surge protector wikipedia , lookup
Opto-isolator wikipedia , lookup
RLC circuit wikipedia , lookup
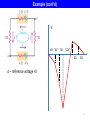
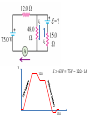
Lecture 11. Power in Electric Circuits, Kirchhoff’s Rules Outline: Energy and power in electric circuits. Voltage and Current Sources. Kirchhoff’s Rules. Lecture 10: Connection of resistors in parallel and in series. Batteries: the potential energy of charge carriers is increased by non𝑉𝑎𝑎 = ℰ − 𝐼𝐼 electrostatic (non-conservative) forces. Non-ideal batteries: internal resistance. Potential distribution around a complete circuit. 1 The second common hour in Physics 227 will be held Thursday, November 12 from 9:50 to 11:10 PM at night in 4 locations on two campuses, Livingston and Busch. You should go to the exam location assigned to the first letters of your last name. Note that the exam locations have changed since the first exam. Make sure you go to the correct exam location where you will find your exam. Aaa-Gzz Haa-Mzz Naa-Shz Sia-Zzz BE Aud LSH Aud PHY LH SEC 111 If you have a conflict for this exam you must send your request for a conflict and your entire schedule for the week of November 8 to Professor Cizewski [email protected] no later than 5:00 PM on Wednesday, November 4. If you do not request a conflict exam before the deadline you will have to take the exam as scheduled on November 12. Energy and Power in DC Circuits Each charge carrier going “downhill” from a higher 𝑉𝑎 to a lower 𝑉𝑏 dissipates the energy 𝑒𝑉𝑎𝑎 in its environment: the gained kinetic energy is transformed into thermal energy (“heat”) due to inelastic scattering (remember, no acceleration!). If charge 𝑑𝑑 passes a circuit element in 𝑑𝑑, the power generated is: For a resistor R: 2 𝑉 𝑃 = 𝑉𝑉 = 𝑅𝐼 2 = 𝑅 𝑃= 𝑑𝑞𝑉𝑎𝑎 = 𝑉𝑎𝑎 𝐼 𝑑𝑑 - Joule (resistive) heating power Units: 1J/1s =1Watt (W) 3 Problem What is the maximum power one can get (dissipate in the load) from a given (ℰ, 𝑟) battery? 𝑉 ℰ =𝐼 𝑟+𝑅 𝑃= 𝑃 “current” source r>>R 𝑑𝑑 1 ∝ 𝑑𝑑 𝑟+𝑅 −2 2 𝑟 + 𝑅 − 2𝑅 = 0 𝑅 𝑟+𝑅 𝑅𝐼2 ∝𝑅 3 𝑅=𝑟 =0 𝑅 = 𝑟+𝑅 𝑟 2 ℰ 2 “voltage” source r<<R ∝ 1/𝑅 𝑅 𝑃𝑚𝑚𝑚 → @ 𝑅 = 𝑟 6 Light Bulbs The incandescent light bulb: a resistor, being heated by current, emits black-body radiation in the visible wavelength range. Bulbs are rated by power. Resistance of a 60W bulb designed for 120V (neglect the fact that this rating is for the AC (not DC) current): 𝑉2 120𝑉 2 𝑅= = = 240Ω 𝑃 60𝑊 Note that a light bulb that is rated at 60W actually produces only about 3 W of visible light The larger the power, the smaller the resistance (we assume that R is much greater than the internal resistance of the voltage source). 𝑃 The wall outlet 110V can be considered as a voltage source – the internal resistance is smaller than all typical loads. ∝𝑅 𝑟 ∝ 1/𝑅 𝑅 (𝑟 is fixed) 7 Kirchhoff’s Junction Rule Junction Rule (for currents): charge conservation � 𝐼𝑖 = 0 𝑖 Currents flowing in → + Currents flowing out → - 14 Kirchhoff’s Loop Rule 𝑟 𝑉 ℰ 𝑅 ℰ Loop Rule (energy conservation): � ℰ𝑖 + � 𝑉𝑖 = 0 𝑖 𝑖 for any closed loop � 𝑉𝑖 = 0 𝑖 𝐼𝐼 𝐼𝐼 𝑥 if we neglect the difference between 𝑉’s and ℰ’s, and accept the sign conventions. 15 Example We don’t need to know a priori the actual direction of the current: if we get the negative value of I, that would mean that the current flows in the direction opposite to the direction of “travel”. � ℰ𝑖 + � 𝑉𝑖 = 0 𝑖 𝑖 −4𝑉 + 12𝑉 − 𝐼 7Ω + 2Ω + 3Ω + 4Ω = 0 8𝑉 𝐼= = 0.5𝐴 16Ω 16 Example (cont’d) V 4Ω “4V” 7Ω “12V” 2Ω 3Ω a – reference voltage =0 17 More Examples 6Ω 3Ω (a) 3Ω 3Ω 6Ω 36𝑉 𝐼= = 4𝐴 9Ω Problem 26.77: (a) what is the potential difference Vab when the switch is open? (b) What is the current through the switch when the switch is closed? (c) What is the equivalent resistance when the switch is closed? 𝑉𝑎 = 36𝑉 − 6Ω ∙ 4𝐴 = 12𝑉 𝑉𝑏 = 36𝑉 − 3Ω ∙ 4𝐴 = 24𝑉 𝑉𝑎 − 𝑉𝑏 = 12𝑉 − 24𝑉 = −12𝑉 20 More Examples (cont’d) 6Ω 3Ω 3Ω 3Ω ℰ 6Ω 1 Problem 26.77: (b) What is the current through the switch when the switch is closed? (b) loop 1: 36 − 6 ∙ 𝐼1 − 3 ∙ 𝐼1 − 𝐼3 = 0 loop 2: −6 ∙ 𝐼1 − 3 ∙ 𝐼3 + 3 ∙ 𝐼2 = 0 2 3 𝐼1 = 36 10.5 Choose (arbitrary) directions of currents and travel along the loops. Note that the “current” rule has been taken care of. loop 3: −3 ∙ 𝐼1 − 𝐼3 + 6 ∙ 𝐼2 + 𝐼3 + 3 ∙ 𝐼3 = 0 + 𝐼3 = 𝐼2 − 2𝐼1 (from Eq.2) −3 ∙ 𝐼1 + 12 ∙ 𝐼3 + 6 ∙ 𝐼2 = 0 (from Eq.3) −3 ∙ 𝐼1 + 12 ∙ 𝐼2 − 24 ∙ 𝐼1 + 6 ∙ 𝐼2 = 0 3 𝐼2 = 𝐼1 2 36 − 6 ∙ 𝐼1 − 3 ∙ 𝐼1 + 3 𝐼2 − 2𝐼1 = 36 − 10.5 ∙ 𝐼1 = 0 3 𝐼3 = 𝐼1 − 2𝐼1 = −0.5𝐼1 2 𝐼3 = − 18 = −1.71 10.5 “-” means that our initial direction of I3 has to be reversed. 21 More Examples (cont’d) 6Ω 3Ω 3Ω 3Ω 6Ω Problem 26.77: (a) what is the potential difference Vab when the switch is open? (b) What is the current through the switch when the switch is closed? (c) What is the equivalent resistance when the switch is closed? (c) ℰ 1 2 3 𝑰 + 𝐼1 = 𝑅𝑒𝑒 ℰ = 𝐼 𝐼 = 𝐼1 + 𝐼2 36 10.5 3 𝐼2 = 𝐼1 2 𝑅𝑒𝑒 = 𝐼 ≈ 8.6𝐴 36𝑉 = 4.2Ω 8.6𝐴 22 Conclusion Resistors in Series and Parallel Voltmeters and Ammeters Kirchhoff’s Rules Next time: Lecture 12: RC circuits §§ 26.4 23 Voltmeters The goal: to measure the voltage difference across an element (ideally, without affecting the circuit due to the voltmeter connection). V 𝑹𝒊𝒊 An ideal voltmeter: A. has 𝑹𝒊𝒊 = 𝟎 and should be connected in parallel with the circuit element being measured. 𝑹 V 𝑹 𝑹𝒊𝒊 B. has 𝑹𝒊𝒊 = 𝟎 and should be connected in series with the circuit element being measured. C. has 𝑹𝒊𝒊 = ∞ and should be connected in parallel with the circuit element being measured. D. has 𝑹𝒊𝒊 = ∞ and should be connected in series with the circuit element being measured. 24 Voltmeters The goal: to measure the voltage difference across an element (ideally, without affecting the circuit due to the voltmeter connection). V 𝑹𝒊𝒊 An ideal voltmeter: A. has 𝑹𝒊𝒊 = 𝟎 and should be connected in parallel with the circuit element being measured. 𝑹 V 𝑹 𝑹𝒊𝒊 B. has 𝑹𝒊𝒊 = 𝟎 and should be connected in series with the circuit element being measured. C. has 𝑹𝒊𝒊 = ∞ and should be connected in parallel with the circuit element being measured. D. has 𝑹𝒊𝒊 = ∞ and should be connected in series with the circuit element being measured. Voltmeter: high internal resistance 25 Ammeters The goal: to measure the current in a circuit element (ideally, without affecting the current due to the ammeter connection). I 𝑹𝒊𝒊 An ideal ammeter: A. has 𝑹𝒊𝒊 = 𝟎 and should be connected in parallel with the circuit element being measured. 𝑹 I 𝑹 𝑹𝒊𝒊 B. has 𝑹𝒊𝒊 = 𝟎 and should be connected in series with the circuit element being measured. C. has 𝑹𝒊𝒊 = ∞ and should be connected in parallel with the circuit element being measured. D. has 𝑹𝒊𝒊 = ∞ and should be connected in series with the circuit element being measured. 26 Ammeters The goal: to measure the current in a circuit element (ideally, without affecting the current due to the ammeter connection). I 𝑹𝒊𝒊 An ideal ammeter: A. has 𝑹𝒊𝒊 = 𝟎 and should be connected in parallel with the circuit element being measured. 𝑹 I 𝑹 𝑹𝒊𝒊 B. has 𝑹𝒊𝒊 = 𝟎 and should be connected in series with the circuit element being measured. C. has 𝑹𝒊𝒊 = ∞ and should be connected in parallel with the circuit element being measured. D. has 𝑹𝒊𝒊 = ∞ and should be connected in series with the circuit element being measured. Ammeter: low internal resistance 27 Appendix 1: Built-in Battery Tester Bi-layer structure: the thermochromic (non-conductive) ink deposited on top of the conductive ink. 𝑅𝑒𝑒 𝑉 𝑟 1 1 1 = + + 𝑅1 𝑅2 𝑅3 𝐼= ℰ 𝑟 + 𝑅𝑒𝑒 𝑉𝑎𝑎 2 𝑃1 = 𝑅1 −1 𝑉𝑎𝑎 = 𝑅1 𝑅2 𝑅3 𝑅1 𝑅2 + 𝑅1 𝑅3 + 𝑅2 𝑅3 𝑅𝑒𝑒 = ℰ − 𝐼𝐼 = ℰ 𝑟 + 𝑅𝑒𝑒 𝑉𝑎𝑎 2 𝑃2 = 𝑅2 𝑉𝑎𝑎 2 𝑃3 = 𝑅3 ∆T of the thermochromic ink is proportional to P/area: (e.g., 𝑃3 is ~2 times smaller than 𝑃1 , and its area is 2 times greater) 𝑃1 𝑃2 𝑃3 : : = 4: 2: 1 𝐴1 𝐴2 𝐴3 28 𝐼1 𝐼2 V 12Ω ℰ > 63V = 75V − 12Ω ∙ 1𝐴 15Ω