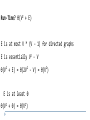Download 141209_Review_Slides_2

CS104 Final Exam
Review
Fall 2014
Johnathan Mell & Alana Shine
Adapted from Johnny Jung / Peter Zhang
Cover Major Topics: See Piazza for full list
 Basic C++ concepts
 Data structures
 Algorithms
 Running time analysis
 Object-oriented concepts
 C++ syntax
 Event-oriented programming (Qt)
 Randomness
Questions Any Time
Basic C++
Dynamic Memory


Why do we care about dynamic memory?
Why can’t we just allocate everything statically?



int stuff[]
Ok, so if we need dynamic allocation, why do we care
about delete?
Who should delete things?
Examples
void myFunc()//worst
{
int * stuff = new int[4];
}
int * myFunc()//bad
{
return new int[4];
}
Passing data back and forth
By value:
Thing func(int a)
{
a = 4;
Thing b(a);
return b;
}
By reference:
Thing & func(int &a)
{
*a = 4;
Thing b(*a);
return &b;
}
By pointer:
Thing * func(int * a)
{
*a = 4;
Thing * b = new
Thing (*a);
return &b;
}
Review:





*a //the value stored at a
a* //a pointer to an a
a //an a
a& //an address of an a (very similar to a*)
&a //the address of an a
Ugh. What should I use?!



Use values most often. Will create a local copy. Slight
overhead, most compilers optimize.
Use pointers occasionally. Hardly ever should you use
new if you do not also call delete.
(not covered): For real C++, use smart pointers, which
are the new way of dealing with this. (Also, stop saying
“using namespace std;”)
Data Structures and their Analysis
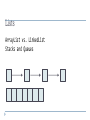
Lists
ArrayList vs. LinkedList
Stacks and Queues
class LinkedList {
protected:
Node* head;
}
class Queue : public LinkedList {
public:
int pop();
void push(int);
};
void Queue::push(int newValue) {
Node* tail = head;
while(tail->next != NULL) {
tail = tail->next;
}
Node* newNode = new Node;
newNode->value = newValue;
tail->next = newNode;
}
int Queue::pop() {
int toReturn = head->value;
head = head->next;
delete head-> prev;
return toReturn;
}
Q: Implement Queue with an ArrayList
class ArrayList {
protected:
int capacity;
int* array;
}
Q: Implement Queue with an ArrayList
Solution 1:
Shift everything every pop.
2 5 4 6 8 _ _ _
_ 5 4 6 8 _ _ _
5 4 6 8 _ _ _ _
Runtime: O(n)
Solution 2:
class Queue : public ArrayList {
private:
int headIndex;
int tailIndex;
};
int inc(index) {
if(index + 1 == capacity) {
return 0;
} else {
return index + 1;
}
}
void Queue::push(int newValue) {
if(inc(tailIndex) == headIndex) {
expand();
}
tailIndex = inc(tailIndex);
array[tailIndex] = newValue;
}
int Queue::pop() {
if(headIndex == tailIndex) {
throw out_of_range(“list is empty”);
}
headIndex = inc(headIndex);
return array[headIndex];
}
Sets

Sets are like lists but they are :


Lacking an ordering
Free of duplicates
Sorts
Q: What sort would you use to sort 1 million
items?
Q: What sort would you use to sort 20 items?
Examples! - Best, Worst, Average Case
Bubble Sort - Ɵ(n2)
Selection Sort - Ɵ(n2)
Insertion Sort - Ɵ(n2) (Best Case - Ɵ(n))
Merge Sort - Ɵ(n log n)
Quick Sort - Ɵ(n log n) (Worst Case - Ɵ(n2))
Heap Sort - covered later - Ɵ(n log n)
Trees
A complete, acyclic graph.
Useful in: sorting, modeling parent/children
relationships
•
Binary Tree:
•
•
Binary Search Tree:
•
•
•
Each node has at most 2 children
Binary tree with each node:
Left child < current node < right child
Heap (min or max):
•
•
Children < or > parents
Not a binary search tree!
Lookup in a BST:
We visit each level only once.
There are only log2 n levels.
O(log2 n)
Sort with a BST:
- Insert all elements from array into BST
- Traverse
Sort with a BST:
- Insert all elements from array into BST
> insert one element = O(log n)
> n elements in total
> total: average O(n log n)
- Traverse = O(n)
Sort with a BST:
+ Insert all elements from array into BST
> insert one element = O(lg n)
> worst case O(n)
> n elements in total
> total: average O(n lg n)
worst
O(n2)
+ Traverse
O(n)
= O(n lg n) -> O(n2)
Q: How do you know if a tree is balanced?
Q: How do you know if a tree is balanced?
A tree is balanced if the max depth of the
tree is less than 1 away from the min depth.
Q: How do you know if a tree is balanced?
How do you calculate depth?
- leaf has depth of 0
- parent of a leaf has depth of 1
- grandparent of leaf has depth of 2
Q: How do you know if a tree is balanced?
How do you calculate depth?
int depth(Node node) {
if(node == NULL) { return 0; }
return 1 + depth(node.child);
}
Q: How do you know if a tree is balanced?
int maxDepth(Node node) {
if(node == NULL) { return 0; }
return 1 + Math.max(maxDepth(node.left),
maxDepth(node.right));
}
Q: How do you know if a tree is balanced?
bool isBalanced(Node head) {
return maxDepth(head) - minDepth(head) <=
1;
}
runtime: O(n) - why?
Q: Given two nodes, p and q, in one tree, find
the common ancestor
Q: Given two nodes, p and q, in one tree, find
the common ancestor
The common ancestor has node p in one subtree
and q in the other subtree.
How do you know if a node belongs to a subtree?
Q: Given two nodes, p and q, in one tree, find
the common ancestor
bool contains(Node head, Node target) {
if(head == null) { return false; }
if(head == target) { return true; }
if(head != target) {
return contains(head.left, target) ||
contains(head.right, target));
}
}
Q: Given two nodes, p and q, in one tree, find
the common ancestor
Node commonAncestor(Node head, Node p, Node q) {
if(contains(head.left, p) && contains(head.left, q) {
return commonAncestor(head.left, p, q);
} else if(contains(head.right, p) && contains(head.right,
q) {
return commonAncestor(head.right, p, q);
} else {
return head;
}
}
Keeping a tree balanced is very important.
2-3 Tree
Red Black Tree
2-3 Tree
A node can have 1 or 2 values, with 2 or 3
children.
2-3 Tree Insertion
- Insert at normal BST node
- If node was a 2-node, you’re done.
- If node was a 3-node, promote median value up
2-3 Tree Removal
- If target is not leaf node, swap with the inorder successor
- remove target
- if node is now empty, fixTree on target
- if sibling has two elements, redistribute
- else, merge sibling and parent into one
node, call fixTree on parent
Red Black Tree
- Binary Search Tree
- Nodes are assigned red / black color
- Any path down to a leaf cannot have two
consecutive red nodes.
Red Black Tree insertion
- insert, mark node as red
- if parent is black = ok
- else fixTree
Red Black Tree fixTree
if uncle is red
recolor
fixTree(grandParent)
else
if(zigzag) { rotate to straight line }
rotate other direction
Heap:
Each node always has the same relationship
with its children
MaxHeap:
Each node is bigger than its children
You can inplace traverse a BST, but not a
Min/MaxHeap!
Sort with Heap:
Elements will not chain up, therefore will not
have the worst case scenario in BST.
O(n log n)
Priority Queue
With a Heap, we can only get the top item or
insert an item at the back. Sounds familiar?
We can also use heaps to organize objects for
us, not just primitive types.
If we give objects a “queue order” value, we
can insert them in a heap and get them back in
an order.
Student johnathan;
Student alana;
Student kempe;
PriorityQueue<int, Student> pq;
pq.insert(50, johnathan);
pq.insert(25, alana);
pq.insert(100, kempe);
cout << pq.top(); //kempe
Tries
Implement a map where the key is a string
Use a tree to store this…
If we use binary search tree…
Search = Ɵ(log n)
String comparison = Ɵ(m) where m is length of
string
Can we do better?
Use a trie! Ɵ(m)
Each node stores a prefix of the key
- mark which nodes are terminating
- start at root and and move downwards until
you reach terminating or can’t find it
ex) HEAP, HEAL, HEAR, HEART
Algorithms
Searches and Sorting


We’ve covered binary.
What about interpolation?



What assumptions are made?
How do you break it?
See above for Sorting discussion
Traversals
Pre-Order
In-Order
Post-Order
Visiting each node in a systematic way...
void pre_order(Node * n) {
if(n == NULL) return;
cout << n->value;
pre_order(n->left);
pre_order(n->right);
}
Hint: just move left to right!
Example on board.
void in_order(Node * n) {
if(n == NULL) return;
in_order(n->left);
cout << n->value;
in_order(n->right);
}
void post_order(Node * n) {
if(n == NULL) return;
post_order(n->left);
post_order(n->right);
cout << n->value;
}
Q: Print all nodes of a BST in reverse order
(greatest to least).
void BST::reverse_print();
struct Node {
Node *left, *right, *parent;
int value;
};
class BST {
void insert(int value);
bool contains(int value);
void print();
Node *root;
}
Solution
void BST::reverse_print() {
reverse_print_helper(root);
}
void BST::reverse_print_helper(Node * n) {
reverse_print_helper(n->right);
cout << n->value;
reverse_print_helper(n->left);
}
Run-Time?
We visit every node in the graph once.
cout << n->value << endl; is a constant-time
operation
Run-Time?
We visit every node in the graph once.
cout << n->value << endl; is a constant-time
operation
Ɵ(n)
Run-Time?
What if we did process(n) instead of cout << n>value << endl;
process(n) is a Ɵ(d) operation where d is not a
constant
Run-Time?
What if we did process(n) instead of cout << n>value << endl;
process(n) is a Ɵ(d) operation where d is not a
constant
Ɵ(nd)
Graphs
Adjacency List O(V+E)
- List for each vertex
Adjacency Matrix O(V2)
- VxV matrix for each edge
Directed Graphs?
Q: Convert a graph in adjacency list format to
adjacency matrix format.
Q: Convert a graph in adjacency list format to
adjacency matrix format.
Psuedo-Code
- Create adjacency matrix based on size of
adjacency list
- Pre-fill with zeroes for every value
- Go through each adjacency list and add ones
to matrix where needed
Run-Time?
Have to create adjacency matrix and pre-fill it
with zeroes. How many elements in matrix?
Have to look at all the nodes in the adjacency
lists. How many elements in adjacency lists?
Ɵ(V2 + E)
Run-Time? Ɵ(V2 + E)
E is at most V * (V - 1) for directed graphs
E is essentially V2 - V
Ɵ(V2 + E) = Ɵ(2V2 - V) = Ɵ(V2)
E is at least 0
Ɵ(V2 + 0) = Ɵ(V2)
Graph Algorithms
DFS
BFS
Dijkstra’s
DFS: Go as far as possible and then backtrack
BFS: Visit all of node’s neighbors first
Dijkstra’s: Similar to BFS, greedy approach to
picking what node to go to next. Does not
work with negative edge weights. Does not
work with cycles. See A* for the negative
edge weight problem. Cycles are more
problematic…
Q: Implement DFS
Solution
void DFS(Vertex v) {
v.visited = true;
cout << v.value << endl;
for all Vertex w where v->w exists {
if(!w.visited) {
DFS(w);
}
Q: Implement a DFS iteratively. (Palantir SE
interview question)
Let’s use a stack!
Solution
void DFS_iterative(Vertex v) {
Stack s;
s.push(v);
while(!s.empty()) {
v = s.peek(); s.pop();
if(!v.visited) {
v.visited = true;
cout << v.value << endl;
for all Vertex w where v->w exists {
s.push(w);
}
}
}
}
Dijkstra
Uses a priority queue
(how did we implement priority queues?)
(heaps!)
Examples!
BFS
DFS
Dijkstra
More interview questions...
Q1: Find if a given undirected graph has a
cycle.
Q2: Find the closest distance to a friend in a
social network.
Hashing
Ɵ(1) operations
You should have a good reason if you’re not
using hashing
hash function
h(k) -> integer
hash function
- convert data type to an integer
- use modulo to keep it within table
Collisions! What are they?
How to avoid?
Key take away: Hashing is often very fast, but
can have worst case running time that is
problematic if you have many collisions.
Follow-up to sets (Bloom Filters)





We can use hashes to move quickly through sets using a
“Bloom Filter”
A Bloom Filter is an approximation. It is subject to false
positives.
Basically, we use a series of hashes to set bits in an array when
adding.
If, when we look up an element, the any bit is set to 0 when
fed through the same hash, the element cannot be in the set.
But, it may or may not be there when they are all 1. Why?
This is a data structures course...
- Know ALL of them, operations, run-time
- Advantages, disadvantages
- Implementations for them
Priority Queues, Heaps, Maps, Hash, BST, RedBlack Trees, Bloom Filters, Tries, etc.
Object-Oriented Programming
Everything is an object




Some are primitives (int, char)
Most are not (String, Foo)
Objects must be declared somewhere.
They are either structs or classes.


Objects have members, accessible through dot notation.


What’s the difference?
Foo.member
Pointers are objects too (but they are primitive).


What are they? (ints).
This is why NULL works. (but you should use nullptr).
Objects may inherit from other objects


Why?
Because we want to reuse code (private inheritance)


Because we want to make certain assumptions about the
functions present (public inheritance).


This is called (rarely) AS-A relationships
This is called IS-A relationships
Note that HAS-A relationships have nothing to do with
inheritance! NOTHING.
Inheritance leads to polymorphism
A class inherits from another.
 It may then later be treated as its parent or itself due to
the circumstances. This is polymorphism.
 Say Car inherits from Vehicle.
Car bar;
Vehicle foo;

Polymorphism example
Now we have a function Pilot in Vehicle, and a function
TurnSignal in Car.
bar.TurnSignal //ok!
foo.TurnSignal //not ok!
 Now let’s declare the Pilot function virtual!
bar.Pilot() //calls the Car’s function
foo.Pilot() //calls the Vehicle’s function

Polymorphism continued
But now suppose we said:
Vehicle * extra = &foo; //legal
extra->Pilot()//calls Vehicle’s function!!!
 We can avoid this problem by making Vehicle “abstract”,
thus forcing us to avoid instantiating Vehicles and allowing
Cars to be treated correctly.
 Now extra->Pilot() works!

C++ Advanced Syntax
Templates


Why?
Because we cannot anticipate ahead of compile time
which objects may be required!

A list of Birds? Of ints?
Exceptions





Why?
Better than returning an integer code you have to cross reference
against a printed manual. Yuck.
Why not?
Leaves program in unknown state.
Should only be used when something truly EXCEPTIONAL happens.
Most people agree this is when the programs fails due to “outside
factors”.



Server crashes
Operating system is out of room
It is a grey area. You can always opt never to use them. (See Google)
Operators!





+*-/<<>>==!=
All can be overloaded!
This means you can write a custom print for <<
Or make meaningful vector arithmetic with + or *.
Iterators require it.
Speaking of…



Iterators are used to traverse some data structure in a
meaningful way.
In a tree, you could opt for in-order or pre-order
traversal, for example.
Iterators are needed for things that have no easily
understood ordering (like sets or trees). They are not
generally as necessary for lists.
Constructors and Destructors










All objects call their default constructor when declared like this:
Foo a;
Foo * a = new Foo();
Foo a();
The second iteration needs to be deleted manually.
Upon manual or automatic (when does this happen?) deletion, a destructor
is called.
A copy constructor is a special constructor that is called here:
Foo b = a;
It is NOT called here (why)?:
Foo a, b;
b = a; //assignment operator
Why use const?
Const is a guarantee that data has not been manipulated.
 It is normally good style not to modify incoming objects, but
this is not enforced without const.
int foo (int * a)
{ return *a + 1;}
int foo (int * a)
{ *a += 1; return *a;}

The first function can be declared const. The second cannot.

Public and Private
In classes, fields are considered private unless otherwise specified.
This prevents outsiders from manipulating important internals!
 Example:
Class BankAccount{
Public:
int myPin;
void login(int pin);
}
 Problem! Why?
 You may add “getters” and “setters” to access private variables if
need be.

Event-oriented programming (Qt)
Linear program flow and why it fails us


GUIs inherently involve many options that could happen
at any given time
We could make a giant while loop and see what is
pressed.



This is now a “busy wait”
It is very cumbersome
We prefer to just mark certain actions as events and deal
with them whenever!
Events

Pros:



No busy wait
Much simpler code
Cons:


Can happen at ANY time
Must be self-contained because of this
Qt and events




In Qt, we implement this as signals and slots
Signals are any of several things that can happen, like
button pushes, or closing a window, or typing
Slots are the functions that are called when those happen.
Again, we don’t know when these functions may be
called!
Qt widgets



Qt uses objects called widgets, which have a number of
handy built-in properties.
They can be easily displayed on the screen using layouts.
They can inherit from each other quite easily.
Interview Problems
Q: For a music service, users may like
different artists. Which artist do the users
like the most?
(Startup screening question)
Q: Given a list of unsorted integers, return
the lowest positive number not in the list.
(_oogle SWE Interview Question)
Randomness
Some representative problems
Q: Construct a tree given all the parent-child
relations. (_oogle SWE Interview Question)
Q: n Queens problem (Facebook SE Interview
Question)
Q: Parse XML and construct a tree from it
(Microsoft SDE Interview Question)
Q: kth-order statistic (Find the kth largest
value of a list in Ɵ(n) time) (Microsoft SDE
Interview Question
Q: Implement Dijkstra’s (Can’t get much
straight forward than this lol) (Palantir SE
Interview Question)
Q: Given a file input, correctly implement an
iterator that returns one word at a time
(_oogle SWE Interview Question).
Good Luck!