Download Material since exam 3

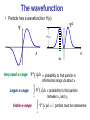
Material since exam 3
• De Broglie wavelength, wavefunctions, probabilities
• Uncertainty principle
• Particle in a box
– Wavefunctions, energy, uncertainty relation
– 1D, 2D, and 3D box, wavefunctions, energy
• 3D hydrogen atom
– Quantum #’s, physical meaning of quantum #’s
– Energies and wavefunctions
– Orbital magnetic dipole moment, electron spin
• Multielectron atoms
– State energies, electron configuration, periodic table
– Lasers
• Nuclear physics
– Isotopes, nuclear binding energy
– Radioactive decay
• Decay rates, activity, radiation damage
• Types of decay, half-life, radioactive dating.
Matter waves
• If light waves have particle-like properties,
maybe matter has wave properties?
• de Broglie postulated that the
wavelength of matter
is related to momentum as
h

p
• This is called
the de Broglie wavelength.
Nobel prize, 1929
Matter Waves
• deBroglie postulated that matter has wavelike
properties.
• deBroglie wavelength   h / p
Example:
Wavelength of electron with 10 eV of energy:

Kinetic energy
p2
E KE 
 p  2mE KE
2m
h
hc
1240eV  nm



 0.39nm
2
6
2mE KE
2mc E KE
20.51110 eV 10eV 
Heisenberg Uncertainty
Principle
• Using
– x = position uncertainty
– p = momentum uncertainty
• Heisenberg showed that the product
( x )  ( p ) is always greater than ( h / 4 )
Often write this as
  
x p
~
is pronounced
‘h-bar’
where
h

2

/2
Planck’s
constant
The wavefunction
• Particle has a wavefunction (x)
2
0.2

0.15
2(x)
0.1
0.05
0
x
-0.05
-4
-3
-2
-1
0
1
2
dx
Very small x-range
x
3
4
2 xdx = probability to find particle in
infinitesimal range dx about x
x2
Larger x-range

Entire x-range
  xdx = probability to find particle
2
x1



between x1 and x2
 2 x dx  1 particle must be somewhere
Question
2
0.5nm-1
0.2
0.15
0.1
What is probability that particle is found
in 0.01nm wide region about -0.2nm?
0.05
0
A.
0.001
B.
0.005
C.
0.01
D.
0.05
E.
0.1
-0.05
-4
About what is probability that particle is
in the region -1.0nm<x<0.0nm?
A.
0.1
B.
0.4
C.
0.5
D.
1.5
E.
3.0
-0.8nm
-3
-2
-0.2nm
-1
0
0
1
2
x
3
Particle in 1D box
h

p2
E
2m
h
2L /3
2
h
32
8mL2
 n=2
h

2L /2
h2
2
8mL2
 n=1
 h
2L
h2
8mL2
n
n=3

p

2
L
Wavefunction
Probability
• Quantized momentum
h
h
p 
 npo
 2L /n
• Energy = kinetic
2
2
npo 
p

E

 n2Eo

2m
2m

• Or Quantized Energy
Energy
Particle in box energy levels
n=5
n=4
En  n2Eo
n=3
n=quantum number
n=2
n=1
3-D particle in box: summary
• Three quantum numbers (nx,ny,nz) label each state
– nx,y,z=1, 2, 3 … (integers starting at 1)
• Each state has different motion in x, y, z
• Quantum numbers determine px 
– Momentum in each direction: e.g.
h
n
 nx
x
h
2L
2
2
p
p
p
– Energy: E 
 y  z  E o nx2  ny2  nz2 
2m 2m 2m
2
x
• Some quantum states have same energy

Question
How many 3-D particle in box spatial quantum
states have energy E=18Eo?
A. 1
B. 2
C. 3
D. 5
E. 6
E  E o n x2  n y2  n z2 
n ,n ,n  4,1,1, 1,4,1, (1,1,4)
x

y
z
Q: ask what state is this?
(121)
(211)
All these states have the same
energy, but different probabilities
(112)
3D hydrogen atom
mS
Spin magnetic quantum
number
+1/2 or -1/2
2
For hydrogen atom:
•
•
•
•
n describes energy of orbit : E  13.6 /n 2 eV
ℓ describes the magnitude of orbital angular momentum
m ℓ describes the angle of the orbital angular momentum
 of the spin angular moment
ms describes the angle
 n  2 



0


 m  0 

1 
ms   

2 

Other elements: Li has 3
electrons
 n  2 



0


 m  0 

1 
ms   

2 
 n  2 



1


 m  0 

1 
ms   

2 
 n  2 



1


 m  0 

1 
ms   

2 
 n  2 



1


 m  1 

1 
ms   

2 




 n  2 



1


 m  1 

1 
ms   

2 
 n  1 


  0 
 m  0 


m s  1/2
 n  2 



1


m  1 

1 
ms   

2 
n=2 states, 
8 total, 1 occupied
n=1 states,
2 total, 2 occupied
 n  1 


  0 
 m  0 


m s  1/2
 n  2 



1


m  1 

1 
ms   

2 
one spin up, one spin down
Question
Inert gas atoms are ones that have just enough electrons to finish filling
a p-shell (except for He). How many electrons do next two inert gas
atoms after helium ( neon (Ne) and argon (Ar) ) have.
In this range of atomic number the subshells fill in order of increasing
angular momentum.
A. 10 & 18
B. 4 & 8
C. 8 & 16
D. 12 & 20
E. 6 & 10
Multi-electron atoms
• Electrons interact with
nucleus (like hydrogen)
• Also with other electrons
• Causes energy to
depend on ℓ
States fill in order of energy:
1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d
Energy depends
on n and
ℓ
Energy
depends only
on n
The periodic table
• Atoms in same column
have ‘similar’ chemical properties.
• Quantum mechanical explanation:
similar ‘outer’ electron configurations.
H
1s1
Li
2s1
Na
3s1
K
4s1
Be
2s2
Mg
3s2
Ca
4s2
Sc
3d1
Y
3d2
8 more
transition
metals
B
2p1
Al
3p1
Ga
4p1
C
2p2
Si
3p2
Ge
4p2
N
2p3
P
3p3
As
4p3
O
2p4
S
3p4
Se
4p4
F
2p5
Cl
3p5
Br
4p5
He
1s2
Ne
2p6
Ar
3p6
Kr
4p6
Electron Configurations
Atom
Configuration
H
1s1
He
1s2
Li
1s22s1
Be
1s22s2
B
1s22s22p1
Ne
etc
1s shell filled
1s22s22p6
(n=1 shell filled noble gas)
2s shell filled
2p shell filled
(n=2 shell filled noble gas)
Ruby laser operation
Relaxation to
metastable state
(no photon
emission)
3
e
V
2
Metastable
state
e
V
PUMP
1
e
V
Transition by
stimulated emission of
photon
Ground state
Isotopes
# protons
• Carbon has
6 protons, 6 electrons (Z=6):
this is what makes it carbon.
Total # nucleons
12
C
6
• Most common form of carbon has 6 neutrons
in the nucleus. Called 12C
Another form of carbon has
6 protons, 8 neutrons in the nucleus. This is 14C.
This is a different ‘isotope’ of carbon
Isotopes: same # protons, different # neutrons
Nuclear matter


Any particle in nucleus, neutron or proton, is
called a nucleon.
“A” is atomic mass number


A=total number of nucleons in nucleus.
Experimental result

All nuclei have ~ same (incredibly high!) density of
2.3x1017kg/m3
Volume A = number of nucleons
Radius  A1/3

r  ro A1/ 3,


ro  1.2 fm  1.2 1015 m
Binding energy
• Calculate binding energy from masses
E binding  Zmp  NmN  mnucleusc 2
Zme
Zme
E binding  ZmH  NmN  matom c 2


Mass of
Hydrogen atom
(1.0078 u)
Mass of atom with
Z protons, N neutrons

Atomic masses well-known-> easier to use
Biological effects of radiation
• Radiation damage depends on
– Energy deposited / tissue mass (1 Gy (gray) = 1J/kg)
– Damaging effect of particle (RBE, relative biological effectiveness)
Radiation type
RBE
X-rays
Gamma rays
Beta particles
Alpha particles
1
1
1-2
10-20
• Dose equivalent = (Energy deposited / tissue mass) x RBE
– Units of Sv (sieverts) [older unit = rem, 1 rem=0.01 Sv]
– Common units mSv (10-3Sv), mrem (10-3rem)
– Common ‘safe’ limit = 500 mrem/yr
(5 mSv/yr)
Exposure from 60Co source
Co source has an activity of 1 µCurie 3.7 10 decays /s
• 60
• Each decay: 1.3 MeV photon emitted
• Hold in your fist for one hour
4
– all particles absorbed by a 1 kg section of your body for 1 hour
• Energy absorbed in 1 kg =
1.310 eV 1.6 10
6
19

J /eV 3.7 104 decays /s1hr3600s/hr  2.8 105 J
What dose do you receive? A. 0.5 rem
5
2.8
10
J /kg1rad /0.01J /kg

B. 0.3 rem
C. 0.1 rem
D. 0.05 rem
 0.003 rad = 0.003 rem
E. 0.003 rem
Quantifying radioactivity

Decay rate r



Prob( nucleus decays in time t ) = r t
(Units of becquerel (1 Bq=1 s-1) or
curie (1 Ci=3.7x1010 s-1)
Activity R

Mean # decays / s = rN,
Half-life t1/2

(Units of s-1)
N=# nuclei in sample
(Units of s)
time for half of nuclei to decay = t1/2
N  N oer t
ln 2 0.693


r
r
Activity of Radon
• 222Rn has a half-life of 3.83 days.
• Suppose your basement has 4.0 x 108
such nuclei in the air. What is the activity?
We are trying to find number of decays/sec.
So we have to know decay constant to get R=rN
0.693
0.693
r

 2.09 106 s
t1/ 2
3.83days  86,400s /day
dN
R
 rN  2.09 106 s  4.0 10 8 nuclei  836decays /s
dt
1Ci
R  836 decays /s 
 0.023Ci
10
2.7 10 decays /s
Decay summary
• Alpha decay
– Nucleus emits He nucleus (2 protons, 2 neutrons)
– Nucleus loses 2 protons, 2 neutrons
• Beta- decay
– Nucleus emits electron
– Neutron changes to proton in nucleus
• Beta+ decay
– Nucleus emits positron
– Proton changes to neutron in nucleus
• Gamma decay
– Nucleus emits photon
as it drops from excited state