Download Complex numbers Summary PPTX

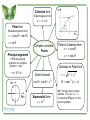
Complex numbers
•Definitions
•Conversions
•Arithmetic
•Hyperbolic Functions
Define the imaginary number
i  1
so that
i 2  1,
If z  x  iy
then x is the real part of z
and y is the imaginary part
i 3  i  i 2  i
i 4  i 2i 2  1  1  1
Im z
Argand diagram
x  iy
y
r

x
Main page
Re z
Complex numbers:
Definitions
If z  x  iy then
the conjugate of z ,
written z or z *
is x  iy
If the complex number z  x  iy then
the Modulus of z is written as z and
the Argument of z is written as Arg (z )
so that
z  x 2  y 2  r , Arg ( z )  tan 1 ( y / x)  
r ,  are shown in the Argand diagram
Cartesian form
(Real/Imaginary form)
z  x  iy
Polar form
Complex numbers:
Forms
If  is the principal
argument of a complex
number z then
Re z
Main page
Re z
Polar to Cartesian form
x  r cos 
y  r sin 
Cartesian to Polar form
Eulers formula
cos   i sin   ei
Im z
r
x
Principal argument
    
x  iy
y

(Modulus/Argument form)
z  r (cos   i sin  )
 r cis 
Im z
Exponential form
z  re i
r
x2  y2
  tan 1 ( y / x)
NB. You may need to add or
1
subtract
to tan ( y / x)
in order that  gives z in the
correct quadrant

Let z  a  ib
and w  c  id
Multiplication
z  w  (a  ib )(c  id )
 (ac  bd )  i (ad  bc)
Addition/ subtraction
z  w  (a  c)  i (b  d )
Equivalence
Complex numbers:
Arithmetic
z  w  a  c and b  d
De Moivres theorem
Division
(cos   i sin  ) n  cos n  i sin n
z z  w z  w (a  ib )(c  id )



w w w w 2
c2  d 2
Polar/ exponential form:
Powers/ roots
 ac  bd   bc  ad 
 2
 i 2
2 
2 
c d  c d 
If z
then
 r n ei ( n )
Polar/ exponential form: Mult/division
If z 
then
r cis   re i
and
w  s cis   se i
z  w  rs cis(    )  rse
and z
r
r
   cis(    )   e i(  )
w s
s
 r cis   re i
z n  r n cis (n )
and
 n
n
z  n r cis 

n
i(  )
re
 n
i
Main page
Hyperbolic Sine & Cosine Functions
cosh x 



1 x
1 x
e  e  x and sinh x 
e  e x
2
2
Other Hyperbolic Functions
sinh x
tanh x 
,
cosh x
1
cosechx 
,
sinh x
1
sechx 
cosh x
cosh x
1
coth x 

sinh x
tanh x
Equivalences
Main page
cos   i sin   ei
cos i  cosh and
sin i  i sinh 
cosh i  cos and
sinh i  i sin 
Complex
numbers:
Hyperbolic
Functions
Sine & Cosine Functions
in Exponential form




1 i
e  e i and
2
1 i
sin 
e  e  i
2i
cos 
Eulers formula

Complex numbers
That’s all folks!
Main page