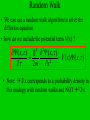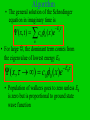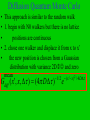Download Diffusion Quantum Monte Carlo

Time-dependent
Schrodinger Equation
• Numerical solution of the time-independent
equation is straightforward
• constant energy solutions do not require us to make
time discrete
• how would we solve the time-dependent equation?
• Naïve approach would be to produce a grid in the
x-t plane
• tn=t0+n t ; xs=x0+s x ; (x,t) => (xs,tn)
Algorithms
• One approach treats the real and imaginary parts
of  separately
• this algorithm ensures that the total probability
remains constant
 ( x , t )  R ( x, t )  i I ( x , t )
• The Schrodinger equation becomes (=1)
dR( x, t )
 H op I ( x, t )
dt
dI ( x, t )
  H op R( x, t )
dt
Algorithm
• Numerical solution of these equations is based on
1
R( x, t  t )  R ( x, t )  H op I ( x, t  t ) t
2
3
1
I ( x, t  t )  I ( x, t  t )  H op R ( x, t ) t
2
2
• The probability density is conserved if we use
1
1
P( x, t )  R( x, t )  I ( x, t  t ) I ( x, t  t )
2
2
1
1
2
P( x, t  t )  R( x, t  t ) R( x, t )  I ( x, t  t )
2
2
2
Initial Wavefunction
• Consider a Gaussian wave packet
1/ 4
 1 
( x,0)  
2 
 2 
ik0 ( x  x0 )
e

e
( x  x0 )2
4 2
• The expectation value of the initial velocity
is <v>=p0/m= k0/m
• in the simulation set m= =1
tdse1
Random Walk Monte Carlo
• We now consider a Monte Carlo approach
based on the relationship of the Schrodinger
equation to a diffusion process in imaginary
time
• if we substitute =it/ into the timedependent Schrodinger equation for a free
particle (V=0) we have
 ( x, t )
  ( x, t )

2

2m x
2
2
Diffusion Monte Carlo
• Compare with the classical diffusion equation
P( x, t )
 P ( x, t )
D
2
t
x
2
 ( x, t )
  ( x, t )

2

2m x
2
2
• Can interpret  as a probability density with a
diffusion constant D=2/2m
Random Walk
• We can use a random walk algorithm to solve the
diffusion equation
• how do we include the potential term V(x) ?
 ( x, )
  ( x,  )


V
(
x
)

(
x
,

)
2

2m x
2
2
• Note: x corresponds to a probability density in
this analogy with random walks and NOT 2x
Algorithm
• The general solution of the Schrodinger
equation in imaginary time is
( x, t )   cnn ( x)e
 En
n
• For large , the dominant term comes from
the eigenvalue of lowest energy E0
 ( x,  )  c00 ( x)e
 E0
• Population of walkers goes to zero unless E0
is zero but is proportional to ground state
wave function
Algorithm
• We can measure E0 from an arbitrary reference
energy Vref and we can adjust Vref until a steady
population of walkers is obtained
2
 ( x, )
 2  ( x,  )

 V ( x)  Vref   ( x,  )
2

2m x
Using
( x, )  c00 ( x)e
It is easy to show
E0
 ( E0 Vref )
V ( x)( x, )dx


 ( x, )dx
Random Walkers
E0
V ( x)( x, )dx


 ( x, )dx
• Hence
E0
nV ( x )

 V 
n
i
i
i
• ni is the density of walkers at xi
Possible Algorithm
• 1. Place N0 walkers at the initial set of positions xi
• 2. compute the reference energy Vref= Vi/N0
• 3. randomly move a walker to the right or left by
fixed step length s
•
s is related to  by (s)2=2D 
•
if m= =1, then D=1/2
• 4. compute V= [V(x)-Vref] and a random number
r in the interval [0,1]
• if V>0 and r < V , then remove the walker
• if V<0 and r < -V , then add a walker at x
• 5. Repeat 3. and 4. for all N0 walkers
Possible Algorithm
• Compute the new number of walkers N
• compute <V>
• The new reference potential is
a
Vref  V  
( N  N0 )
N 0 
• The constant a is adjusted so that N remains
approximately constant
• 6. Repeat steps 3-5 until the ground state energy
estimate <V> has small fluctuations
Program
• Input parameters are:
• number of initial walkers N0, number of Monte
Carlo steps mcs, and step size ds
• consider a harmonic oscillator potential
• V(x)= (1/2)kx2
N0 =50
mcs=1000
ds=0.1
qmwalk
Diffusion Quantum
Monte Carlo
• Introduce the concept of a Green’s function
or propagator defined by
 ( x,  )   G ( x, x,  ) ( x, 0)dx
• G propagates the wave function from time t=0 to
time 
• similar to electrostatics:
( r ) 
1
4 0
 (r )
 r  r
d r
3
Diffusion Quantum
Monte Carlo
 ( x,  )   G ( x, x,  ) ( x, 0)dx
• Operate on both sides with / and then with
(Hop-Vref)
G
 ( H op  Vref )G
• hence G satisfies

• With solution
G ( )  e
 ( H op Vref )
G ( )  e
 ( H op Vref )
• But Hop=Top + Vop and [Top,Vop] 0
• only for short  can we factor the exponential
G ( )  e
1
 (Vop Vref ) 
2
e
Top 
e
1
 ( Vop Vref ) 
2
 Gbranch / 2Gdiff Gbranch / 2
Gdiff  e
Top 
Gbranch / 2  e
1
 (Vop Vref ) 
2
Gdiff  e
Gdiff

Top 
 Top Gdiff 
Gbranch / 2  e
2
1
 (Vop Vref ) 
2
 Gdiff
2
2m x
2
Gbranch / 2
 (Vref  Vop )Gbranch / 2

Gdiff ( x, x,  )  (4 D )
Gbranch ( x, x,  )  e
1/ 2
D
e
2
2m
 ( x  x )2 / 4 D
1
 ( V ( x ) V ( x )Vref ) 
2
Diffusion Quantum Monte Carlo
• This approach is similar to the random walk
• 1. begin with N0 walkers but there is no lattice
•
positions are continuous
• 2. chose one walker and displace it from x to x’
•
the new position is chosen from a Gaussian
distribution with variance 2D and zero
mean
1/ 2  ( x  x )2 / 4 D
Gdiff ( x, x,  )  (4 D )
e
Diffusion Quantum Monte Carlo
• 3. Weight the configuration x by
w( x  x,  )  e
•
•
•
1
 V ( x ) V ( x ) Vref
2

 

For example, if w~2, we should have two
walkers at x where previously there was one
to implement this weighting(branching) correctly
we must make an integer number of copies that
is equal on average to w
take the integer part of w+r where r is a random
number in the unit interval
Diffusion Quantum Monte Carlo
• 4. Repeats steps 2 and 3 for all random walkers
(the ensemble) and create a new ensemble
• one iteration of the ensemble is equivalent to
performing the integration
qmwalk
 ( x,  )   G ( x, x,  ) ( x,    ) dx
• The quantity (x,) will be independent of the
original ensemble (x,0) if a sufficient number of
Monte Carlo steps are used.
• We must keep N(), the number of configurations
at time , close to N0