Download A cyclic quadrilateral

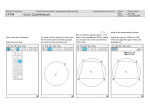
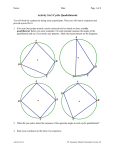
Name: ____________________________________ Date: __________________________
Geometry Unit 10 Day 3 Circle segments
A cyclic quadrilateral is a quadrilateral whose vertices all lie on a circle.
It doesn't matter if the angles or sides are parallel or congruent or none of the above. If
we can draw a circle that connects all the vertices of that quadrilateral, it's cyclic. No
questions asked.
Which of the following quadrilaterals are cyclic?
Try to draw a
circle
around each!!!
Let’s look at a cyclic quadrilateral (inscribed quadrilateral)
Use what we learned about inscribed angles and find the measures of angles x and y.
What can we conclude about the angles in a cyclic quadrilateral?
Are all circles similar?
1) Find the translation rule and the scale factor
of the dilation.
2) Complete the proof.
Given: Circle C with center C and radius r.
Circle D with center D and radius s.
Prove: Circle C is similar to circle D.
To prove similarity, show that there is a sequence of similarity transformations that
maps circle C to circle D.
A) First, transform circle C with a ___________________ along vector _________ .
Under this __________________, C’ maps onto point ______.
B) Now transform circle C’ with the dilation that has the center of dilation at ______,
and scale factor of ________. Circle C’ consists of all points at distance ______
from point D. After the dilations, the image of circle C’ consists of all points at
distance ______ from point D. But these are exactly the points that form circle D.
Since translations and dilations are _______________________________, you
can conclude that ________________________________________.