Geometry Lecture Notes
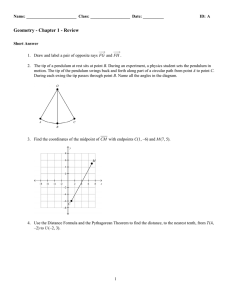
... common, i.e. l intersects m iff there exists A such that A is on l and A is on m. In this situation we say that the lines l and m intersect at A. A set of lines, all of which contain a point A are said to be concurrent. Definition The points in a figure are collinear if there exists a line containin ...
... common, i.e. l intersects m iff there exists A such that A is on l and A is on m. In this situation we say that the lines l and m intersect at A. A set of lines, all of which contain a point A are said to be concurrent. Definition The points in a figure are collinear if there exists a line containin ...
Tangent circles in the hyperbolic disk - Rose
... Other geometries use some of these same axioms, but they may not use all of them. Axioms are statements that are universally accepted as true without requiring a proof. Hyperbolic geometry follows the first four of these axioms, but not the fifth axiom, the Parallel Postulate. One negation of the Pa ...
... Other geometries use some of these same axioms, but they may not use all of them. Axioms are statements that are universally accepted as true without requiring a proof. Hyperbolic geometry follows the first four of these axioms, but not the fifth axiom, the Parallel Postulate. One negation of the Pa ...
My High School Math Note Book, Vol. 1
... I kept (and still do today) small notebooks where I collected not only mathematical but any idea I read in various domains. These two volumes reflect my 1973-1974 high school studies in mathematics. Besides the textbooks I added information I collected from various mathematical books of solved probl ...
... I kept (and still do today) small notebooks where I collected not only mathematical but any idea I read in various domains. These two volumes reflect my 1973-1974 high school studies in mathematics. Besides the textbooks I added information I collected from various mathematical books of solved probl ...
Pseudo-integrable billiards and arithmetic dynamics
... Billiards in domains bounded by several confocal quadrics, without singular points where tangents form a reflex angle, were already studied by the authors: their periodic trajectories are described in [DR2004, DR2006a] while their topological properties are discussed in [DR2009]. In this work, we ar ...
... Billiards in domains bounded by several confocal quadrics, without singular points where tangents form a reflex angle, were already studied by the authors: their periodic trajectories are described in [DR2004, DR2006a] while their topological properties are discussed in [DR2009]. In this work, we ar ...
Non Euclidean Geometry
... Euclid (ca 300 BC) The first to write down the postulates for what is now known as Euclidean geometry. He was associated with the famous School of Alexandria. Archimedes (ca 225 BC) Pliny called him “the God of Mathematics”. He was also associated with the School of Alexandria. His name is now assoc ...
... Euclid (ca 300 BC) The first to write down the postulates for what is now known as Euclidean geometry. He was associated with the famous School of Alexandria. Archimedes (ca 225 BC) Pliny called him “the God of Mathematics”. He was also associated with the School of Alexandria. His name is now assoc ...
Course Notes - Mathematics
... following diagram with the numbers 1 through 7 so that the columns of the above problem correspond to the triples of points in the diagram below that lie on a common line or circle. ...
... following diagram with the numbers 1 through 7 so that the columns of the above problem correspond to the triples of points in the diagram below that lie on a common line or circle. ...
Chapter 3
... called Axioms of the geometry. Two Axioms we require are that each pair of points P, Q in P belongs to at least one line l in L, and that each line l in L contains at least two elements of P. We can impose further geometric structure by adding other axioms to this definition as the following example ...
... called Axioms of the geometry. Two Axioms we require are that each pair of points P, Q in P belongs to at least one line l in L, and that each line l in L contains at least two elements of P. We can impose further geometric structure by adding other axioms to this definition as the following example ...