* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 8-5 Angle Bisector Theorem
Survey
Document related concepts
Transcript
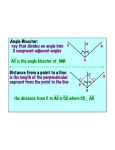
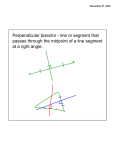
Name: ____________________________________ Geometry Per _____ 8-5 Notes Date: ___________ Angle Bisector Theorem Learning Goals: (1) How can we use the angle bisector theorem to find missing segments in a given triangle? Before we begin: Factoring Practice How to factor polynomials using sum and product: How to factor and solve polynomials using sum and product: Steps The standard form for a quadratic is ax2 + bx + c = 0 1. We are looking for factors of C (numbers that multiply to the last number) that also have the sum of b (add to the middle number) 2. List your factors of c and identify which pair add to b 3. Set up your parenthesis to set up your factors appropriately. Example Together ex 1) x2 + 5 x + 6 = 0 1. C = 6 Factors of 6: 1&6 2&3 -1 & -6 -2 & -3 2. Which of those pairs add to 5? 2&3 3. (x+2)(x+3) = 0 x = -2 x = -3 Example Together ex 2) -12 -x + x2 = 0 You Try! ex 3) x2 + 7 x + 10 = 0 Together! What type of segment is AP? How do you know? With a partner! What do all three diagrams above have in common? Do you notice any relationships that exist? ANGLE BISECTOR THEOREM: An _______________ of a vertex angle in a triangle divides the ___________ side in two segments that are _______________ to the other two sides of the triangle. LET’S TRY SOME: ̅̅̅̅ is the angle bisector of∠𝐵𝐴𝐶, 𝐴𝐷 ̅̅̅̅divides the sides of the triangle proportionally. 1. Given that 𝐴𝐷 This proportion can be representd as, *Is is true that AB * DC = AC * BD? Explain why. 2. Look at the measurements given below to determine if ̅̅̅̅ 𝐴𝐻 is or is not an angle bisector. Explain your reasoning. Stations Practice - Work Space Stations Practice - Work Space Stations Practice 1. Find the missing segment length in the triangle below. Explain how you got your answer (i.e., what theorem did you use, etc…) ̅̅ an angle bisector? Justify 2. IS ̅̅ 𝐶𝑆 your answer. 3. Given that ∆𝐴𝐵𝐶~∆𝐷𝐸𝐹, a)What is the ratio of their corresponding medians? b) What is the ratio of their areas? 4 a) Solve for x. b) Using the answer above, solve for CA. 5 Four streets in a town are 6. illustrated in the accompanying diagram. The angle between Poplar Street and Fern is equivalent to the angle between Elm Street and Fern street. If the distance from E to F is 8 miles, F to P is 10 miles, and other distances are indicated below, how far apart is are points M and P? Name: ____________________________________ Geometry Per. _____ 8-5 Homework Date: ___________ 1. Use the angle bisector theorem to find the missing side length of the segment in the triangle below: CA = 12, CD = 6, BA = 15, DB = ? 2. What is the length of Wx in the triangle below, given that WZ = 24, ZY = 12, XY = 15. 3. In the diagram below of , D is the midpoint of , O is the midpoint of If AC = 20, AT = 36, and CT = 22, what is the perimeter of parallelogram CDOG? 1) 42 2) 50 3 ) 78 ) 4) 32 , and G is the midpoint of . 4. Factor: 8y3z + 16xy 5. Solve: z2 – 2z = 24 6. Is AD an angle bisector? Explain why or why not. Follow up: can we identify a shortcut method that would allow us to conclude that ∆𝐴𝐵𝐷 ~∆𝐴𝐶𝐷? 7. Using properties of similarity and specific vocabulary we’ve learned in this unit, describe why the two triangles below are similar to each other.