* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lesson 5-2 Perpendicular and Angle Bisectors
Steinitz's theorem wikipedia , lookup
Cartesian coordinate system wikipedia , lookup
Rational trigonometry wikipedia , lookup
Atiyah–Singer index theorem wikipedia , lookup
Perceived visual angle wikipedia , lookup
Integer triangle wikipedia , lookup
Trigonometric functions wikipedia , lookup
Riemann–Roch theorem wikipedia , lookup
History of trigonometry wikipedia , lookup
Noether's theorem wikipedia , lookup
Euclidean geometry wikipedia , lookup
Four color theorem wikipedia , lookup
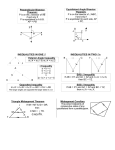
Lesson 5-2: Perpendicular and Angle Bisectors Goal: Use angle bisectors and perpendicular bisectors to prove triangles congruent or find missing measures. Key Words: Theorem 5.3: Example 1: Use the Angle Bisector Theorem In the diagram, 𝐸𝐺 bisects ∠𝐶𝐸𝐹. Prove that ∆𝐶𝐷𝐸 ≅ ∆𝐹𝐷𝐸. Statements Reasons 1. 𝐸𝐺 bisects ∠𝐶𝐸𝐹 Given 2. ∠𝐶𝐸𝐷 ≅ ∠𝐹𝐸𝐷 Def. of angle bisector 3. ∠𝐷𝐶𝐸 𝑎𝑛𝑑∠𝐷𝐹𝐸 are right ∠′ 𝑠 Given 4. ∠𝐷𝐶𝐸 ≅ ∠𝐷𝐹𝐸 All right angles are ≅. 5. 𝐷𝐶 ≅ 𝐷𝐹 Angle Bisector Theorem 6. ∆𝐶𝐷𝐸 ≅ ∆𝐹𝐷𝐸 AAS Theorem 5.4: Example 2: Use Perpendicular Bisectors Use the diagram to find GH. 3𝑥 + 2 = 5𝑥 − 12 2 = 2𝑥 − 12 14 = 2𝑥 14 2 = 2𝑥 2 7=𝑥 by the Perpendicular Bisector Theorem GH = KH. Subtract 3x from both sides. Subtract 12 from both sides. Divide both sides by 2. Simplify. 𝐺𝐻 = 3 7 + 2 = 21 + 2 = 23 Your Turn: 𝑥 + 3 = 2𝑥 + 1 4𝑥 = 𝑥 + 15 2𝑥 + 5 = 𝑥 + 10 2=𝑥 3𝑥 = 15 𝑥=5 𝐹𝐻 = 2 + 3 = 5 𝑥=5 𝐸𝐹 = 2 5 + 5 = 15 𝑀𝐾 = 5 + 15 = 20 Example 3: Using the Perpendicular Bisector Theorem Can you prove that ∆𝑀𝑆𝑇 is an isosceles triangle if 𝑀𝑁 is only known to be a bisector of 𝑆𝑇. No, if 𝑀𝑁 is not known to be perpendicular we can not conclude that 𝑀𝑇 and 𝑀𝑆 are congruent. Checkpoint: equidistant Perpendicular bisector 𝒙 + 𝟏 = 𝟐𝒙 − 𝟏 16 𝟐=𝒙 𝑬𝑭 = 𝟐 + 𝟏 = 𝟑 𝟓𝒙 = 𝟑𝒙 + 𝟖 12 𝒙=𝟒 𝑸𝑹 = 𝟓(𝟒) = 𝟐𝟎 Assignment: p 296 – 298 #’s 6 – 34 even