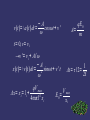* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Wideroe accelerator Concept Analysis
Survey
Document related concepts
Compact Muon Solenoid wikipedia , lookup
Photoelectric effect wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Future Circular Collider wikipedia , lookup
Electron scattering wikipedia , lookup
Crookes tube wikipedia , lookup
Transcript
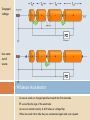
WIDEROE ACCELERATOR CONCEPT (IN A BOTTLE) Presented by: Stephen, Leon, Daichi, Stefan Outline of Presentation Stephen Aims and goals Wideroe Accelerator Assumptions and Questions Leon Limits and Parameters Frequency limit Size of bottle Daichi Stefan Maths behind Accelerator Results using MATLAB plots Aims and goals Investigate a simple linear accelerator Design the accelerator into a standard wine bottle Design to get the highest energy particles possible Cathode Vacuum pump High Potential Difference Anode Wine bottle Homemade wine bottle CRT Electrons are accelerated by a high potential difference (kV) from cathode to anode. The blue diffusion given out by ‘Cathode rays’ are caused by fast moving electrons exciting the gas molecules left in the bottle or striking the glass and causing the excited molecules to decay emitting out photons of bluish wavelength. http://www.instructables.com/id/DIY-Electron-Accelerator-A-Cathode-Ray-Tube-in-a-/ - Extracted 23/01/2014 Swapped voltage Ions come out of source Wideroe Accelerator • Ion source sends our charged particles towards the first electrode • RF source flips the sign of the electrodes • Ions are at constant velocity in drift tubes as voltage flips • When Ions reach other side they are accelerated again and cycle repeats Aim: Design a Linear Accelerator in a Bottle Assumptions: Bottle's length is ~ 50 cm Vacuum required ~ 1×10−3 torr Questions to be discovered How much energy can we get by changing these parameters: f = frequency of RF U = Amplitude of alternating current m = mass of particles Length of drift tubes to be as small as possible Limits and Parameters Voltage has to be in kV range Length of drift tubes Cannot exceed breakdown voltage 3.0 MV/m – Air 20-40 MV/m – High quality vacuum Frequency of RF voltage < 10MHz Why the frequency limit? It can be seen that our system is like a parallel plate capacitor. Where dQ = C(v)*dV And C = (A/d) εr ε0 This presents another issue: The fact that our ‘d’ is increasing as we make our tube longer, this decreases the capacitance. The frequency limit can be shown by the simple RC circuit. The transient response is shown on the bottom left. What we see is τ = R*C, where τ is the ‘time constant’ of the capacitor. Due to this, it can be seen that at high frequencies the material doesn’t have enough time to fully charge to the given voltage. Size, an issue? • • As the length of each drift tube and the gap is increasing for every iteration along electron path. It can be seen that the structure will get very large, expensive and difficult to build, extremely fast. So what we’ve thought of is a systematic concept which basically involves instead of increasing the lengths incrementally but rather modulating the initial RF carrier to keep in phase with the accelerating electron. Mathematics Behind the Design ➲ Constant velocity in the tube V = V max sinωt E i = iqU max sinψ 0 V = potential difference E i = energy at ith tube 1 2 E i = mv i 2 ➲ Equate the energy to solve for v. Length of the Tube √ 2iqV max sinψ 0 vi= m The time that the particle travel: T = 1 2 2f T = Period, f = frequency ➲ √ 2iqV max sinψ 0 1 → l i= m 2f Length of the Gap ➲ This time, velocity is not constant E= E 0 sinωt But also... qE= F = ma qE 0 sinωt a (t)= m E= Electric field −A v (t)= a (t)dt = cosωt+ v ' ω qE 0 A= m ∫ t= 0, v= v i →v ' = v i + A/ ω −A ∫ x (t)= v (t)dt = 2 sinωt+ v ' t ω qV max Δx= x i = l i + 2 4mπf x i 1 Δt = τ / 2= 2f V max E 0= xi qV max x − l i xi− 2= 0 4mπf 2 i √ qV max l i± l + 2 mπf → xi = 2 2 qV max l i± l i + 2 n n mπf L= ∑0 + ∑1 l i 2 2 i √ √ √ qV max n qV max 2 ∑ 2 + 1 (3l i + l i + 2) mπf mπf = 2 Varying Voltage of RF generator (1) 5 9 Energy in tube vs Number of drift tubes x 10 kV 8 1 10 25 40 70 100 7 Particle energy in tube (eV) RF frequency = 5MHz 6 5 4 3 2 1 0 1 2 3 4 5 6 Number of tubes 7 8 9 10 Varying Voltage of RF generator (2) Length vs Number of drift tubes 2 10 RF frequency = 5MHz 1 Length (m) 10 0 10 kV 1 10 25 40 70 100 -1 10 -2 10 1 2 3 4 5 6 Number of tubes 7 8 9 10 Varying frequency of RF generator (1) 5 2.2 Energy in tube vs Number of drift tubes x 10 MHz kV 0.003 2 Particle energy in tube (eV) 1.8 RF Amplitude = 25 0.01 0.1 1 10 100 1000 1.6 1.4 1.2 1 0.8 0.6 0.4 0.2 1 2 3 4 5 6 Number of tubes 7 8 9 10 Varying frequency of RF generator (2) Length vs Number of drift tubes 5 10 RF Amplitude = 25 kV 4 10 MHz 3 10 2 Length (m) 10 1 10 0 10 -1 10 -2 10 -3 10 1 2 3 4 5 6 Number of tubes 7 8 9 10 Final Idea! 5 Energy in tube vs Number of drift tubes Length vs Number of drift tubes 5 2 4.5 1.8 4 1.6 3.5 1.4 3 Length (m) Particle energy in tube (eV) 2.2 x 10 1.2 1 2.5 2 0.8 1.5 0.6 1 0.4 0.2 0.5 X: 2 Y: 4.207e+004 1 2 3 4 5 6 Number of tubes 7 8 9 10 0 X: 2 Y: 0.514 1 2 3 4 5 6 Number of tubes 7 8 9 10 Questions