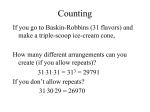Download 6.1 Logic Statements or Propositions Negation

6.1 Logic
Logic is not only the foundation of mathematics, but also is
important in numerous fields including law, medicine,
and science. Although the study of logic originated in
antiquity, it was rebuilt and formalized in the 19th and
early 20th century. George Boole (Boolean algebra)
introduced mathematical methods to logic in 1847 while
Georg Cantor did theoretical work on sets and
discovered that there are many different sizes of infinite
sets.
Statements or Propositions
„
„
A proposition or statement is a declaration which is either true or false.
Some examples:
„
„
„
„
2+2 = 5 is a statement because it is a false declaration.
Orange juice contains vitamin C is a statement that is
true.
Open the door. This is not considered a statement since
we cannot assign a true or false value to this sentence.
It is a command, but not a statement or proposition.
Negation
„
The negation of a statement, p , is “not p”
and is denoted by ┐ p
Truth table:
p
┐p
T
F
F
T
„
If p is true, then its negation is false. If p is false, then its negation is true.
„
„
„
„
1
Disjunction
„
„
„
A disjunction is of the form p V q and is read p or q.
Truth table for disjunction:
p
q
pVq
„
„
T
T
F
F
„
A disjunction is true in all cases except when both p and q are false.
„
„
„
T
F
T
F
T
T
T
F
Conjunction
„
„
A conjunction is only true when both p and q are true. Otherwise, a
conjunction of two statements will be false:
Truth table:
p
q
T
T
F
F
T
F
T
F
p
∧
q
T
F
F
F
Conditional statement
„
„
„
„
„
„
„
„
„
„
To understand the logic behind the truth table for the conditional statement, consider
the following statement.
“If you get an A in the class, I will give you five bucks.”
Let p = statement “ You get an A in the class”
Let q = statement “ I will give you five bucks.”
Now, if p is true (you got an A) and I give you the five bucks, the truth value of
p
q is true. The contract was satisfied and both parties fulfilled the agreement.
Now, suppose p is true (you got the A) and q is false (you did not get the five bucks).
You fulfilled your part of the bargain, but weren’t rewarded with the five bucks.
So p
q is false since the contract was broken by the other party.
Now, suppose p is false. You did not get an A but received five bucks anyway. (q is
true) No contract was broken. There was no obligation to receive 5 bucks, so truth
value of p
q cannot be false, so it must be true.
Finally, if both p and q are false, the contract was not broken. You did not receive the
A and you did not receive the 5 bucks. So p
q is true in this case.
2
Truth table for conditional
„
p
q
T
T
F
F
T
F
T
F
p
q
T
F
T
T
Variations of the conditional
„
Converse:
„
Contrapositive:
„
┐q
The converse of p
q is q
The contrapositive of p
p
q is
┐p
Examples
„
Let p = you receive 90%
Let q = you receive an A in the course
p
q?
„
If you receive 90%, then you will receive an A in the course.
„
Converse: q
„
„
„
„
p
If you receive an A in the course, then you receive 90%
Is the statement true? No. What about the student who receives a
score greater than 90? That student receives an A but did not
achieve a score of exactly 90%.
3
Example 2
„
„
„
„
„
„
„
„
State the contrapositive in an English sentence:
Let p = you receive 90%
Let q = you receive an A in the course
p
q?
If you receive 90%, then you will receive an A in the course
┐q
┐p
If you don’t receive an A in the course, then you didn’t receive 90%.
The contrapositive is true not only for these particular statements
but for all statements , p and q.
Logical equivalent statements
„
„
„
Show that
p→q
is logically equivalent to
¬p ∨ q
We will construct the truth tables for both sides and determine that
the truth values for each statement are identical.
The next slide shows that both statements are logically equivalent.
The red columns are identical indicating the final truth values of
each statement.
4
6.2 Sets
This section will discuss the
symbolism and concepts of set
theory
Set properties and set notation
„
„
„
„
Definition of set: A set is any collection of objects
specified in such a way that we can determine whether
or not an object is or is not in the collection.
Example 1. Set A is the set of all the letters in the alphabet.
Notation: A = { a, b, c, d, e, …z) We use capital letters to represent
sets. We list the elements of the set within braces. The three dots …
indicate that the pattern continues. We can determine that an
object is or is not in the collection. For example . e
A stands for
“e is an element of , or e belongs to set A” . This statement is true.
The statement “ 3
A is false, since the number 3 is not an
element of set A. The statement “ 3
A” is true.
∈
∈
Null set
„
„
„
Example. What are the real number solutions of the equation?
x2 + 1 = 0
Answer: There are no real number solutions of this equation since
no real number squared added to one can ever equal 0. We
represent the solution as the null set { } or Ø
1
Set builder notation
„
Sometimes it is convenient to represent sets using what is called
set-builder notation. For example, instead of representing the set A,
letters in the alphabet by the roster method, we can use set
builder notation:
x x is letter of the English alphabet
{
„
„
}
means the same as { a , b , c, d, e , …z}
Example two. { x l x2 =9 } = {3 , -3} . This is read as the set of all
such that the square of x equals 9. The solution set consists of the
two numbers 3 and -3.
Subsets
„
„
„
„
⊂
A
B means A is a subset of B. A is a subset of A if every element of A is
also contained in B. For example, the set of integers denoted by
{ …-3, -2, -1, 0, 1, 2, 3, …} is a subset of the set of real numbers.
Formal definition of subset: A ⊂ B means if x
A, the x
B
(null set )is a subset of every set. To verify this statement, let’s use the
definition of subset. “ if x
∅ , then x is an element of A. But since
the null set contains no elements, the statement x is an element of the
null set is false. Hence, we have a conditional statement in which the
premise is false. We know that p
q is true if p is false. Since p is
false, we conclude that the conditional statement is true. That is “ if x
belongs to the null set, then x belongs to set A” is true, which implies that
the null set must be a member of every set. Therefore, the null set is a
subset of every set.
∅
∈
∈
∈
Number of subsets
„
List all the subsets of set A = {bird, cat, dog} For convenience, we
will use the notation A = {b , c, d} to represent set A.
Solution: ∅ is a subset of A. We also know that every set is a subset
of itself so A = {b , c, d } is a subset of set A since every element of
set A is contained within set A.
How many two-element subsets are there?
We have {b, c}, {b, d} , {c, d}
How many one-element subsets? { b} , {c} and {d} .
There is a total of 8 subsets of set A if you count all the listed subsets.
2
Set operations
The union of two sets is the set of all elements formed by combining all
the elements of set A and all the elements of set B into one set.
The symbolism used is The Venn Diagram representing the union of A
and B is the entire region shaded yellow.
A
B
A ∪ B = {x x ∈ A or x ∈ B}
Example of Union
„
The union of the rational numbers with the set of irrational numbers
is the set of real numbers. Rational numbers are those numbers that
can be expressed as fractions, while irrational numbers are numbers
that cannot be represented exactly as fractions, such as 2
Rational numbers
„
a/b, ¾, 2/3 , 0.6
Irrational numbers
such as square root
of two, Pi , square
root of 3
Real numbers: represented by
shaded blue-green region
Intersection of sets A and B
„
„
The intersection of sets A and B is the set of elements that is
common to both sets A and B. It is symbolized as
A ∩ B = { x l x A and x B }
A
„
„
B
Represented by Venn Diagrams:
Intersection
3
Complement of a set
„
„
„
„
To understand the complement of a set, we must first define the universal
set. The set of all elements under consideration is called the universal set.
For example, when discussing numbers, the universal set may consist of
the set of real numbers. All other types of numbers (integers, rational
numbers, irrational numbers ) are subsets of the universal set of real
numbers.
Complement of set A: The complement of a set A is defined as the set
of elements that are contained in U, the universal set, but not contained in
set A. The symbolism for the complement of set A follows:
A’ = { x
U |x
A}
Venn Diagram for complement of set A
Yellow region=
„ all
elements in U that
are neither in A or
B.
„
A
Elements of set
B that are not
in A
The complement of set A is
represented by the regions
that are colored blue and
yellow. The complement of set
A is the region outside of the
white circle representing set A.
A’
A’
B
4
6.3 Basic Counting Principles
In this section, we will see how set
operations play an important role in
counting techniques.
Opening example
†
†
†
To see how sets play a role in counting, consider the following
example.
In a certain class, there are 23 majors in Psychology, 16
majors in English and 7 students who are majoring in
both Psychology and English. If there are 50 students in
the class, how many students are majoring in neither of
these subjects?
B) How many students are majoring in Psychology
alone?
Solution:
†
We introduce the following principle of
counting that can be illustrated using a
Venn-Diagram.
†
N( A U B) = n(A) + n(B) – n(A
†
This statement says that the number of
elements in the union of two sets A and
B is the number of elements of A added
to the number of elements of B minus
the number of elements that are in both
A and B.
∩
B)
A
B
1
Do you see how the numbers of each region are obtained from the given information in the
problem? We start with the region represented by the intersection of Psych. And English
majors (7). Then, because there must be 23 Psych. Majors, there must be 16 Psych majors
remaining in the rest of the set. A similar argument will convince you that there are 9
students who are majoring in English alone.
7 students in this region
Both
Psych
and
English
N(P U E) =
n(P)+n(E)-n(P
9 students
in this
region
Psychology majors
= 32
∩ E)
23 + 16 – 7
English majors
16 students
here
A second problem
† A survey of 100 college faculty who exercise regularly
found that 45 jog, 30 swim, 20 cycle, 6 jog and swim, 1
jogs and cycles, 5 swim and cycle, and 1 does all three.
How many of the faculty members do not do any of
these three activities? How many just jog?
† We will solve this problem using a three-circle Venn
Diagram in the accompanying slides.
We will start with the intersection of all three circles. This region represents the number of faculty
who do all three activities (one). Then, we will proceed to determine the number of elements in each
intersection of exactly two sets
J =joggers
1 does all 3
S=swimmers
C=Cyclists
2
Solution:
†
Starting with the intersection of all
three circles, we place a 1 in that
region (1 does all three). Then we
know that since 6 jog and swim so
5 faculty remain in the region
representing those who just jog and
swim. Five swim and cycle, so 4
faculty just swim and cycle but do
not do all three. Since 1 faculty is in
the intersection region of joggers
and cyclists, and we already have
one that does all three activities,
there must be no faculty who just
jog and cycle.
Multiplication principle The tree diagram illustrates the 24 ways to get
dressed.
†
†
To illustrate this principle, let’s start
with an example. Suppose you have
4 pairs of trousers in your closet, 3
different shirts and 2 pairs of shoes.
Assuming that you must wear
trousers (we hope so!), a shirt and
shoes, how many different ways can
you get dressed? Let’s assume the
colors of your pants are black, grey,
rust, olive. You have four choices
here. The shirt colors are green,
marine blue and dark blue. For each
pair of pants chosen (4) you have
(3) options for shirts. You have 12
= 4*3 options for wearing a pair of
trousers and a shirt. Now, each of
these twelve options, you have two
pair of shoes to choose from (Black
or brown). Thus, you have a total of
4*3*2 = 24 options to get dressed.
Generalized multiplication principle
† Suppose that a task can be performed using
two or more consecutive operations. If the first
operation can be accomplished in m ways and
the second operation can be done in n ways,
the third operation in p ways and so on, then
the complete task can be performed in m·n·p
… ways. .
3
More problems…
†
How many different ways can a team consisting of 28 players
select a captain and an assistant captain?
†
Solution: Operation 1: select the captain. If all team members
are eligible to be a captain, there are 28 ways this can be
done.
†
Operation 2. Select the assistant captain. Assuming that a
player cannot be both a captain and assistant captain, there
are 27 ways this can be done, since there are 27 team
members left who are eligible to be the assistant captain.
†
Then, using the multiplication principle there are (28)(27)
ways to select both a captain and an assistant captain. This
number turns out to be 756.
Final example
†
A sportswriter is asked to rank 8
teams in the NBA from first to last.
How many rankings are possible?
† Solution:
We will use 8 slots that
need to be filled. In the first slot, we will
determine how many ways to choose the
first place team, the second slot is the
number of ways to choose the second place
team and so on until we get to the 8th place
team. There are 8 choices that can be made
for the first place team since all teams are
eligible. That leaves 7 choices for the second
place team. The third place team is
determined from the 6 remaining choices
and so on.
8
†
7
6
5
4
3
2
1
Total is the product of 8(7)…1 = 40320
4
6.4 Permutations and
combinations
For more complicated problems, we will need to
develop two important concepts: permutations and
combinations. Both of these concepts involve what is
called the factorial of a number.
Definition of n factorial (!)
†
†
†
n! = n(n-1)(n-2)(n-3)…1
For example, 5! = 5(4)(3)(2)(1)=120
0! = 1 by definition.
†
†
How it is used in counting: Example. The simplest
protein molecule in biology is called vasopressin
and is composed of 8 amino acids that are
chemically bound together in a particular order.
The order in which these amino acids occur is of
vital importance to the proper functioning of
vasopressin. If these 8 amino acids were placed in
a hat and drawn out randomly one by one, how
many different arrangements of these 8 amino
acids are possible?
Solution: Let A,B,C,D,E,F,G,H symbolize the 8
amino acids. They must fill 8 slots: ___ ___ ___
___ ___ ___ ___ ___ . There are 8 choices for the
first position, leaving 7 choices for the second slot,
6 choices for the third slot and so on. The number
of different orderings is
8(7)(6)(5)(4)(3)(2)(1)=8! =40,320.
†
†
Example continued:
†
†
Of the 40,320 possible orderings of the 8 amino acids, the human body
can use just one. What is the probability that, by random chance
alone with no outside interference, the correct order occurs. We
will discuss probability in the next chapter, but here is the answer:
Probability of correct order is
, an extremely unlikely event.
1
40,320
†
For more complicated biological molecules, such as hemoglobin, with
many more amino acids, the probability that the correct order occurs
by random chance alone is extremely small (close to zero!) which
raises questions in some scientists’ minds of just how such molecules
came to be formed by random chance. Some have concluded that their
creation was not due to random chance but by intelligent design
which raises still more questions that cannot be completely answered.
1
Two problems illustrating combinations and
permutations.
Consider the following two problems:
1) Consider the set { p , e , n} How many two-letter “words”
(including nonsense words) can be formed from the members
of this set?
We will list all possibilities: pe, pn, en, ep, np, ne , a total of 6.
2)
3)
Now consider the set consisting of three males: {Paul, Ed,
Nick} For simplicity, we will denote the set { p, e, n} How
many two-man crews can be selected from this set?
Answer: pe (Paul, Ed), pn (Paul, Nick) and en (Ed, Nick) and
that is all!
Difference between permutations and
combinations
† The difference between the two problems is this:
†
†
†
Both problems involved counting the numbers of arrangements
of the same set {p , e , n}, taken 2 elements at a time,
without allowing repetition. However, in the first problem, the
order of the arrangements mattered since pe and ep are
two different “words”. In the second problem, the order did
not matter since pe and ep represented the same two-man
crew. So we counted this only once.
The first example was concerned with counting the number of
permutations of 3 objects taken 2 at a time.
The second example was concerned with the number of
combinations of 3 objects taken 2 at a time
Permutations
The notation P(n,r) represents the number of permutations
(arrangements) of n objects taken r at a time when r is less
than or equal to n. In a permutation, the order is important.
In our example, we have P(3,2) which represents the number of
permutations of 3 objects taken 2 at a time.
In our case, P(3,2) = 6 = (3)(2)
In general, P(n,r) = n(n-1)(n-2)(n-3)…(n-r+1)
2
More examples
Use the definition P(n,r) = n(n-1)(n-2)(n-3)…(n-r+1)
†
†
†
†
†
†
Find P(5,3)
Here, n = 5 and r = 3 so we have P(5,3) = (5)(5-1)5-3+1) =
5(4)3 = 60. This means there are 60 arrangements of 5 items taken 3
at a time.
Application: How many ways can 5 people sit on a park bench if the
bench can only seat 3 people?
Solution: Think of the bench as three slots ___ ___ ___ .
There are five people that can sit in the first slot, leaving four remaining
people to sit in the second position and finally 3 people eligible for the
third slot. Thus, there are 5(4)(3)=60 ways the people can sit. The
answer could have been found using the permutations formula: P(5,3)
= 60, since we are finding the number of ways of arranging 5 objects
taken 3 at a time.
P(n,n)= n(n-1)(n-2)…1
†
Find P(5,5) , the number of
arrangements of 5 objects taken 5
at a time.
Answer: P(5,5) = 5(5-1)…(5-5+1)
= 5(4)(3)(2)(1)=120.
Application: A bookshelf has space
for exactly 5 books. How many
different ways can 5 books be
arranged on this bookshelf?
†
___ ___ ___ ___ ___ Think of 5
slots, again. There are five choices
for the first slot, 4 for the second
and so on until there is only 1
choice for the final slot. The answer
is 5(4)(3)(2)(1)
which is the same as P(5,5) = 120.
†
†
Combinations
†
†
†
†
†
†
In the second problem, the number of 2 man crews that can be
selected from {p,e ,n} was found to be 6. This corresponds to
the number of combinations of 3 objects taken 2 at a time or
C(3,2). We will use a variation of the formula for permutations
to derive a formula for combinations.
Consider the six permutations of { p, e, n} which are grouped
in three pairs of 2. Each pair corresponds to one combination
of 2.
pe
pn
en
ep
np
ne, so if we want to find the
number of combinations of 3 objects taken 2 at a time, we
simply divide the number of permutations of 3 objects taken 2
at a time by 2 (or 2!)
P(3, 2)
We have the following result: C(3,2) =
2!
3
Generalization
†
General result: This formula gives the number of subsets of
size r that can be taken from a set of n objects. The order of
the items in each subset does not matter.
C (n, r ) =
P (n, r ) n(n − 1)(n − 2)...( n − r + 1)
=
r!
r (r − 1)(r − 2)...1
Examples
†
†
Find C(8,5)
Solution: C(8,5) =
†
2. Find C(8,8)
†
Solution: C(8,8) =
P(8,5) 8(7)(6)(5)(4) 8(7)(6)
=
=
= 8(7) = 56
5!
5(4)(3)(2)(1) 3(2)(1)
P (8,8) 8(7)(6)(5)(4)(3)(2)(1)
=
=1
8!
8(7)(6)(5)(4)(3)(2)(1)
Combinations or Permutations?
†
†
†
1. In how many ways can you
choose 5 out of 10 friends to
invite to a dinner party?
Solution: Does the order of
selection matter? If you choose
friends in the order A,B,C,D,E
or A,C,B,D,E the same set of 5
was chosen, so we conclude
that the order of selection does
not matter. We will use the
formula for combinations since
we are concerned with how
many subsets of size 5 we
can select from a set of 10.
C(10,5) = P (10,5)
10(9)(8)(7)(6)
5!
=
5(4)(3)(2)(1)
=
10(9)(8)(7)
= 2(9)(2)(7) = 252
(5)(4)
4
Permutations or Combinations?
†
How many ways can you arrange 10 books on a bookshelf that
has space for only 5 books?
†
Does order matter? The answer is yes since the arrangement
ABCDE is a different arrangement of books than BACDE. We
will use the formula for permutations. We need to determine
the number of arrangements of 10 objects taken 5 at a time so
we have P(10,5) = 10(9)(8)(7)(6)=30,240
Lottery problem
†
A certain state lottery consists of
selecting a set of 6 numbers
randomly from a set of 49 numbers.
To win the lottery, you must select
the correct set of six numbers. How
many possible lottery tickets are
there?
†
Solution. The order of the numbers
is not important here as long as you
have the correct set of six numbers.
To determine the total number of
lottery tickets, we will use the
formula for combinations and find
C(49, 6), the number of
combinations of 49 items taken 6 at
a time. Using our calculator, we find
that
C(49,6) = 13,983,816
†
5