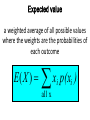Download Expected value a weighted average of all possible values where the

Expected value
a weighted average of all possible values
:
where
the weights are the probabilities of
each outcome
E( X ) 

all x
xi p(xi )
Expected Value
• If a random variable x can have any of the
values x1, x2 , x3 ,…
• the corresponding probabilities of these
values occurring are P(x1), P(x2), P(x3), …
• then the expected value of x is given by
E ( x)  x1  P( x1 )  x2  P( x2 ) 
© 2008 Pearson AddisonWesley. All rights reserved
12-5-2
 xn  P( xn ).
Example: expected value
probability distribution of ER arrivals
x is the number of arrivals in one hour
X
10
11
12
13
14
P(x)
.4
.2
.2
.1
.1
5
 x p( x)  10(.4)  11(.2)  12(.2)  13(.1)  14(.1)  11.3
i
i 1
© 2008 Pearson AddisonWesley. All rights reserved
Try on Excel: Expected Value
Children in third grade were surveyed and told to pick the
number of hours that they play electronic games each
day. The probability distribution is given below.
# of Hours x
Probability P(x)
0
.3
1
.4
2
.2
3
.1
Compute a “weighted average” by multiplying each possible time
value by its probability and then adding the products.
Expected Value
Compute a “weighted average” by multiplying each possible time value by its
probability and then adding the products.
0(.3)  1(.4)  2(.2)  3(.1)  1.1
1.1 hours is the expected value (or the mathematical expectation) of the quantity
of time spent playing electronic games.
© 2008 Pearson AddisonWesley. All rights reserved
12-5-5
Fundamental Counting
Principle
if an event has m possible outcomes and
another independent event has n possible
outcomes, then there are m* n possible outcomes
for the two events together.
EXAMPLE
A student is to roll a die and flip a coin. How many
possible outcomes will there be?
6*2 = 12 outcomes
Fundamental Counting
Principle
For a college interview, Robert has to choose
what to wear from the following:
4 slacks
3 shirts
2 shoes
5 ties.
How many possible outfits does he have to
choose from?
4*3*2*5 = 120 outfits
Permutations
dependent events and order matters
A Permutation is an arrangement of items in a
particular order.
To find the number of Permutations of n items
chosen r at a time, you can use the formula
n!
p 
n r (n  r )!
5!
5!
  5 * 4 * 3  60
5 p3 
(5  3)! 2!
Permutations: dependent events
The number of ways to arrange
the letters ABC: ____ ____ ____
3 ____ ____
Number of choices for second blank? 3 2 ___
Number of choices for third blank?
3 2 1
Number of choices for first blank?
3*2*1 = 6
ABC
ACB
BAC
3! = 3*2*1 = 6
BCA
CAB
CBA
Permutations Examples
A combination lock will open when the
right choice of three numbers (from 1
to 30) is selected. How many different
lock combinations are possible assuming
no number is repeated?
30!
30!

 30 * 29 * 28  24360
30 p3 
( 30  3)! 27!
Permutation Example
From a club of 24 members, a
President, Vice President, Secretary,
Treasurer and Historian are to be
elected. In how many ways can the
offices be filled?
24!
24!


24 p5 
( 24  5)! 19!
24 * 23 * 22 * 21 * 20  5,100,480
Combinations
A Combination is an arrangement of items in which
order does not matter. There are always fewer
combinations than permutations.
To find the number of Combinations of n items
chosen r at a time, you can use the formula
n!
C 
where 0  r  n .
n r r! ( n  r )!
Combinations Example
To play a particular card game, each player is
dealt five cards from a standard deck of 52
cards. How many different hands are
possible?
52!
52!


52 C5 
5! (52  5)! 5!47!
52 * 51 * 50 * 49 * 48
 2,598,960
5* 4* 3* 2*1
Combinations
Practice: A student must answer 3 out of 5
essay questions on a test. In how
many different ways can the
student select the questions?
5!
5! 5 * 4


 10
5 C3 
3! (5  3)! 3!2! 2 * 1
Combinations Examples
A basketball team consists of two centers, five
forwards, and four guards. In how many ways can
the coach select a starting line up of one center,
two forwards, and two guards?
Center:
Forwards:
Guards:
2!
5! 5 * 4
4! 4 * 3
C



10
C


2

6
5 2
2
1
4 C2 
2!3! 2 * 1
2!2! 2 * 1
1!1!
2
C1 * 5 C 2 * 4 C 2
Thus, the number of ways to select the
starting line up is 2*10*6 = 120.