Download The Learnability of Quantum States

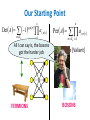
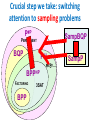
New Computational Insights from
Quantum Optics
Scott Aaronson
Based on joint work with Alex Arkhipov
The Extended ChurchTuring Thesis (ECT)
Everything feasibly
computable in the physical
world is feasibly computable
by a (probabilistic) Turing machine
But building a QC able to factor n>>15 is damn hard!
Can’t CS “meet physics halfway” on this one?
I.e., show computational hardness in more easily-accessible quantum systems?
Also, factoring is a “special” problem
Our Starting Point
Det  A 
 1


sgn 
S n
n
a  
i,
i 1
i
Per A 
n
a  


S n i 1
i,
i
All I can say is, the bosons
In
#P-complete [Valiant]
gotPthe harder job
FERMIONS
BOSONS
So if n-boson amplitudes correspond to permanents…
Can We Use Bosons to Calculate
the Permanent?
That sounds way too good to be true—it would let us
solve NP-complete problems and more using QC!
Explanation: Amplitudes aren’t directly observable.
To get a reasonable estimate of Per(A), you might
need to repeat the experiment exponentially many
times
Basic Result: Suppose there were a polynomial-time
classical randomized algorithm that took as input a
description of a noninteracting-boson experiment, and
that output a sample from the correct final distribution
over n-boson states.
Then P#P=BPPNP and the polynomial hierarchy collapses.
Motivation: Compared to (say) Shor’s algorithm, we
get “stronger” evidence that a “weaker” system can
do interesting quantum computations
Crucial step we take: switching
attention to sampling problems
P#P
SampBQP
PERMANENT
BQP
PH
 X Y…
BPPNP
FACTORING
BPP
3SAT
SampP
Related Work
Valiant 2001, Terhal-DiVincenzo 2002, “folklore”:
A QC built of noninteracting fermions can be efficiently
simulated by a classical computer
Knill, Laflamme, Milburn 2001: Noninteracting bosons
plus adaptive measurements yield universal QC
Jerrum-Sinclair-Vigoda 2001: Fast classical randomized
algorithm to approximate Per(A) for nonnegative A
A. 2011: Generalization of Gurvits’s algorithm that gives
better approximation if A has repeated rows or columns
The Quantum Optics Model
A rudimentary subset of quantum computing, involving
only non-interacting bosons, and not based on qubits
Classical counterpart: Galton’s Board, on display at
the Boston Museum of Science
Using only pegs and noninteracting balls, you probably
can’t build a universal computer—
but you can do some interesting
computations, like generating the
binomial distribution!
The Quantum Version
Let’s replace the balls by identical single photons,
and the pegs by beamsplitters
Then we see strange things like the Hong-Ou-Mandel dip






1
2
1
2
1 

2 
1 


2
The two photons are
now correlated, even
though they never
interacted!
Explanation involves destructive
1  1  1  1 



0
interference of amplitudes:
2
2
2 2
Final amplitude of non-collision is
Getting Formal
The basis states have the form |S=|s1,…,sm, where
si is the number of photons in the ith “mode”
We’ll never create or destroy photons. So s1+…+sm=n
is constant.
For us, m=poly(n)
Initial state:
|I=|1,…,1,0,……,0 
U
You get to apply any mm unitary matrix U
If n=1 (i.e., there’s only one photon, in a superposition over the m
modes), U acts on that photon in the obvious way
 m  n  1

M : 
n 

In general, there are
ways to
distribute n identical photons into m modes
U induces an MM unitary (U) on the n-photon
states as follows:
Per U
 U S ,T 

S ,T

s1! sm !t1! t m !
Here US,T is an nn submatrix of U (possibly with repeated
rows and columns), obtained by taking si copies of the ith
row of U and tj copies of the jth column for all i,j
Beautiful Alternate Perspective
The “state” of our computer, at any time, is a degree-n
polynomial over the variables x=(x1,…,xm) (n<<m)
Initial state: p(x) := x1xn
We can apply any mm unitary transformation U to x,
to obtain a new degree-n polynomial
p' x   pUx 
 x



S  s1 ,, sm
s1
S 1
sm
m
x
s1
1
Then on “measuring,” we see the monomial x  x
2
with probability
 S s1! sm !
sm
m
OK, so why is it hard to sample the
distribution over photon numbers classically?
Given any matrix ACnn, we can construct an mm
unitary U (where m2n) as follows:
 A B 

U  
 C D
Suppose we start with |I=|1,…,1,0,…,0 (one photon
in each of the first n modes), apply U, and measure.
Then the probability of observing |I again is
p : I  U  I
2

2n
Per  A
2
Claim 1: p is #P-complete to
estimate (up to a constant factor)
Idea: Valiant proved that the
PERMANENT is #P-complete.
Can use a classical reduction
to go from a multiplicative
approximation of |Per(A)|2
to Per(A) itself.
 
Claim 2: Suppose we had a
fast classical algorithm for
boson sampling. Then we
could estimate p in BPPNP
Idea: Let M be our classical
sampling algorithm, and let r
be its randomness. Use
approximate counting to
estimate Pr M r  outputs I
2
r

 
Conclusion:
p : Suppose
I  U weI had a fast
 classical
Per Aalgorithm
for boson sampling. Then P#P=BPPNP.
2n
2

The Elephant in the Room
The previous result hinged on the difficulty of
estimating a single, exponentially-small probability
p—but what about noise and error?
The “right” question: can a classical computer
efficiently sample a distribution with 1/poly(n)
variation distance from the boson distribution?
Our Main Result: Suppose it can. Then there’s a BPPNP
algorithm to estimate |Per(A)|2, with high probability
nn
over a Gaussian matrix
 C
A ~ N 0 ,1
Our Main Conjecture
Estimating |Per(A)|2, for most Gaussian
matrices A, is a #P-hard problem
If the conjecture holds, then even a noisy n-photon
experiment could falsify the Extended Church Thesis,
assuming P#PBPPNP!
Most of our paper is devoted to giving evidence for
this conjecture
We can prove it if you replace “estimating” by
“calculating,” or “most” by “all”
First step: understand the distribution
of |Per(A)|2 for random A
Conjecture:
There exist constants C,D and >0 such that for all n and >0,
Pr
X ~ N 0,1Cnn
PerX    n! Cn 
D

Empirically true!
Also, we can prove it with
determinant in place of
permanent
The Equivalence of
Sampling and Searching
[A., CSR 2011]
[A.-Arkhipov] gave a “sampling problem” solvable using
quantum optics that seems hard classically—but does
that imply anything about more traditional problems?
Recently, I found a way to convert any sampling
problem into a search problem of “equivalent difficulty”
Basic Idea: Given a distribution D, the search problem is
to find a string x in the support of D with large
Kolmogorov complexity
Using Quantum Optics to Prove
that the Permanent is #P-Hard
[A., Proc. Roy. Soc. 2011]
Valiant famously showed that the permanent is #P-hard—
but his proof required strange, custom-made gadgets
We gave a new, more transparent proof by combining
three facts:
(1) n-photon amplitudes correspond to nn permanents
(2) Postselected quantum optics can simulate universal
quantum computation [Knill-Laflamme-Milburn 2001]
(3) Quantum computations can encode #P-hard quantities
in their amplitudes
Experimental Issues
Basically, we’re asking for the n-photon generalization
of the Hong-Ou-Mandel dip, where n = big as possible
Our results suggest that such a generalized HOM dip would
be evidence against the Extended Church-Turing Thesis
Physicists: “Sounds hard! But not as hard as full QC”
Remark: If n is too large, a classical computer couldn’t
even verify the answers! Not a problem yet though…
Several experimental groups (Imperial College, U. of
Queensland) are currently working to do our
experiment with 3 photons. Largest challenge they
face: reliable single-photon sources
Summary
Thinking about quantum optics led to:
- A new experimental quantum computing proposal
- New evidence that QCs are hard to simulate
classically
- A new classical randomized algorithm for
estimating permanents
- A new proof of Valiant’s result that the permanent
is #P-hard
- (Indirectly) A new connection between sampling
and searching
Open Problems
Prove our main conjecture: that Per(A) is #P-hard to
approximate for a matrix A of i.i.d. Gaussians ($1,000)!
Can our model solve classically-intractable decision
problems?
Fault-tolerance in the quantum optics model?
Find more ways for quantum complexity theory to “meet
the experimentalists halfway”
Bremner, Jozsa, Shepherd 2011: QC with commuting
Hamiltonians can sample hard distributions