Download Goal: To understand Electro-magnetic fields

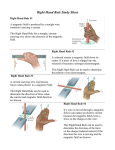
Goal: To understand Electromagnetic fields
Objectives:
1) Learn what Electro-Magnetic Fields are
2) Learn how to calculate the Magnetic Force on a
wire
3) Learn to find the Magnetic Field for a straight
wire
4) Learn to calculate the Magnetic Field from a
coiled wire
5) To learn about Solenoids
6) Learn how to create your own magnet!
Electro-Magnetic Fields
• Magnetic Fields tend to occur in the
presence of electric fields when there are
moving charges.
• In fact Magnetic Fields are created to
offset the electric field and the moving
charges!
• Conversely a magnetic field can induce an
electric current – but that is tomorrow.
Magnetic Force on a wire
• If a wire is in a magnetic field then there
will be a force exerted on it!
• F = q VXB
• But, I = q / t
• So, qV =q L / t = I * L
• So, F = I L X B
Direction of the force
• But what about the direction the force?
• The current is moving up or down the wire.
• For a wire, the magnetic field circles the wire in a
direction counter clockwise to the direction of the
current.
• One way to remember this is to use you hand –
and your thumb is the current.
• The field is your closed hand (give the magnetic
field a thumbs up!)
• The force is in the direction of LXB
• So, it will always be towards or away from the
wire.
Magnetic Fields from a wire
• A wire with charge will create a magnetic field!
• As you get further from the wire this field will do
down.
• However, the amount of the wire that affects you
increases a little (so you get over distance
instead of distance squared).
• B = μ0 I / (2π r)
• Where μ0 = 4 π * 10-7 Tm/A (permeability of free
space)
2 Wire example
• Suppose we have 2 parallel wires leading in
the +x direction.
• The current through both wires is 3 A.
• They are separated by a distance of 0.1 m.
• What is the magnitude and direction of the
magnetic field exerted on the top wire by
the bottom wire?
2 Wire example
• Suppose we have 2 parallel wires leading in the
+x direction.
• The current through both wires is 3 A.
• They are separated by a distance of 0.1 m.
• What is the magnitude and direction of the
magnetic field exerted on the top wire by the
bottom wire?
• B = μ0 I / (2π r)
• B = 4 π * 10-7 Tm/A * 3A / (2π 0.1m)
• B = 6 * 10-6 T and from right hand rule in the +z
direction
2 Wire example - force
• Suppose we have 2 parallel wires leading in the +x
direction.
• The current through both wires is 3 A.
• They are separated by a distance of 0.1 m.
• B = 6 * 10-6 T and from right hand rule in the +z direction
• What is the magnitude and direction of the magnetic
force exerted on the top wire by the bottom wire for a 1m
segment of the wire?
• Note: in HW they will so F/L for this and give you some
value in N/m for F/L.
2 Wire example - force
• Suppose we have 2 parallel wires leading in the +x
direction.
• The current through both wires is 3 A.
• They are separated by a distance of 0.1 m.
• B = 6 * 10-6 T and from right hand rule in the +z direction
• What is the magnitude and direction of the magnetic
force exerted on the top wire by the bottom wire for a 1m
segment of the wire?
• F = I LXB = 3A * 1m * 6 * 10-6 T = 1.8 * 10-5 N
• Direction? Well L is in the +X direction and B is in the +Z
direction.
• Right hand rule…
• F is in the –y direction (down)
Magnetic field from a circular
current loop
• This one is the opposite of the straight wire in
terms of finding direction.
• The loop makes a plane.
• The magnetic field will be perpendicular to that
plane.
• Use your right hand.
• Your curled fingers are the current.
• Note it is counterclockwise.
• Your thumb in this case is the magnetic field.
Magnetic field equation
• Lets suppose you have N loops (N can
equal 1).
• Inside the loop:
B = μ0 N I / (2 r)
• And here r is the radius of the loop not the
distance from the loop.
Solenoids
• You can add a lot of loops over some
extended length and get a solenoid.
• MRI machines are solenoids.
• Inside the solenoid B = μ0 N I / (L)
• L here is the length of the solenoid.
• Notice that it does not depend on the
radius of the solenoid.
• Also, N/L = n (n is often quoted in the
homework).
Build a Magnet!
•
•
•
•
Tired of loosing those screws?
Magnetize your screwdriver!
But how?
Well, just wrap a wire around the screwdriver,
then connect both ends of the wire to a power
supply (such as a battery, but not too powerful or
you might hurt yourself).
• Leave it on for some time, few minutes, and
when you turn it off you will have yourself a
magnetized screwdriver!
• No more dropping screws into your computer’s
power supply…
Conclusion
• We have learned how to find electromagnetic
forces.
• We have examined the magnetic fields from
straight and looped wires as well as solenoids.
• We learned how to use the Right Hand Rule to
find the direction the current and magnetic fields
for wires.
• We have seen how to find the force exerted on
wires.
• We have discovered how to build our own
magnets!