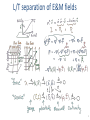* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Fundamental nuclear symmetries meet classical electrodynamic
Electricity wikipedia , lookup
Abraham–Minkowski controversy wikipedia , lookup
Magnetic monopole wikipedia , lookup
Superconductivity wikipedia , lookup
Nanofluidic circuitry wikipedia , lookup
Electrostatics wikipedia , lookup
Waveguide (electromagnetism) wikipedia , lookup
Multiferroics wikipedia , lookup
Electromotive force wikipedia , lookup
Eddy current wikipedia , lookup
Electromagnetic radiation wikipedia , lookup
Magnetohydrodynamics wikipedia , lookup
Faraday paradox wikipedia , lookup
Lorentz force wikipedia , lookup
Maxwell's equations wikipedia , lookup
Electromagnetism wikipedia , lookup
Mathematical descriptions of the electromagnetic field wikipedia , lookup
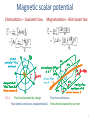
PHY 417G: Review Christopher Crawford 2015-04-29 Classical Electromagnetic Field • action at a distance vs. locality • field ”mediates “carries force • extends to quantum field theories • field is everywhere always E (x, t) • differentiable, integrable • field lines, equipotentials • PDE – boundary value problems • solution to physical problems 2 Boundary Value Problem (BVP) • Partial Differential Equation (PDE) BULK – Represents the physics of continuous media – General solution by separation of variables – Linear equation –> inf. dim. linear solution function space • Boundary Conditions (BC) SURFACE Use orthogonality to calculate components of gen. solution Interior BCs – continuity – Derives directly from the PDE Exterior BCs – physics input – Uniqueness theorem: one BC per surface (elliptic) 1 or 2 initial conditions (diffusion, hyperbolic wave) • Now we just have to know the PDE to solve! 3 Magnetic scalar potential Electrostatics – Coulomb’s law B.C.’s: Magnetostatics – Biot-Savart law Flux lines bounded by charge Flow sheets continuous (equipotentials) Flux lines continuous Flow sheets bounded by current 4 L/T separation of E&M fields 5 Formulations of E & M PDEs • Electricity Magnetism • Note the interchange of flux and flow: twisted symmetry! 6 Electrodynamics • Faraday’s law: 3rd experimental law – – – – Motional EMF equivalent to truly moving or changing magnetic field Basis of special relativity – electromagnetic field F = E dt + B 3 “Ampère’s Laws”: H(J), A(B), E(eB/dt) 3+1 lumped components: capacitor, resistor, inductor (reluctance) • Maxwell’s displacements current: theoretical prediction – – – – Relativistic complete derivative chain: gauge, potential, fields, current Completes Maxwell equations – PDE’s of electrodynamics Macroscopic equations: 3 charges + 5 currents We could go back and create 5 formulations of electrodynamics: • I) Jefimenko’s eqs, II+III) Maxwell’s integral/differential equations IV) Retarded potential: Green’s function of V) WAVE EQUATION 7 Polarization & Magnetization • Chapter 4: electric materials –> Chapter 6: magnetic materials • Polarization chain –> Magnetization mesh 8 3 Materials –> 3 Components • Materials constants: permittivity, resistivity, permeability • Electrical components: capacitor, resistor, inductor • Each is a ratio of Flux / Flow ! 9 Equations of Electrodynamics 10 Dynamics of E&M • Maxwell’s equations – dynamics of the field – Source equations – charge (ρ,J) generates the E&M field – Force equations – nature of E&M force: conservation of (E,p) • Lorentz Force equation – dynamics of charged particles – Additional equation independent of Maxwell eq’s. – Integrate to get energy E=Fdx, momentum p=Fdt, • Conserved currents – Charge (current density) – Energy (Poynting vector) – Momentum (stress tensor) • Conservation principles can be used to simplify problems 11 Electromagnetic waves • Homogeneous wave equation – Helmholtz equation – Separation of variables / eigenfunctions: Exp, Legendre, Bessel – 3 material properties (ε, μ, σ) –> 2 complex medium properties • Dispersion relation k(ω): propagation (attenuation, wavelength) • Characteristic Impedance Z(ω): boundary (reflection, phase shift) • Boundary value problems – Across an interface: Fresnel coefficients reflection / transmission [impedance] – Along a wave guide: modes of propagation standing transverse waves, kt2 affects dispersion relation • Examples of waves – 1-d: String wave, – 2-d: Surface waves, gravity waves, – 3-d: Seismic/acoustic waves, telegrapher’s equations transverse waveguide modes electromagnetic waves 12 Final exam: • Integration – Biot-Savart, vector potential – Ampère’s law H(J), Potential A(B), Faraday’s law E(dB/dt) – Calculation of Resistance, Inductance, Reluctance • Dynamics and Conservation – Derivation of magnetic formulations, potentials, wave equations – Derivation of conservation principles: charge, energy, momentum • Boundary value problems – Magnetostatic with materials – Interface reflection/transmission – Waveguide modes • Essay questions – long and short – Flux, flow, Maxwell equations, displacement currents, waves – Properties of materials: magnetization, dispersion, impedance 13