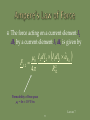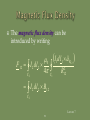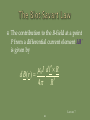Download magnetic dipole

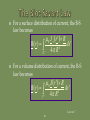
Lecture 7: Magnetostatics: Ampere’s
Law Of Force; Magnetic Flux
Density; Lorentz Force; Biot-savart
Law; Applications Of Ampere’s Law
In Integral Form; Vector Magnetic
Potential; Magnetic Dipole;
Magnetic Flux
Lecture 7
1






To begin our study of magnetostatics
with Ampere’s law of force;
magnetic flux density; Lorentz force;
Biot-Savart law;
applications of Ampere’s law in integral
form; vector magnetic potential;
magnetic dipole;
magnetic flux.
Lecture 7
2
Fundamental laws of
classical electromagnetics
Special
cases
Electrostatics
Statics:
Input from
other
disciplines
Maxwell’s
equations
Magnetostatics
Electromagnetic
waves

0
t
Geometric
Optics
Transmission
Line
Theory
Circuit
Theory
Kirchoff’s
Laws
d  
Lecture 7
3



Magnetostatics is the branch of
electromagnetics dealing with the effects of
electric charges in steady motion (i.e, steady
current or DC).
The fundamental law of magnetostatics is
Ampere’s law of force.
Ampere’s law of force is analogous to
Coulomb’s law in electrostatics.
Lecture 7
4

In magnetostatics, the magnetic field is
produced by steady currents. The
magnetostatic field does not allow for
 inductive coupling between circuits
 coupling between electric and magnetic
fields
Lecture 7
5



Ampere’s law of force is the “law of action”
between current carrying circuits.
Ampere’s law of force gives the magnetic
force between two current carrying circuits
in an otherwise empty universe.
Ampere’s law of force involves complete
circuits since current must flow in closed
loops.
Lecture 7
6

Experimental facts:


Two parallel wires
carrying current in
the same direction
attract.
Two parallel wires
carrying current in
the opposite
directions repel.
F21 F12

I1
F21

I2
F12

I1

I2
Lecture 7
7

Experimental facts:

A short currentcarrying wire
oriented
perpendicular to a
long currentcarrying wire
experiences no
force.
F12 = 0

I2
I1
Lecture 7
8

Experimental facts:
 The magnitude of the force is inversely
proportional to the distance squared.
 The magnitude of the force is
proportional to the product of the
currents carried by the two wires.
Lecture 7
9

The direction of the force established
by the experimental facts can be
mathematically represented by
unit vector in direction
of current I2

unit vector in direction
of current I1
aˆ F1 2  aˆ 2  aˆ1  aˆ R1 2
unit vector in
direction of force on
I2 due to I1

unit vector in direction
of I2 from I1
Lecture 7
10

The force acting on a current element I2
dl2 by a current element I1 dl1 is given by
 0 I 2 d l 2  I1d l 1  aˆ R
F 12 
2
4
R12
12

Permeability of free space
0 = 4  10-7 F/m
Lecture 7
11

The total force acting on a circuit C2
having a current I2 by a circuit C1 having
current I1 is given by
 0 I1 I 2
F 12 
4

C 2 C1

d l 2  d l 1  aˆ R1 2

2
12
R
Lecture 7
12

The force on C1 due to C2 is equal in magnitude
but opposite in direction to the force on C2 due
to C1.
F 21   F 12
Lecture 7
13



Ampere’s force law describes an “action
at a distance” analogous to Coulomb’s
law.
In Coulomb’s law, it was useful to
introduce the concept of an electric field
to describe the interaction between the
charges.
In Ampere’s law, we can define an
appropriate field that may be regarded as
the means by which currents exert force
Lecture 7
on each other.
14

The magnetic flux density can be
introduced by writing
0
F 12   I 2 d l 2 
4
C
2

C1
I d l
1
1
 aˆ R1 2

2
12
R
  I 2 d l 2  B12
C2
Lecture 7
15

where
0
B12 
4

I1d l 1  aˆ R1 2
C1
2
12
R
the magnetic flux density at the location of
dl2 due to the current I1 in C1
Lecture 7
16

Suppose that an infinitesimal current
element Idl is immersed in a region of
magnetic flux density B. The current
element experiences a force dF given by
d F  Id l  B
Lecture 7
17

The total force exerted on a circuit C
carrying current I that is immersed in a
magnetic flux density B is given by
F  I  dl  B
C
Lecture 7
18

A moving point charge placed in a
magnetic field experiences a force
given
F byQ v  B
Id l  Q v
m
Q
v
B
The force experienced
by the point charge is
in the direction into the
paper.
Lecture 7
19

If a point charge is moving in a region
where both electric and magnetic fields
exist, then it experiences a total force given
by
F  F e  F m  q E  v  B 

The Lorentz force equation is useful for
determining the equation of motion for
electrons in electromagnetic deflection
Lecture 7
systems such as CRTs.
20


The Biot-Savart law gives us the B-field arising
at a specified point P from a given current
distribution.
It is a fundamental law of magnetostatics.
Lecture 7
21

The contribution to the B-field at a point
P from a differential current element Idl’
is given by
0 I d l  R
d B (r ) 
3
4 R
Lecture 7
22
P
R
Id l 
r
r
Lecture 7
23

The total magnetic flux at the point P due
to the entire circuit C is given by
0 I d l  R
B (r )  
3
4 R
C
Lecture 7
24



Line current density (current) - occurs
for infinitesimally thin filamentary
bodies (i.e., wires of negligible
diameter).
Surface current density (current per unit
width) - occurs when body is perfectly
conducting.
Volume current density (current per unit
cross sectional area) - most general.
Lecture 7
25

For a surface distribution of current, the B-S
law becomes
 0 J s r   R
B (r )  
ds 
3
4 R
S

For a volume distribution of current, the B-S
law becomes
 0 J r   R
B (r )  
dv 
3
4 R
V
Lecture 7
26

Ampere’s Circuital Law in integral form
states that “the circulation of the
magnetic flux density in free space is
proportional to the total current
through the surface bounding the path
over which the circulation is
computed.”
B

d
l


I
0
encl

C
Lecture 7
27
By convention, dS is
taken to be in the
direction defined by the
right-hand rule applied
to dl.
dl
dS
S
I encl   J  d s
S
Since volume current
density is the most
general, we can write
Iencl in this way.
Lecture 7
28


Just as Gauss’s law follows from
Coulomb’s law, so Ampere’s circuital
law follows from Ampere’s force law.
Just as Gauss’s law can be used to derive
the electrostatic field from symmetric
charge distributions, so Ampere’s law
can be used to derive the magnetostatic
field from symmetric current
distributions.
Lecture 7
29

Ampere’s law in integral form is an
integral equation for the unknown
magnetic flux density resulting from a
given current distribution.
B

d
l


I
0
encl

C
known
unknown
Lecture 7
30


In general, solutions to integral equations
must be obtained using numerical
techniques.
However, for certain symmetric current
distributions closed form solutions to
Ampere’s law can be obtained.
Lecture 7
31


Closed form solution to Ampere’s law
relies on our ability to construct a
suitable family of Amperian paths.
An Amperian path is a closed contour to
which the magnetic flux density is
tangential and over which equal to a
constant value.
Lecture 7
32
Consider an infinite line current along the
z-axis carrying current in the +zdirection:
I
Lecture 7
33
(1) Assume from symmetry and the righthand rule the form of the field
B  aˆ B   
(2) Construct a family of Amperian paths
circles of radius  where
Lecture 7
34
(3) Evaluate the total current passing
through the surface bounded by the
Amperian path
I encl   J  d s
S
Lecture 7
35
y
Amperian path

x
I
I encl  I
Lecture 7
36
(4) For each Amperian path, evaluate the
integral
length
B

d
l

Bl

C
magnitude of B
on Amperian
path.
of Amperian
path.
 B  d l  B   2 
C
Lecture 7
37
(5) Solve for B on each Amperian path
 0 I encl
B
l
0 I
B  aˆ
2 
Lecture 7
38
 B dl    Bd s
C
S
  0 I encl   0  J  d s
S
 Because the above must hold for any
surface S, we must have
Differential form
of Ampere’s Law
  B  0 J
Lecture 7
39

Ampere’s law in differential form implies
that the B-field is conservative outside of
regions where current is flowing.
Lecture 7
40

Ampere’s law in differential form
  B  0 J

No isolated magnetic charges
B  0
B is solenoidal
Lecture 7
41

Vector identity: “the divergence of the
curl of any vector field is identically
zero.”
    A   0

Corollary: “If the divergence of a vector
field is identically zero, then that vector
field can be written as the curl of some
vector potential field.”
Lecture 7
42

Since the magnetic flux density is
solenoidal, it can be written as the curl of
a vector field called the vector magnetic
potential.
B  0

B   A
Lecture 7
43

The general form of the B-S law is
 0 J r   R
B (r )  
dv 
3
4 R
V

Note that
R
1
    3
R
R
Lecture 7
44

Furthermore, note that the del operator
operates only on the unprimed
coordinates so that
J r  R
1

  J r   
3
R
R
1
    J r 
R
 J r  
 

 R 
Lecture 7
45

Hence, we have
0
B r    
4
J r 

d
v
V  R
Ar 
Lecture 7
46

For a surface distribution of current, the
vector magnetic potential is given by
0
A( r ) 
4

J s r 
S  R ds
For a line current, the vector magnetic
potential is given by
0 I d l
A( r ) 

4 L R
Lecture 7
47


In some cases, it is easier to evaluate the
vector magnetic potential and then use
B =  A, rather than to use the B-S law
to directly find B.
In some ways, the vector magnetic
potential A is analogous to the scalar
electric potential V.
Lecture 7
48


In classical physics, the vector magnetic
potential is viewed as an auxiliary
function with no physical meaning.
However, there are phenomena in
quantum mechanics that suggest that the
vector magnetic potential is a real (i.e.,
measurable) field.
Lecture 7
49


A magnetic dipole comprises a small
current carrying loop.
The point charge (charge monopole) is
the simplest source of electrostatic
field. The magnetic dipole is the
simplest source of magnetostatic field.
There is no such thing as a magnetic
monopole (at least as far as classical
physics is concerned).
Lecture 7
50


The magnetic dipole is analogous to the
electric dipole.
Just as the electric dipole is useful in
helping us to understand the behavior of
dielectric materials, so the magnetic
dipole is useful in helping us to
understand the behavior of magnetic
materials.
Lecture 7
51

Consider a small circular loop of radius b
carrying a steady current I. Assume that
the wire radius has a negligible crosssection.
y
x
b
Lecture 7
52

The vector magnetic potential is
evaluated for R >> b as
 0 I 2 aˆ bd 
A(r ) 
R
4 0
 0 Ib 2
 1 b sin  cos    

d 
 aˆ x sin    aˆ y cos   

2


r
4 0

r
 0 Ib
b sin 

 aˆ x sin   aˆ y cos  

r2
4
 0 Ib 2
sin 
 aˆ
2
4 r
Lecture 7
53

The magnetic flux density is evaluated for R
>> b as
0
2
ˆ
ˆ



B   A 
I

b
a
2
cos


a
r
 sin  
3
4 r
Lecture 7
54

Recall electric dipole
p
aˆ r 2 cos   aˆ sin  
E
3
4 0 r
p  electric dipole moment  Qd

The electric field due to the electric
charge dipole and the magnetic field
due to the magnetic dipole are dual
quantities.
Lecture 7
55

The magnetic dipole moment can be
defined as
2
m  aˆ z I b
Direction of the dipole moment
is determined by the direction
of current using the right-hand
rule.
Magnitude of
the dipole
moment is the
product of the
current and
the area of the
loop.
Lecture 7
56


We can write the vector magnetic
potential in terms of the magnetic
dipole moment as
 0 m sin   0 m  aˆ r
A  aˆ

2
2
4 r
4 r
We can write the B field in terms of the
magnetic dipole moment as
0
0 
 1 
B
m aˆ r 2 cos   aˆ sin   
 m   
3
4 r
4 
 r 
Lecture 7
57

The B-field is solenoidal, i.e. the divergence of
the B-field is identically equal to zero:
B  0


Physically, this means that magnetic charges
(monopoles) do not exist.
A magnetic charge can be viewed as an isolated
magnetic pole.
Lecture 7
58


No matter how
small the
magnetic is
divided, it always
has a north pole
and a south pole.
The elementary
source of
magnetic field is a
magnetic dipole.
N
N
S
S
N
S
N
I
S
Lecture 7
59

The magnetic flux
crossing an open
surface S is given
by
B
   Bds
Wb
S
C
S
Wb/m2
Lecture 7
60

From the divergence theorem, we have
  B  0     B dv  0   B  d s  0
V

S
Hence, the net magnetic flux leaving any
closed surface is zero. This is another
manifestation of the fact that there are no
magnetic charges.
Lecture 7
61

The magnetic flux across an open
surface may be evaluated in terms of
the vector magnetic potential using
Stokes’s theorem:
   B d s    A d s
S
S
  Adl
C
Lecture 7
62