Download Capability-Based Optimization in Mediators

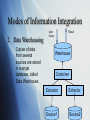
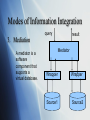
Capability-Based Optimization in
Mediators
Rohit Deshmukh
ID 120
CS-257
Modes of Information Integration
1. Federated Collection
Sources are
Independent, but
one source can call
on others to supply
Information
DB1
DB2
DB3
DB4
Modes of Information Integration
2. Data Warehousing
Copies of data
from several
sources are stored
in a single
database, called
Data Warehouse.
User
Query
Result
Warehouse
Combiner
Extractor
Extractor
Source1
Source2
Modes of Information Integration
query
result
3. Mediation
A mediator is a
software
component that
supports a
virtual database.
Mediator
Wrapper
Wrapper
Source1
Source2
Capability-Based Optimization in
Mediators
Problem of Limited Source Capabilities
 Many useful sources have only Web-based interfaces
 Web sources usually permit querying only through a query
form
 Legacy systems(designed to be queried in specific way)
 Reasons of security
 Indexes on large databases may make certain kinds of queries
feasible while others too expensive
Capability-Based Optimization in
Mediators
Notation for Describing Source Capabilities
 f (free) The attribute can be specified or not.
 b(bound) We must specify a value for the attribute, any
value is allowed.
 u(unspecified) we are not permitted to specify value for the
attribute
 c[S] choice from set S
 o[S] optional from set S
 We place a prime e.g. b’ on a code if the attribute
is not a part of the output query.
Notation for Describing Source
Capabilities

Example Dealer 1 is a source of data in the form
Cars(SerialNo, model, color, autoTrans,
cdPlayer)
Two possible ways that Dealer 1 might allow to be queried
1. b’uuuu
2. ubbo[yes,no]o[yes,no]
•
Alternative adornment, suppose that queries limit the
model and color attributes to valid values;
uc[modelx,gobi,…]c[red,blue,….]o[yes,no]o[yes,no]
f(free); b(bound); u(unspecified); c[S] ; o[S]
Capability-Based Query-Plan
Selection


A capability based query optimizer first
considers what queries it can ask at the sources
that will help answer the query.
The bindings may make some more queries at
the sources.The process is repeated until
 We have asked enough queries at the sources to
resolve all the conditions of the mediator
queries.Such a plan is called feasible.
 We can construct no more valid forms of source
queries. In which case the mediator must give up.
Capability-Based Query-Plan
Selection
 Example Dealer 2 has two different sources.
1. Autos(serial, model, color)
2. Options(serial, option)
Assuming we have only the following
adornments for the two sources.
• ubf for Autos
• bu and uc [autoTrans, cdPlayer].
f(free); b(bound); u(unspecified); c[S] ; o[S]
Example

Find the serial numbers and colors of Modelx
with a CD player.
1. Select (serial,color) from Autos where
model=modelx
2. Use bu for Options source
for each serial from above match;
option = CdPlayer
f(free); b(bound); u(unspecified); c[S] ; o[S]
Example

1.
2.
3.
Find the serial numbers and colors of Modelx with a CD
player.
Query Options
Select serial from options
where option = CdPlayer
Now query Autos
Select (serial,colors) where
model = modelx;
Intersect the two sets of serial numbers.
f(free); b(bound); u(unspecified); c[S] ; o[S]
Example

1.
2.

Find the serial numbers and colors of Modelx with a CD
player.
Query Options as in previous case
Select serial from options
where option = CdPlayer
Use these serial numbers to query Autos,
select color where
serial = (selected serial) and model = modelx
This would not work because the second part, does not
have a matching adornment.
A Capability-based optimizer eliminates infeasible plans
such as this one.
f(free); b(bound); u(unspecified); c[S] ; o[S]