Download introduction

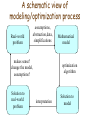
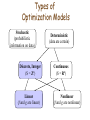
Math443/543
Mathematical Modeling and
Optimization
A schematic view of
modeling/optimization process
Real-world
problem
assumptions,
abstraction,data,
simplifications
makes sense?
change the model,
assumptions?
Solution to
real-world
problem
Mathematical
model
optimization
algorithm
interpretation
Solution to
model
What is a model?
• Model: A schematic description
of a system, theory, or phenomenon that
accounts for its known or inferred properties
and maybe used for further study of its characteristics.
• Mathematical models
– are abstract models
– describe the mathematical relationships
among elements in a system
• In this class, mathematical models dealing
with discrete optimization
Mathematical models in
Optimization
• The general form of an optimization model:
min or max f(x1,…,xn)
(objective function)
subject to gi(x1,…,xn) ≥ 0
(functional constraints)
x1,…,xn  S
(set constraints)
• x1,…,xn are called decision variables
• In words,
the goal is to find x1,…,xn that
– satisfy the constraints;
– achieve min (max) objective function value.
Types of
Optimization Models
Stochastic
(probabilistic
information on data)
Discrete, Integer
(S = Zn)
Linear
(f and g are linear)
Deterministic
(data are certain)
Continuous
(S = Rn)
Nonlinear
(f and g are nonlinear)
What is Discrete Optimization?
Discrete Optimization
is a field of applied mathematics,
combining techniques from
• combinatorics and graph theory,
• linear programming,
• theory of algorithms,
to solve optimization problems
over discrete structures.
Examples of Discrete Optimization
Models: Traveling Salesman Problem
(TSP)
There are n cities. The salesman
 starts his tour from City 1,
 visits each of the cities exactly once,
 and returns to City 1.
For each pair of cities i,j there is a cost cij
associated with traveling from City i to City j .
Goal: Find a minimum-cost tour.
Examples of Discrete Optimization
Models: Job Scheduling
 There are 4 jobs that should be processed on the same
machine. (Can’t be processed simultaneously).
Job k has processing time pk .
Here is an example of a possible schedule:
Job 3
0
Job 1
2
Job 4
6
Job 2
9
 Goal: Find a schedule which minimizes
the average completion time of the jobs.
14
time
Examples of Discrete Optimization
Models: Shortest Path Problem
 In a network, we have distances on arcs ;
source node s and sink node t .
3
a
1
1
1
2
s
d
4
7
c
2
t
2
1
b
4
5
2
e
 Goal: Find a shortest path from the source to the sink.
Problems that can be modeled
and solved by discrete
optimization techniques
•
•
•
•
•
Scheduling Problems (production, airline, etc.)
Network Design Problems
Facility Location Problems
Inventory management
Transportation Problems
Problems that can be modeled
and solved by discrete
optimization techniques
•
•
•
•
•
Minimum spanning tree problem
Shortest path problem
Maximum flow problem
Min-cost flow problem
Assignment Problem
Solution Methods for Discrete
Optimization Problems
•
•
•
•
Integer Programming
Network Algorithms
Dynamic Programming
Approximation Algorithms