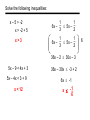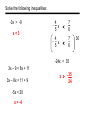Download x < 3

Math 010
Unit 6
Lesson 4
Objectives:
• to write a set in roster notation
• to write a set in set-builder notation
• to graph an inequality on the number line
Sets - the roster method
The roster method of writing a set encloses a
list of the elements in braces.
Examples:
1. The set of the last three letters in
the alphabet.
{x, y, z}
2. The set of integers between 0 and 10
{1, 2, 3, 4, 5, 6, 7, 8, 9}
3. The set of integers greater than or
equal to 4
{4, 5, 6, . . .}
Other definitions
The empty set is the set that contains no elements
The symbol for the empty set is { } or 
The union of two sets, written A  B is the set
that contains the elements of A and the elements
of B
The intersection of two sets, written A  B is
the set that contains the elements that are
common to both A and B
A = {3, 5, 7, 9, 11}
AB =
B = { 4, 6, 8, 10, 12}
{3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
B  C = {8, 10}
AC = 
C = {2, 8, 10, 14}
Another method of representing sets is called set-builder
notation.
{x|x < 10, x positive integers}
The set of all x such that x is less than 10 and x is an
element of the positive integers.
Read the following set:
{x| x > 5, x integers}
The set of all x such that x is greater than 5 and x is an
element of the integers.
Write the following in set builder notation
The set of negative integers greater than -100
{x | x > -100, x  negative integers}
The set of real numbers less than 3
{x | x < 3 , x  real numbers}
Graph the inequality:
{x | x > 1, x  real numbers}
(
-10
-5
0
5
10
The parentheses indicate that 1 is not included in the graph.
A bracket, [ , would indicate that a number is included in the
graph.
Another method of graphing the same inequality is shown below.
-10
-5
0
5
10
Graph the following: {x | x  2}
-10
-5
0
5
10
Graph the following: {x | x  -1}  {x | x > 2}
-10
-5
0
5
Remember: The union of two graphs are the points that are in
one graph or the other.
10
Graph the following: {x | x < 5}  {x | x > -1}
-10
-5
0
5
Remember:
The intersection of the two graphs is the set of points they
have in common
10
Solving
and
Graphing
Inequalities
Linear inequalities are solved like linear equations
•
with one exception
Simplify
Collect
Divide
each side of the inequality
terms
by the coefficient of the variable
• switch the inequality sign if dividing or multiplying both
sides of the inequality by a negative number
Solve the following inequalities:
x – 5 > -2
x > -2 + 5
1
1
6x –
 5x –
3
2
x>3
1
1
6x –
 5x –
3
2
36x – 2  30x – 3
5x – 9 < 4x + 3
5x – 4x < 3 + 9
x < 12
36x – 30x  -3 + 2
6x  -1
x  -1
6
6
Solve the following inequalities:
-3x > -9
x<3
- 4 x
5
- 4 x
5
<
7
6
<
7
6
-24x < 35
3x – 9 < 8x + 11
3x – 8x < 11 + 9
-5x < 20
x > -4
x > - 35
24
30
Words and Symbols
at least
at most


A basketball team must win at least 60% of their
remaining games to qualify for the playoffs. They
have 17 games left. How many must they win?
Let x = games
they must win
x  .6(17)
x  10.2
The team must win at least 11 games
Solve the inequality and graph the solution
-8x > 8
x < -1
)
-10
-5
0
5
10
0
5
10
or
-10
-5