Download Frequency response of CE amplifier

FREQUENCY RESPONSE OF THE
SINGLE STAGE BJT AMPLIFIER IN CE CONFIGURATION
I.OBJECTIVES
a) Learning the experimental method to find the frequency response.
b) The determination of the 3dB bandwidth.
c) The determination of the effects of the capacitive elements and of the gain on the bandwidth
II. COMPONENTS AND INSTRUMENTATION
We will work with the experimental assembly from Fig. II.3.7. For supply a dc voltage source will be used.
The sine wave signals are applied from a signal generator and are visualized with a dual channel
oscilloscope. In order to measure the dc voltages we will use a dc voltmeter.
III. PREPARATION
P1. The frequency response
The equivalent circuit of showing the connection between the signal source vs with the internal
resistance Rs and the amplifier is presented in Fig. II.3.1.
Rs
vs
Cc
Ri
Ci
Fig. II 3.1. The equivalent circuit
Ri and Ci are the resistance, respective the input capacity of the amplifier.
We analyse the circuit in three frequency domains: low, medium and high.
 The values fL and fH, for the circuit from the figure Fig II.3.6, are deduced by replacing the transistor
with its model at high and low frequencies and by writing the complex transfer function of the circuit.
 At low frequencies, the equivalent capacity Cech between the base and the emitter is considered a
discontinuity (very low capacity  pF), resulting the equivalent circuit from the figure Fig.II.3.2 :
1
iS
iB
ZS
iC
iO
ZO
VBE
rBE
RC
RB
VS
RL
gmVBE
i1
(β+1)iB
VO1
ZE
iO
VO
RB =
R1R2
R1+R2
Fig. II.3.2. The small signal model of the BJT at low frequencies
where:
ZS =
1+jωCCRS
jωCC
ZE=
RE
1+jωCERE
ZO =
1
jωCO
After the computations on the small signal model of the BJT at low frequencies, the following expresion of
the transfer function was obtained :
H(jω)=
If
CE
β
VO
βRCRLRB
=VI
(RC+RL+ZO){RBZS+[rbebe+(1+β)ZE]ZS+[rbe+(1+β)ZE]}R
B
R1 || R2 || RS + rbe
1
where Rech = RE ||

f
=
L
<<CC
2πCERech
β
fL =

1
2πCC(RS+R1 || R2 || rbe)
At high frequencies CO, CC and CE behave as short-circuits. Instead, the equivalent capacity Cech given by
the parasitic capacities of the bipolar transistor counts.
The impedances become : ZS = RS, ZE = 0, ZO = 0, and rbe is replaced with Zbe,where :
rbe
Zbe =
1+jωCechrbe
Sugestion: The small signal model of the BJT at high frequencies is presented in Fig.II.3.3.a. Due to
the Miller effect Cbc is multiplied with (1-Av), where Av is the voltage gain. It results the equivalent circuit in
Fig.II.1.3.b. with Cech=Cbe+(1-Av)Cbc.
2
Cbc
B
C

B
Cbe
rb

cech
rb
e
C
e
E
a)
E
b)
Fig. II.3.3. The small signal model of the BT at high frequencies
For the BC190 transistor, at Ic=1,4 mA, consider β=200, Cbe45pF and Cbc2,6pF.
The equivalent circuit will look like the one in Fig.II.3.4.
fH=
Finally it results that:

1
2πCech[RS || (R1 || R2 || rbe)]
How does the frequency response look like? For the frequency, the logaritmic scale will be used.
RS
Vb
VS
Zbe
e
RB
gmVbe
VO
RC || RL
Fig. II.3.4. The equivalent circuit in high frequencies
P2. The effects of the capacities and gain on the frequency bandwidth
We consider Cc=10nF, Ce=100F, Cbc=2,6pF, Av=-90 as reference values.
 Compute fL when CC=47nF, the other quantities being the reference ones, using the relationship:
fL =

Compute fL when CE=1F, the other quantities being the reference ones, using the relationship:
fL=

1
2πCC(RS+R1 || R2 || rbe)
1
2πCERech
,where
Rech = RE ||
R1 || R2 || RS + rbe
β
Compute fH using the relationship:
fH=
1
2πCech[RS || (R1 || R2 || rbe)]
when Cbc=12,6pF, the other quantities being the reference ones.
3

Compute fH when Av=-180, the other quantities being the reference ones.
IV.EXPLORATIONS AND RESULTS
VS=12V
R2
C3
10n
vs
3K3
R4
Co
K2
vo
+
1
Rs
5,6K
82K
Cc K1
2
47n
R3
T
1
0
p
BC190
RL
K3
1
R5
22K
K4
100
2
3K3
+ CE +
1K2
100
1
Fig II.3.5.
1. The dc analysis of the CE amplifier stage
Explorations
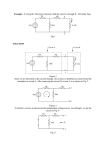
 Build the circuit in Fig. II.3.6. (K1→1, K2→open, K3→1, K4→closed). (See Fig. II.3.7)
 Supply the circuit with 12V dc.
 Measure a minimal number of voltages to determine the bias point of the transistor.
Results
 Give the values of IC and VCE for the transistor.
 Compare the measured IC with the value computed in P.1.
2. The frequency response of the CE amplifier stage
Explorations
We will use the circuit from Fig II.3.6.
 vs is a sine wave from a signal generator, with the amplitude of 40mV and of 5KHz frequency.
 We simultaneously visualize vs(t) and vo(t) with the oscilloscope.
 We adjust, if needed, the amplitude of vs until vo is undistorted.
 We determine the amplitude of vo.
 Without modifying the amplitude of vs we determine the amplitude of vo for the frequencies listed in
Table II.3.1.
Determining fL and fH with the oscilloscope:
 To determine fL: we decrease the frequency of vs until the amplitude of vo decreases to
1
2
the amplitude of vo measured at a frequency of 5kHz.
4
 0.707 from
 To determine fH: we increase vs until the amplitude of vo decreases to
1
 0.707 from the
2
amplitude of vo measured at a frequency of 5kHz.
Vs=12V
R1
82K
R4
3K3
Co
+
vo
CC
v+i
vi
T
100
BC190
RL
10nF
3K3
Ri
+
R2
22K
R5
1K2
CE
100
Fig II.3.6. The BJT amplifier
Results
 Fill in the Table II.3.1.
Table II.3.1
F [Hz]
102
103
5·103
104
105
106
Vo [V]
 The values of fL and fH and of the amplitude of vo at these frequencies. Compare fL and fH with those
computed at P2.
 Fill fL and fH in the first row of Table II.3.2.
 Sketch the Bode plot of the circuit, using your measured values. Compare it with the Bode plots derived
in P.2, and if different, explain why.
3. The effects of the capacitances and of the gain on the bandwidth
Explorations
We want to determine the effects of the capacitors CC, CE, Cbc, and of the voltage gain Av on the amplifier’s
bandwidth. For each of the following variables we consider as reference value: CC=10nF, CE=100F,
Cbe=2,6pF (parasitic capacitance of the transistor), Av=-90 (value which can be determined from the circuit
in Fig II.3.6). We modify these values one at a time, determining each time the bandwidth by measuring fL
and fH, with the oscilloscope, for each of the following situations.
 vs sine wave signal with the amplitude smaller than 40mV
 We visualize vs(t) and vo(t).
 We modify the frequency of vs in order to obtain the maximum amplitude of vo (if vo is distorted we
decrease vs).
1
 We determine fL by decreasing the frequency of vs until the amplitude of vo decreases to
 0.707
2
from the maximum amplitude obtained for vo.
5
 We determine fH by increasing the frequency of vs until the amplitude of vo becomes
1
 0.707 from
2
the maximum amplitude obtained for vo.
a) The CC effect (CC=47nF): K12, K2open, K31, K4closed.
b) The CE effect (CE=1F): K11, K2 open, K32, K4 closed.
c) The Cbe effect: we add a capacitance C=10pF in parallel with Cbe, therefore Cbe=12.6 pF; K11,
K2 closed, K31, K4 closed.
d) The AV effect: K11, K2 open, K31, K4 open.
Results
 For the 4 situations a), b), c), d) mentioned above, we fill in the Table II.3.2 (No.2, 3, 4, 5) the values of
the fL, fH and of the bandwidth B=fH-fL.
Table II.3.2
No.
CC [nF]
CE [F]
Cbe [pF]
(C [pF])
Av
1
10
100
2,6 (0)
-90
2
47
100
2,6 (0)
-90
3
10
1
2,6 (0)
-90
4
10
100
12,6 (10)
-90
5
10
100
2,6 (0)
-180
fL
fH
B
 Compare the measured values (for fL and fH) with those computed at P.2 and P.3.
 Which of the frequencies (fL or fH) modifies its value with respect to each of the 4 variables: CC, CE, Cbe,
Av?
 How do fL and fH modify (increase/decrease) according to the variation of each of the 4 variables? What
combination of values should be chosen for CC, CE, Cbe, Av to obtain: (1) the smallest bandwidth; (2) the
largest bandwidth?
 According to the data from Table II.3.2, which one of the two frequencies: f L or fH, has a greater effect on
the bandwidth? Why?
 If simultaneously CC=47nF and CE=1F, what will be the value of fL?
 If simultaneously Cbc=12,6pF and Av=-180, what will be the value of fH?
6
Alim
VCC
1
2
Rled
5k6
CON2
VCC
LED
LED
J4
CON2
J5
CON2
R4
R2
10n
100n
2
1
5k6
CON2
1
2
1
2
2
100u
J6
2
J7 1
1
2
J10
2
1
1
2
CON2
RL
R5
R3
CON2
3k3
1k2
J8
22k
J14
J16
2
1
2
1
2
1
1
2
47n
J15
Q1
BC107
BC190
2
1
CON2
J3
C2
10p
J2
1
R1
Output
1
2
3
1
2
J9
C4
J1
C1
Input
3k3
C3
1
2
82k
CON2
CON2
CON2
C6
C5
100u
Fig. II.3.7. The experimental assembly
7
1u