* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture 10 slides - Digilent Learn site
Radio transmitter design wikipedia , lookup
Immunity-aware programming wikipedia , lookup
Crystal radio wikipedia , lookup
Topology (electrical circuits) wikipedia , lookup
Electronic engineering wikipedia , lookup
Power electronics wikipedia , lookup
Transistor–transistor logic wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
Surge protector wikipedia , lookup
Power MOSFET wikipedia , lookup
Flexible electronics wikipedia , lookup
Zobel network wikipedia , lookup
Operational amplifier wikipedia , lookup
Schmitt trigger wikipedia , lookup
Index of electronics articles wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Current source wikipedia , lookup
Current mirror wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Integrated circuit wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Regenerative circuit wikipedia , lookup
Opto-isolator wikipedia , lookup
Rectiverter wikipedia , lookup
Two-port network wikipedia , lookup
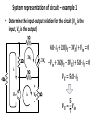
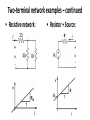
Lecture 10 •Signals and systems •Linear systems and superposition •Thévenin and Norton’s Theorems •Related educational materials: –Chapter 4.1 - 4.5 Review: System representation of circuits • In lecture 1, we claimed that it is often convenient to use a systems-level analysis: • We can define inputs and outputs for a circuit and represent the circuit as a system • The inputs and outputs are, in general, functions of time called signals What’s the difference? • Previously, our circuit analysis has been for a specific input value • Example: Determine the current i System-level approach • Let the voltage source be the “input” and the current the “output” • Represent as system: • Output can be determined for any value of Vin Linear Systems • In lecture 1, we noted that linear systems had linear relations between dependent variables • A more rigorous definition: ax1(t) + S bx2(t) + Linear System ay1(t) + by2(t) Linear system example • Dependent sources are readily analyzed as linear systems: System representation of circuit – example 1 • Determine the input-output relation for the circuit (Vin is the input, VX is the output) 1W 2W i1 3Vx 3W 4W Vin + - i2 + VX - 5W Example 1 – continued • Determine VX if Vin is: (a) 14V (b) 5cos(3t) – 12e-2t Superposition • Special case of linear circuit response: • If a linear circuit has multiple inputs (sources), we can determine the response to each input individually and sum the responses Superposition – continued • Application of superposition to circuit analysis: • Determine the output response to each source • Kill all other sources (short voltage sources, open-circuit current sources) • Analyze resulting circuit to determine response to the one remaining source • Repeat for each source • Sum contributions from all sources Superposition – example 1 • Determine the current i in the circuit below Two-terminal networks • It is sometimes convenient to represent our circuits as two-terminal networks • Allows us to isolate different portions of the circuit • These portions can then be analyzed or designed somewhat independently • Consistent with our systems-level view of circuit analysis • The two-terminal networks characterized by the voltage-current relationship across the terminals • Voltage/current are the input/output of the system Two-terminal networks – examples • Resistor: • Voltage-current relation: • System representations: Two-terminal network examples – continued • Resistive network: • Resistor + Source: Thévenin and Norton’s Theorems • General idea: • We want to replace a complicated circuit with a simple one, such that the load cannot tell the difference • Becomes easier to perform & evaluate load design Thévenin and Norton’s Theorems – continued • We will replace circuit “A” of the previous slide with a simple circuit with the same voltage-current characteristics • Requirements: • Circuit A is linear • Circuit A has no dependent sources controlled by circuit B • Circuit B has no dependent sources controlled by circuit A • Thévenin’s Theorem • Thévenin’s Theorem replaces the linear circuit with a voltage source in series with a resistance • Procedure: Thévenin’s Theorem – continued • • Notes: • This is a general voltage-current relation for a linear, twoterminal network • Voc is the terminal voltage if i = 0 – (the open-circuit voltage) • RTH is the equivalent resistance seen at the terminals (the Thévenin resistance) Creating the Thévenin equivalent circuit 1. Identify and isolate the circuit and terminals for which the Thévenin equivalent circuit is desired 2. Kill the independent sources in circuit and determine the equivalent resistance RTH of the circuit 3. Re-activate the sources and determine the open-circuit voltage VOC across the circuit terminals 4. Place the Thévenin equivalent circuit into the original overall circuit and perform the desired analysis Thévenin’s Theorem – example 1 • Replace everything except the 1A source with its Thévenin equivalent and use the result to find v1 Example 1 – continued