Survey
* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Section 1.6-Classify Polygons
Document related concepts
Anders Johan Lexell wikipedia , lookup
Rational trigonometry wikipedia , lookup
History of trigonometry wikipedia , lookup
Steinitz's theorem wikipedia , lookup
Multilateration wikipedia , lookup
Surface (topology) wikipedia , lookup
Line (geometry) wikipedia , lookup
History of geometry wikipedia , lookup
Regular polytope wikipedia , lookup
Integer triangle wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Shapley–Folkman lemma wikipedia , lookup
Euclidean geometry wikipedia , lookup
Tessellation wikipedia , lookup
Area of a circle wikipedia , lookup
Transcript
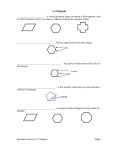
Geometry Section 1.6 - Classify Polygons Objective: SWBAT classify polygons Introduction to Polygons What is a polygon? Is a closed plane figure with the following properties: 1. It is formed by three or more line segments called sides 2. Each side intersects exactly two sides, one at each endpoint, so that no two sides with a common endpoint are collinear. Is it a Polygon? Look at your worksheet… Is it a Polygon? Classify polygons by # sides # sides 3 Name Triangle 4 Quadrilateral 5 Pentagon 6 Hexagon 7 Heptagon Picture Classify polygons by # sides # sides 8 Name Octagon 9 Nonagon 10 Decagon 12 Dodecagon n n-gon Picture Classifying Polygons Convex: a polygon such that no line containing a side of the polygon contains a point in the interior of the polygon Concave: a polygon that is not convex Identify polygon Classifying Polygons Equilateral: a polygon with all sides congruent Equiangular: a polygon with all interior angles congruent. Regular: a convex polygon that is both equilateral and equiangular Classify Polygon Homework Textbook Page 45 # 8-14 (even) # 28 and 30
